The most advanced solver for nonlinear optimization
— Nonlinear optimization problems arise in numerous business and industry applications: portfolio optimization, optimal power flow, nonlinear model predictive control, Nash equilibrium problems. To solve these challenging problems, customers in hundreds of sites worldwide rely on Artelys Knitro for its efficiency and robustness.
Trial license
Get a free trial license of Artelys Knitro to experience the performance, functions, support and services we provide as part of our product offering.
Teaching program
Artelys strongly supports the use of mathematical optimization within academic institutions. We offer free, full-featured copies of Artelys Knitro for teaching purpose.
Purchase Knitro
Discover Artelys Knitro licenses and support services that will help you solve problems and receive solver updates to model optimization problems quickly and easily.
Use-cases
Discover our latest news
Artelys Knitro 15.1: Solve your toughest pooling applications!
Artelys releases Knitro 15.1, bringing a new wave of performance upgrades and usability improvements to help you solve large-scale optimization problems faster than ever.
Discover our latest news
Artelys Knitro 15.1: Solve your toughest pooling applications!
Artelys releases Knitro 15.1, bringing a new wave of performance upgrades and usability improvements to help you solve large-scale optimization problems faster than ever.
— More than 450 institutions in over 40 countries rely on Artelys Knitro.
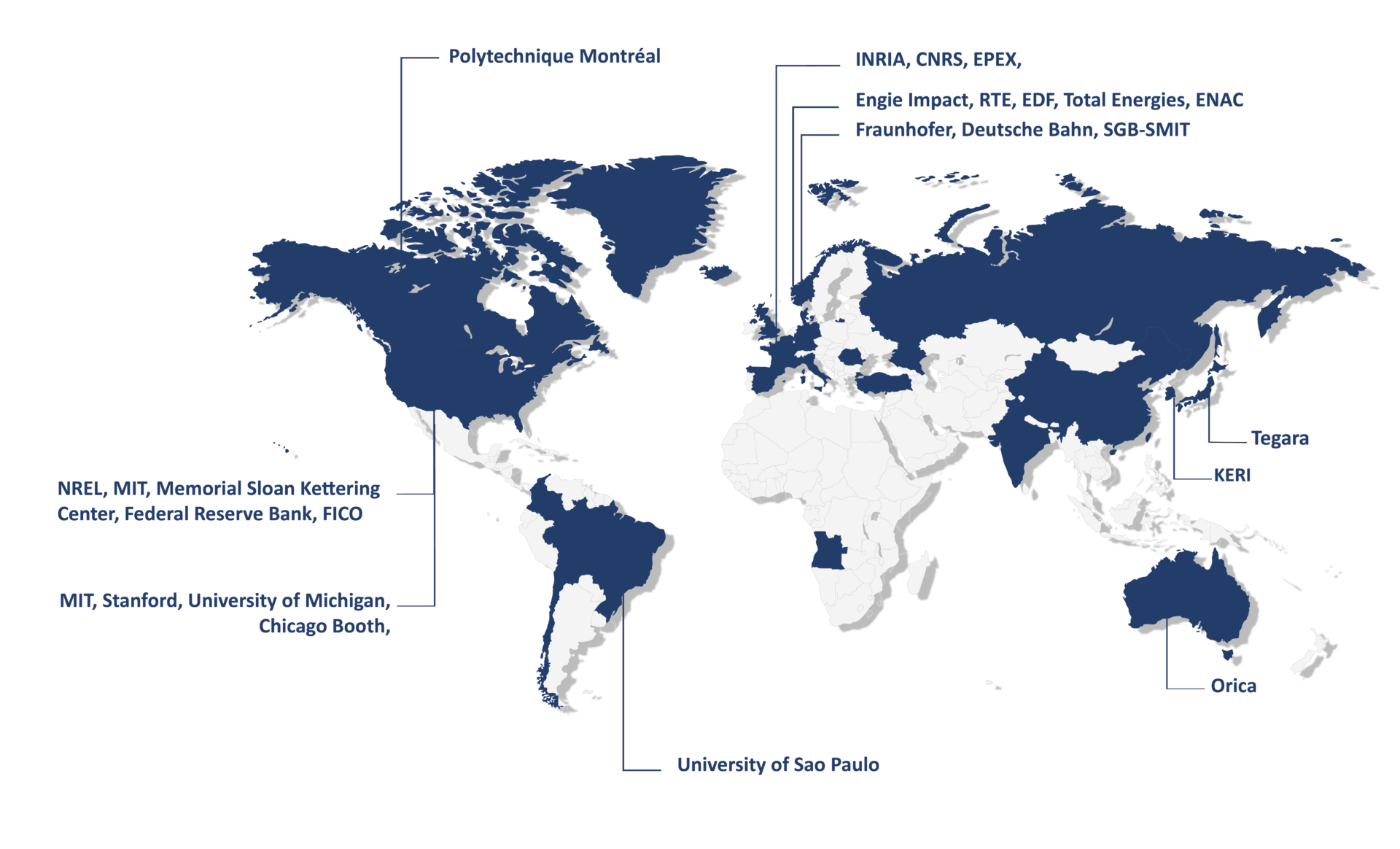

countries
institutions
algorithms
interfaces
Solve all your optimization problems

— With 7 algorithms, and several key features, Artelys Knitro can efficiently solve a wide range of optimization problems.
Efficient and robust solution on large scale problems
Two interior-point/barrier and two active-set/SQP algorithms
Three algorithms for mixed-integer nonlinear optimization
Heuristics, cutting planes, branching rules for MINLP
Special routine to handle complementarity constraints
Parallel multistart feature for global optimization
Ability to run multiple algorithms concurrently
Automatic and parallel tuning of option settings
Automatic computation of approximate first-order and second-order derivatives
Smart initialization strategies and fast infeasibility detection
Interfaces


Artelys Knitro is supported on Windows, Linux and Mac distribution.
Complete list: see our documentation.
— “Artelys Knitro and AMPL performance enables the automation of radiation therapy cancer treatment, resulting in faster treatment delivery and more accurate tumor irradiation and healthy tissue sparing. Thanks to the resolution of complex large scale optimization models more than 800 patients were treated since the beginning of the project.”
— “The use of robust, innovative and powerful components enables us to carry out reliable analyses about sensitive issues such as network security.”
— “Our software incorporates Knitro to solve very complex mixed integer nonlinear programming (MINLP) optimization problems. These problems must be solved in near-real time (at the 5 minute level), and we have found no other solver that matches the speed and accuracy of Knitro. In addition, the customer support at Artelys has been fantastic. They have been very responsive to our needs, have worked closely with us in product development, and have been very flexible in product implementation and licensing.”
Request demo
© ARTELYS • All rights reserved • Legal mentions