Frequency assignment¶
The area of telecommunications, and in particular mobile telecommunications, gives rise to many different variants of frequency assignment problems. We are given a network of cells (nodes) with requirements of discrete frequency bands. Each cell has a given demand for a number of frequencies (bands). Figure 11.2.1 shows the structure of the network. Nodes linked by an edge are considered as neighbors. They must not be assigned the same frequencies to avoid interference. Furthermore, if a cell uses several frequencies they must all be different by at least 2. The objective is to minimize the total number of frequencies used in the network.
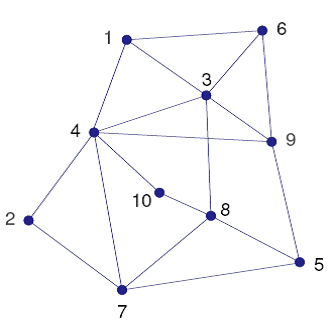
Fig. 25 Telecommunications network¶
The following table lists the number of frequency demands for every cell:
Cell |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Demand |
4 |
5 |
2 |
3 |
2 |
4 |
3 |
4 |
3 |
2 |
Model formulation¶
Let  be the set of all nodes in the network and
be the set of all nodes in the network and  the demand of frequencies at node
the demand of frequencies at node  . The network is given as a set of edges
. The network is given as a set of edges  . Furthermore, let
. Furthermore, let 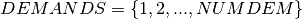 be the set of frequencies, numbered consecutively across all nodes where the upper bound
be the set of frequencies, numbered consecutively across all nodes where the upper bound 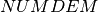 is given by the total number of demands. The auxiliary array
is given by the total number of demands. The auxiliary array 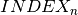 indicates the starting index in
indicates the starting index in 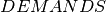 for node
for node 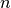 . For representing the frequency assigned to every demand
. For representing the frequency assigned to every demand 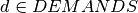 we introduce the variables
we introduce the variables 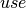 that take their values from the set
that take their values from the set 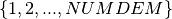 . The two sets of constraints (different frequencies assigned to neighboring nodes and minimum distance between frequencies within a node) can then be modeled as follows.
. The two sets of constraints (different frequencies assigned to neighboring nodes and minimum distance between frequencies within a node) can then be modeled as follows.

The objective function is to minimize to the number of frequencies used. We formulate this by minimizing the largest frequency number that occurs for the 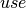 variables:
variables:
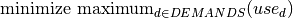
Implementation¶
The edges forming the telecommunications network are modeled as a list 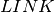 , where edge
, where edge 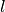 is given as
is given as 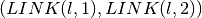 . For the implementation of the constraints on the values of frequencies assigned to the same node we have two equivalent choices with Kalis, namely using
. For the implementation of the constraints on the values of frequencies assigned to the same node we have two equivalent choices with Kalis, namely using abs or distance constraints.
const int NODES = 10;
// Range of links between nodes
const int LINKS = 18 ;
// Demand of nodes
int DEM[] = {4, 5, 2, 3, 2, 4, 3, 4, 3, 2};
// Neighboring nodes
int LINK[18][2] = {{1, 3}, {1, 4}, {1, 6},{2, 4}, {2, 7},{3, 4}, {3, 6}, {3, 8}, {3, 9},{4, 7}, {4, 9}, {4,10},{5, 7}, {5, 8}, {5, 9},{6, 9}, {7, 8}, {8,10}};
// Start index in 'use'
int INDEX[10];
// Upper bound on no. of freq.
int NUMDEM;
int n;
NUMDEM = 0;
for (n=0;n<NODES;n++) {
NUMDEM += DEM[n];
}
// Correspondence of nodes and demand indices:
// use[d] d = 0, ..., DEM[1] correspond to the demands of node 0
// d = DEM[0]+1, ..., DEM[0]+DEM(1)) - " - node 2 etc.
INDEX[0] = 0;
for (n=1;n<NODES;n++) {
INDEX[n] = INDEX[n-1] + DEM[n-1];
}
// Creation of the problem in this session
KProblem problem(session,"Frequency assignment");
char name[80];
// Frequency used for a demand
KIntVarArray use;
int d,c;
for (d=0;d<NUMDEM;d++) {
sprintf(name,"use(%i)",d);
use += (* new KIntVar(problem,name,1,NUMDEM) );
}
KIntVar numfreq(problem,"numfreq",0,LINKS);
// All frequencies attached to a node must be different by at least 2
for (n=0;n<NODES;n++) {
for (c=INDEX[n];c<= INDEX[n] + DEM[n] - 1;c++) {
for (d=INDEX[n];d<= INDEX[n] + DEM[n] - 1;d++) {
if (c < d) {
problem.post(KDistanceGreaterThanXyc(use[c],use[d],2));
}
}
}
}
// Neighboring nodes take all-different frequencies
int l;
for (l=0;l<LINKS;l++) {
KIntVarArray diff;
for (d=INDEX[LINK[l][0]-1];d <= INDEX[LINK[l][0]-1] + DEM[LINK[l][0]-1]-1 ;d++) {
diff += use[d];
}
for (d=INDEX[LINK[l][1]-1];d <= INDEX[LINK[l][1]-1] + DEM[LINK[l][1]-1]-1 ;d++) {
diff += use[d];
}
problem.post(KAllDifferent("diff",diff,KAllDifferent::USING_GCC));
}
// Objective function: minimize the number of frequencies used, that is
//minimize the largest value assigned to 'use'
problem.post(KMax("maxuse",numfreq,use,false));
// propagating problem
if (problem.propagate()) {
printf("Problem is infeasible\n");
exit(1);
}
// Search strategy
KBranchingSchemeArray myBa;
myBa += KAssignVar(KSmallestDomain(),KMinToMax(),use);
// Solve the problem
// creation of the solver
KSolver solver(problem,myBa);
solver.setDblControl(KSolver::MaxComputationTime,1.0);
solver.setSolutionFunctionPtr(solution_found,&problem);
// Try to find solution(s) with strategy 1
problem.setSense(KProblem::Minimize);
problem.setObjective(numfreq);
int nsol = -1;
if (solver.optimize()) {
solver.printStats();
KSolution * sol = &problem.getSolution();
nsol = sol->getObjectiveValue();
numfreq.setSup(nsol-1);
}
printf("Number of frequencies: %f\n", problem.getSolution().getObjectiveValue());
printf("Frequency assignment: \n");
for (n=0;n<NODES;n++) {
printf("Node %i: ",n);
for (d=INDEX[n];d<=INDEX[n]+DEM[n]-1;d++) {
printf("%i ",problem.getSolution().getValue(use[d]));
}
printf("\n");
}
// Search strategy
KBranchingSchemeArray myBa2;
myBa2 += KAssignVar(KMaxDegree(),KMinToMax(),use);
// Solve the problem
// creation of the solver
KSolver solver2(problem,myBa2);
solver2.setSolutionFunctionPtr(solution_found,&problem);
// Try to find solution(s) with strategy 2
if (solver2.optimize()) {
solver2.printStats();
KSolution * sol = &problem.getSolution();
}
printf("Number of frequencies: %f\n", problem.getSolution().getObjectiveValue());
printf("Frequency assignment: \n");
for (n=0;n<NODES;n++) {
printf("Node %i: ",n);
for (d=INDEX[n];d<=INDEX[n]+DEM[n]-1;d++) {
printf("%i ",problem.getSolution().getValue(use[d]));
}
printf("\n");
}
import sys
from kalis import *
### Data creation
# Demand of nodes
nodes_demands = [4, 5, 2, 3, 2, 4, 3, 4, 3, 2]
# Neighboring nodes
links = [(1, 3), (1, 4), (1, 6),(2, 4), (2, 7),(3, 4), (3, 6), (3, 8), (3, 9),(4, 7), (4, 9), (4,10),(5, 7), (5, 8), (5, 9),(6, 9), (7, 8), (8,10)]
# Set upper bound and total demand
nb_demands = sum(nodes_demands)
nb_nodes = len(nodes_demands)
nb_links = len(links)
# Correspondance between demands and nodes
demands_index = [0]
for n in range(1, nb_nodes):
demands_index.append(demands_index[n-1] + nodes_demands[n-1])
### Creation of the problem
# Creation of the Kalis session
session = KSession()
# Creation of the optimization problem
problem = KProblem(session, "Frequency assignment")
### Creation of the variables
# One variable for each demand representing the id of the given frequency
use = KIntVarArray()
for d in range(nb_demands):
use += KIntVar(problem, "use(%d)" % n, 1, nb_demands)
# Variable for the objective value:
nb_of_frequencies = KIntVar(problem, 'nb of frequencies', 0, nb_links)
### Creation of the constraints
# All frequencies attached to a node must be different by at least 2
for n in range(nb_nodes):
for d1 in range(demands_index[n], demands_index[n] + nodes_demands[n]):
for d2 in range(d1 + 1, demands_index[n] + nodes_demands[n]):
problem.post(KDistanceGreaterThanXyc(use[d1], use[d2], 2))
# Neighboring nodes take all-different frequencies
for l in links:
diff = KIntVarArray()
# Add all first link node frequencies demands
n1 = l[0] - 1
for d in range(demands_index[n1], demands_index[n1] + nodes_demands[n1]):
diff += use[d]
n2 = l[1] - 1
for d in range(demands_index[n2], demands_index[n2] + nodes_demands[n2]):
diff += use[d]
problem.post(KAllDifferent("diff", diff, KAllDifferent.USING_GCC))
# Objective function: minimize the number of used frequencies, that is minimize the largest
# value assigned in the 'use' array.
problem.post(KMax("maxuse", nb_of_frequencies, use, False))
# Propagate the problem
if problem.propagate():
print("Problem is infeasible")
sys.exit(1)
# Set the search strategy
my_branching_array = KBranchingSchemeArray()
my_branching_array += KAssignVar(KSmallestDomain(), KMinToMax(), use)
### Solve the problem
# Set callback to print solution when a new one is found
class SolutionListener(KSolverEventListener):
def __init__(self, problem):
KSolverEventListener.__init__(self, problem)
def solutionFound(self, solution, thread_id):
solution.printResume()
# creation of the solver
solver = KSolver(problem, my_branching_array)
solver.setDblControl(KSolver.MaxComputationTime, 1.0)
solver.setSolverEventListener(SolutionListener(problem))
# Try to find solution with a first strategy
problem.setSense(KProblem.Minimize)
problem.setObjective(nb_of_frequencies)
nb_of_used_frequencies = -1
if solver.optimize():
solver.printStats()
solution = problem.getSolution()
nb_of_used_frequencies = solution.getObjectiveValue()
nb_of_frequencies.setSup(int(nb_of_used_frequencies) - 1)
print("Number of frequencies: %d" % problem.getSolution().getObjectiveValue())
print("Frequency assignment:")
for n in range(nb_nodes):
print("Node %d: " % (n + 1), end='')
for d in range(demands_index[n], demands_index[n] + nodes_demands[n]):
print("%d " % problem.getSolution().getValue(use[d]), end='')
print("")
# Try to find solution with a second strategy
my_branching_array2 = KBranchingSchemeArray()
my_branching_array2 += KAssignVar(KMaxDegree(), KMinToMax(), use)
solver2 = KSolver(problem, my_branching_array2)
if solver2.optimize():
solver2.printStats()
solution = problem.getSolution()
print("Number of frequencies: %d" % solution.getObjectiveValue())
print("Frequency assignment:")
for n in range(nb_nodes):
print("Node %d: " % (n + 1), end='')
for d in range(demands_index[n], demands_index[n] + nodes_demands[n]):
print("%d " % problem.getSolution().getValue(use[d]), end='')
print("")
int NODES = 10;
// Range of links between nodes
int LINKS = 18 ;
// Demand of nodes
int[] DEM = {4, 5, 2, 3, 2, 4, 3, 4, 3, 2};
// Neighboring nodes
int[][] LINK = {{1, 3}, {1, 4}, {1, 6},{2, 4}, {2, 7},{3, 4}, {3, 6}, {3, 8}, {3, 9},{4, 7}, {4, 9}, {4,10},{5, 7}, {5, 8}, {5, 9},{6, 9}, {7, 8}, {8,10}};
// Start index in 'use'
int[] INDEX = new int[NODES];
// Upper bound on no. of freq.
int NUMDEM;
System.loadLibrary("KalisJava");
try {
NUMDEM = 0;
int indexNode;
for (indexNode=0; indexNode < NODES; indexNode++)
{
NUMDEM += DEM[indexNode];
}
// Correspondence of nodes and demand indices:
// use[d] d = 0, ..., DEM[1] correspond to the demands of node 0
// d = DEM[0]+1, ..., DEM[0]+DEM(1)) - " - node 2 etc.
INDEX[0] = 0;
for (indexNode=1;indexNode<NODES;indexNode++)
{
INDEX[indexNode] = INDEX[indexNode-1] + DEM[indexNode-1];
}
KSession session = new KSession();
// Creation of the problem in this session
KProblem problem = new KProblem(session,"Frequency assignment");
// Frequency used for a demand
KIntVarArray use = new KIntVarArray();
int d,c;
for (d=0;d<NUMDEM;d++) {
use.add(new KIntVar(problem,"use("+d+")",1,NUMDEM) );
}
KIntVar numfreq = new KIntVar(problem,"numfreq",0,LINKS);
// All frequencies attached to a node must be different by at least 2
for (indexNode=0; indexNode<NODES; indexNode++) {
for (c=INDEX[indexNode];c<= INDEX[indexNode] + DEM[indexNode] - 1;c++) {
for (d=INDEX[indexNode];d<= INDEX[indexNode] + DEM[indexNode] - 1;d++) {
if (c < d) {
problem.post(new KDistanceGreaterThanXyc(use.getElt(c),use.getElt(d),2));
}
}
}
}
// Neighboring nodes take all-different frequencies
int l;
for (l=0;l<LINKS;l++) {
KIntVarArray diff = new KIntVarArray();
for (d=INDEX[LINK[l][0]-1];d <= INDEX[LINK[l][0]-1] + DEM[LINK[l][0]-1]-1 ;d++) {
diff.add(use.getElt(d));
}
for (d=INDEX[LINK[l][1]-1];d <= INDEX[LINK[l][1]-1] + DEM[LINK[l][1]-1]-1 ;d++) {
diff.add(use.getElt(d));
}
problem.post(new KAllDifferent("diff",diff,KAllDifferent.PropagationLevel.USING_GCC));
}
// Objective function: minimize the number of frequencies used, that is
//minimize the largest value assigned to 'use'
problem.post(new KMax("maxuse",numfreq,use,false));
// propagating problem
if (problem.propagate()) {
System.out.println("Problem is infeasible");
exit(1);
}
// Search strategy
KBranchingSchemeArray myBa = new KBranchingSchemeArray();
myBa.add(new KAssignVar(new KSmallestDomain(),new KMinToMax(),use));
// Solve the problem
// creation of the solver
KSolver solver = new KSolver(problem,myBa);
solver.setDblControl(KSolver.DblControl.MaxComputationTime,1.0);
// Try to find solution(s) with strategy 1
problem.setSense(KProblem.Sense.Minimize);
problem.setObjective(numfreq);
int nsol = -1;
if (solver.optimize() > 0)
{
solver.printStats();
KSolution sol = problem.getSolution();
nsol = (int) sol.getObjectiveValue();
numfreq.setSup(nsol - 1);
}
System.out.println("Number of frequencies: " + problem.getSolution().getObjectiveValue());
System.out.println("Frequency assignment: ");
for (indexNode=0; indexNode<NODES; indexNode++) {
System.out.println("Node " + indexNode);
for (d=INDEX[indexNode]; d<=INDEX[indexNode]+DEM[indexNode]-1;d++) {
System.out.println(problem.getSolution().getValue(use.getElt(d)));
}
}
// Search strategy
KBranchingSchemeArray myBa2 = new KBranchingSchemeArray();
myBa2.add(new KAssignVar(new KMaxDegree(), new KMinToMax(), use));
// Solve the problem
// creation of the solver
KSolver solver2 = new KSolver(problem,myBa2);
// Try to find solution(s) with strategy 2
if (solver2.optimize() > 0) {
solver2.printStats();
KSolution sol = problem.getSolution();
}
System.out.println("Number of frequencies: " + problem.getSolution().getObjectiveValue());
System.out.println("Frequency assignment: ");
for (indexNode=0; indexNode<NODES; indexNode++)
{
System.out.println("Node " + indexNode);
for (d = INDEX[indexNode]; d <= INDEX[indexNode] + DEM[indexNode] - 1; d++)
{
System.out.println(problem.getSolution().getValue(use.getElt(d)));
}
}
} catch (Exception e)
{
e.printStackTrace();
}
With just the default search strategy this model finds a solution of value 11 but it runs for a long time without being able to prove optimality. When experimenting with different search strategies we have found that the strategy obtained by changing the variable selection criterion to KMaxDegree is able to prove optimality easily once a good solution is known. This problem is therefore solved in two steps: First, we use the default strategy for finding a good solution. This search is stopped after one second by setting a time limit. The search is then restarted with a second strategy and the bound on the objective value from the previous run. Another new feature demonstrated by this implementation is the use of a callback, more precisely the solution callback of Artelys Kalis. The solution callback is defined with a user subroutine that will be called by the solver whenever the search has found a solution. Its typical uses are logging or storing of intermediate solutions or performing some statistics. Our procedure solution_found() simply prints out the solution that has been found.
int solution_found(void *param) {
KProblem * p = (KProblem *) param;
p->getSolution().printResume();
return 0;
}
class SolutionListener(KSolverEventListener):
def __init__(self, problem):
KSolverEventListener.__init__(self, problem)
def solutionFound(self, solution, thread_id):
solution.printResume()
class MySolverEventListener extends KSolverEventListener
{
public void nodeExplored() {
System.out.println("Node explored");
}
public void branchGoDown() {
System.out.println("Branch go down");
}
public void branchGoUp() {
System.out.println("Branch go up");
}
public void branchingScheme() {
}
public boolean stopComputations() {
return false;
}
public void solutionFound() {
System.out.println("A solution has been found!");
}
}
Improving the problem formulation¶
We may observe that in our problem formulation all demand variables within a node and the constraints on these variables are entirely symmetric. In the absence of other constraints, we may reduce these symmetries by imposing an order on the 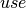 variables,
variables, 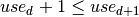 for demands
for demands 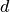 and
and 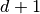 belonging to the same cell. Doing so, the problem is solved to optimality within less than 40 nodes using just the default strategy. We may take this a step further by writing:
belonging to the same cell. Doing so, the problem is solved to optimality within less than 40 nodes using just the default strategy. We may take this a step further by writing: 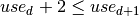 . The addition of these constraints shortens the search by yet a few more nodes. They can even be used simply in replacement of the
. The addition of these constraints shortens the search by yet a few more nodes. They can even be used simply in replacement of the abs or distance constraints.
