Assignment with allowed groups¶
Problem description¶
Let us consider now an assignment problem in which only certain allowed groups of workers can be assigned to the tasks. Let derive directly an example here.
Consider there are twelve workers, numbered  -
-  . The allowed groups are combinations of the following pairs of workers.
. The allowed groups are combinations of the following pairs of workers.
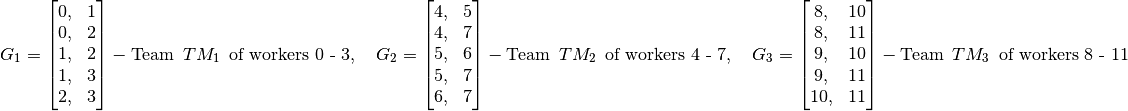
An allowed group can be any combination of three pairs of workers, one pair from each of 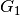 ,
, 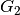 , and
, and  .
.
For example, combining [2, 3], [6, 7], and [10, 11] results in the allowed group [2, 3, 6, 7, 10, 11].
Since each of the three sets contains five elements, the total number of allowed groups is 5 * 5 * 5 = 125.
To model this constraint, we would like to introduce a constraint GAC (Generalized Arc Consistency) in a table version. It means that we would like to define all combinations within a table, and add a constraint over the variables to be part of one of the combination.
More precisely, for the team 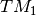 we will introduce variables
we will introduce variables 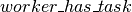 to be able to know if a task is perform by the worker. Then,
to be able to know if a task is perform by the worker. Then, 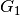 constraint can be expressed :
constraint can be expressed :
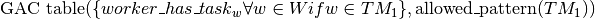
with
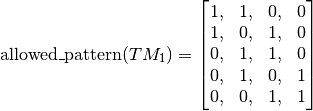
Implementation with a GAC constraint¶
This is a non-convex problem and the constraint ‘only some pair of workers are allowed to work together’ can be difficult to implement. In the first version, the
Kalis class KGeneralizedArcConsistencyConstraint is used to create a ValidTeamPattern class by overloading the testIfSatisfied method to make it
check wether the worker assigned to some tasks are actually allowed.
This implementation can be done as follows:
class ValidTeamPattern(KGeneralizedArcConsistencyConstraint): """This class ineherits from the KACBinConstraint and allow to define a custom binary arc-consistency constraint.""" def __init__(self, vars, valid_combination): """Initialize the StartingTimeCombinationGAC constraint.""" KGeneralizedArcConsistencyConstraint.__init__(self, vars, KGeneralizedArcConsistencyConstraint.GENERALIZED_ARC_CONSISTENCY, "StartingTimeCombinationGAC") self.vars = vars self.valid_combination = valid_combination def testIfSatisfied(self, values): """Overload the 'testIfSatisfied' method in 'KGeneralizedArcConsistencyConstraint' class by using a user defined function. """ return list(values) in self.valid_combination def allowed_pattern(allowed_groups_team: list, teams_worker: list) -> list: """ Creation of an array summing up the allowed groups from a team. The output has the following format : [[0, 1, 0, 1], [1, 0, 0, 1]] In this example, the first line allows the second and fourth workers to work together and the second line allows the first and fourth workers to work together. """ res = [] for group in allowed_groups_team: combination = [] for worker in teams_worker: combination += [1] if worker in group else [0] res += [combination] return res def solve(cost_matrix: list, allowed_groups: list): # Get the number of tasks and workers from the cost matrix nb_worker = len(cost_matrix) nb_task = len(cost_matrix[1]) # Get the number of groups from the allowed_groups array nb_teams = len(allowed_groups) # Get the composition of the teams from the allowed_groups array teams_worker = [] for team in range(nb_teams): teams_worker += [[]] for pair in allowed_groups[team]: for worker in pair: if worker not in teams_worker[team]: teams_worker[team] += [worker] try: # Declaration of the problem session = KSession() problem = KProblem(session, "allowed_groups") # Variable declaration # Declaration of a binary variable for each task/worker combination, stating whether the task has been assigned # to the worker worker_has_task = {} for worker in range(nb_worker): worker_has_task[worker] = KIntVarArray() for task in range(nb_task): worker_has_task[worker] += KIntVar(problem, "Worker_{}_Task_{}".format(worker, task), 0, 1) # Constraint declaration # Ensure that each task is assigned once for task in range(nb_task): problem.post(sum(worker_has_task[worker][task] for worker in range(nb_worker)) == 1) # Ensure that the selected workers from each team are allowed to work together # First a variable counting the number of tasks allocated to each worker is created. Those variables are binary, # thus ensuring that every worker has one tasks at most nb_task_worker = KIntVarArray() for worker in range(nb_worker): nb_task_worker += KIntVar(problem, "Nb_task_worker_{}".format(worker), 0, 1) problem.post(nb_task_worker[worker] == sum(worker_has_task[worker][task] for task in range(nb_task))) # Post the allowed group constraint patterns = {} allowed = {} for team in range(nb_teams): patterns[team] = KIntVarArray() for worker in teams_worker[team]: patterns[team] += nb_task_worker[worker] allowed_pattern_array = allowed_pattern(allowed_groups[team], teams_worker[team]) allowed[team] = ValidTeamPattern(patterns[team], allowed_pattern_array) problem.post(allowed[team]) # Objective declaration # The objective will be greater than nb_task * the minimum of cost_matrix and lower than the sum of the # coefficients in cost_matrix objective_sup = sum(cost_matrix[worker][task] for task in range(nb_task) for worker in range(nb_worker)) objective_inf = nb_task * min( cost_matrix[worker][task] for task in range(nb_task) for worker in range(nb_worker)) # The objective is the sum of the costs objective = KIntVar(problem, "cost", objective_inf, objective_sup) problem.post(objective == sum(cost_matrix[worker][task] * worker_has_task[worker][task] for task in range(nb_task) for worker in range(nb_worker))) # Set the objective problem.setSense(KProblem.Minimize) problem.setObjective(objective) # Set the solver solver = KSolver(problem) # If the problem is infeasible if problem.propagate(): # Display of various details to help find the source of the problem problem.display() problem.printMinimalConflictSet() print("Problem is infeasible") exit() # Launch the optimization result = solver.optimize() if result: solution = problem.getSolution() # Display the solution for task in range(nb_task): for worker in range(nb_worker): if solution.getValue(worker_has_task[worker][task]) == 1: print( f'Task {task} has been affected to worker {worker} 'f'with cost {cost_matrix[worker][task]}') print(f'Total cost : {solution.getValue(objective)}') # Return the objective problem.getSolution().display() return solution.getValue(objective) except ArtelysException as e: print(e) if __name__ == '__main__': COST = [[90, 76, 75, 70, 50, 74], [35, 85, 55, 65, 48, 101], [125, 95, 90, 105, 59, 120], [45, 110, 95, 115, 104, 83], [60, 105, 80, 75, 59, 62], [45, 65, 110, 95, 47, 31], [38, 51, 107, 41, 69, 99], [47, 85, 57, 71, 92, 77], [39, 63, 97, 49, 118, 56], [47, 101, 71, 60, 88, 109], [17, 39, 103, 64, 61, 92], [101, 45, 83, 59, 92, 27]] ALLOWED_GROUPS = [[[2, 3], [1, 3], [1, 2], [0, 1], [0, 2]], [[6, 7], [5, 7], [5, 6], [4, 5], [4, 7]], [[10, 11], [9, 11], [9, 10], [8, 10], [8, 11]]] solve(COST, ALLOWED_GROUPS)
Implementation with a GAC table constraint¶
The GAC method implemented above shows how any constraint can be implemented simply by overloading the testIfSatisfied method. However,
the KGeneralizedArcConsistencyTableConstraint class already implemented in Kalis is precisely made to ensure that the value taken by a set
of variable is equal to one of the sets of variables present in a tuple.
A way to implement this method is as follows :
def allowed_pattern(allowed_groups_team: list, teams_worker: list) -> KTupleArray: """ Creation of an array summing up the allowed groups from a team. The output has the following format : [[0, 1, 0, 1], [1, 0, 0, 1]] In this example, the first line allows the second and fourth workers to work together and the second line allows the first and fourth workers to work together. """ res = KTupleArray() for group in allowed_groups_team: combination = KIntArray() for worker in teams_worker: combination += 1 if worker in group else 0 res += combination res.display() return res def solve(cost_matrix: list, allowed_groups: list): # Get the number of tasks and workers from the cost matrix nb_worker = len(cost_matrix) nb_task = len(cost_matrix[1]) # Get the number of groups from the allowed_groups array nb_teams = len(allowed_groups) # Get the composition of the teams from the allowed_groups array teams_worker = [] for team in range(nb_teams): teams_worker += [[]] for pair in allowed_groups[team]: for worker in pair: if worker not in teams_worker[team]: teams_worker[team] += [worker] try: # Declaration of the problem session = KSession() problem = KProblem(session, "allowed_groups") # Variable declaration # Declaration of a binary variable for each task/worker combination, stating wether the task has been assigned # to the worker worker_has_task = {} for worker in range(nb_worker): worker_has_task[worker] = KIntVarArray() for task in range(nb_task): worker_has_task[worker] += KIntVar(problem, "Worker_{}_Task_{}".format(worker, task), 0, 1) # Constraint declaration # Ensure that each task is assigned once for task in range(nb_task): problem.post(sum(worker_has_task[worker][task] for worker in range(nb_worker)) == 1) # Ensure that the selected workers from each team are allowed to work together # First a variable counting the number of tasks allocated to each worker is created. Those variables are binary, # thus ensuring that every worker has one tasks at most nb_task_worker = KIntVarArray() for worker in range(nb_worker): nb_task_worker += KIntVar(problem, "Nb_task_worker_{}".format(worker), 0, 1) problem.post(nb_task_worker[worker] == sum(worker_has_task[worker][task] for task in range(nb_task))) # Post the allowed group constraint patterns = {} allowed = {} for team in range(nb_teams): patterns[team] = KIntVarArray() for worker in teams_worker[team]: patterns[team] += nb_task_worker[worker] allowed_pattern_array = allowed_pattern(allowed_groups[team], teams_worker[team]) allowed[team] = KGeneralizedArcConsistencyTableConstraint(patterns[team], allowed_pattern_array, "Pair_team_{}".format(team)) problem.post(allowed[team]) # Objective declaration # The objective will be greater than nb_task * the minimum of cost_matrix and lower than the sum of the # coefficients in cost_matrix objective_sup = sum(cost_matrix[worker][task] for task in range(nb_task) for worker in range(nb_worker)) objective_inf = nb_task * min( cost_matrix[worker][task] for task in range(nb_task) for worker in range(nb_worker)) # The objective is the sum of the costs objective = KIntVar(problem, "cost", objective_inf, objective_sup) problem.post(objective == sum(cost_matrix[worker][task] * worker_has_task[worker][task] for task in range(nb_task) for worker in range(nb_worker))) # Set the objective problem.setSense(KProblem.Minimize) problem.setObjective(objective) # Set the solver solver = KSolver(problem) # If the problem is infeasible if problem.propagate(): # Display of various details to help find the source of the problem problem.display() problem.printMinimalConflictSet() print("Problem is infeasible") exit() # Launch the optimization result = solver.optimize() print("end result") if result: solution = problem.getSolution() # Display the solution for task in range(nb_task): for worker in range(nb_worker): if solution.getValue(worker_has_task[worker][task]) == 1: print( f'Task {task} has been affected to worker {worker} 'f'with cost {cost_matrix[worker][task]}') print(f'Total cost : {solution.getValue(objective)}') # Return the objective problem.getSolution().display() return solution.getValue(objective) except ArtelysException as e: print(e) if __name__ == '__main__': COST = [[90, 76, 75, 70, 50, 74], [35, 85, 55, 65, 48, 101], [125, 95, 90, 105, 59, 120], [45, 110, 95, 115, 104, 83], [60, 105, 80, 75, 59, 62], [45, 65, 110, 95, 47, 31], [38, 51, 107, 41, 69, 99], [47, 85, 57, 71, 92, 77], [39, 63, 97, 49, 118, 56], [47, 101, 71, 60, 88, 109], [17, 39, 103, 64, 61, 92], [101, 45, 83, 59, 92, 27]] ALLOWED_GROUPS = [[[2, 3], [1, 3], [1, 2], [0, 1], [0, 2]], [[6, 7], [5, 7], [5, 6], [4, 5], [4, 7]], [[10, 11], [9, 11], [9, 10], [8, 10], [8, 11]]] solve(COST, ALLOWED_GROUPS)