Sudoku¶
Sudoku puzzles, originating from Japan, have recently made their appearance in many western newspapers. The idea of these puzzles is to complete a given, partially filled 9 × 9 board with the numbers 1 to 9 in such a way that no line, column, or 3 × 3 subsquare contains a number more than once. The figures Fig. 22 and Fig. 23 show two instances of such puzzles. Whilst sometimes tricky to solve for a human, these puzzles lend themselves to solving by a constraint programming approach.
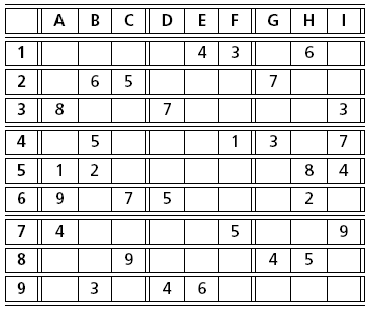
Fig. 22 Sudoku (‘The Times’, 26 January, 2005)¶
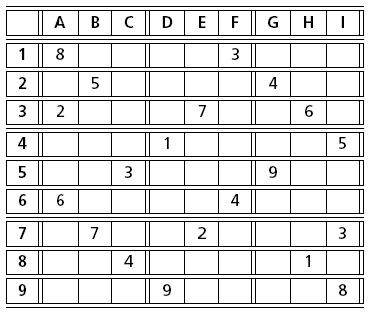
Fig. 23 Sudoku (‘The Guardian’, 29 July, 2005)¶
Model formulation¶
As in the examples, we denote the columns of the board by the set 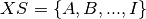 and the rows by
and the rows by 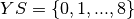 . For every
. For every 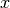 in
in 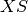 and
and 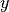 in
in 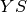 we define a decision variable
we define a decision variable 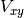 taking as its value the number at the position
taking as its value the number at the position 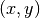 .
.
The only constraints in this problem are:
all numbers in a row must be different,
all numbers in a column must be different,
all numbers in a 3 × 3 subsquare must be different.
These constraints can be stated with the KAllDifferent constraint that ensures that all variables in the relation take different values (see definition here).
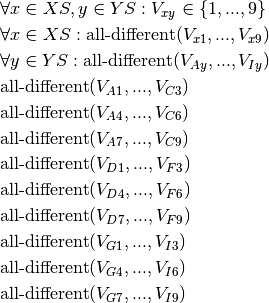
In addition, certain variables 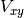 are fixed to the given values.
are fixed to the given values.
Implementation¶
The implementation for the Sudoku puzzle in figure Fig. 23 looks as follows:
// index variables
int indexX,indexY;
// Creation of the problem in this session
KProblem problem(session,"Sudoku");
// creation of a 9x9 matrix of KintVar
// we use the following bijection: A,B,..,I <-> 0,1,..,8
char name[80];
KIntVar *** vars = new KIntVar **[9];
for (indexX = 0;indexX < 9 ; indexX++)
{
vars[indexX] = new KIntVar * [9];
for (indexY = 0;indexY < 9 ; indexY++)
{
sprintf(name,"v[%i,%i]",indexX,indexY);
vars[indexX][indexY] = new KIntVar(problem,name,1,9);
}
}
// Data from "The Guardian", 29 July, 2005. http://www.guardian.co.uk/sudoku
vars[0][0]->instantiate(8); vars[5][0]->instantiate(3);
vars[1][1]->instantiate(5); vars[6][1]->instantiate(4);
vars[0][2]->instantiate(2); vars[4][2]->instantiate(7); vars[7][2]->instantiate(6);
vars[3][3]->instantiate(1); vars[8][3]->instantiate(5);
vars[2][4]->instantiate(3); vars[6][4]->instantiate(9);
vars[0][5]->instantiate(6); vars[5][5]->instantiate(4);
vars[1][6]->instantiate(7); vars[4][6]->instantiate(2); vars[8][6]->instantiate(3);
vars[2][7]->instantiate(4); vars[7][7]->instantiate(1);
vars[3][8]->instantiate(9); vars[8][8]->instantiate(8);
// All-different values in rows
for (indexX = 0;indexX < 9 ; indexX++)
{
KIntVarArray tmpY;
for (indexY = 0;indexY < 9 ; indexY++)
{
tmpY += *vars[indexX][indexY];
}
problem.post(new KAllDifferent("alldiffVert",tmpY,KAllDifferent::GENERALIZED_ARC_CONSISTENCY));
}
// All-different values in columns
for (indexY = 0;indexY < 9 ; indexY++)
{
KIntVarArray tmpX;
for (indexX = 0;indexX < 9 ; indexX++)
{
tmpX += *vars[indexX][indexY];
}
problem.post(new KAllDifferent("alldiffHoriz",tmpX,KAllDifferent::GENERALIZED_ARC_CONSISTENCY));
}
// All-different values in 3x3 squares
int i,j;
for (j=0;j<3;j++)
{
for (i=0;i<3;i++)
{
KIntVarArray tmpXY;
for (indexY = i*3;indexY < i*3+3 ; indexY++)
{
for (indexX = j*3;indexX < j*3+3 ; indexX++)
{
tmpXY += *vars[indexX][indexY];
}
}
problem.post(new KAllDifferent("alldiff3x3",tmpXY,KAllDifferent::GENERALIZED_ARC_CONSISTENCY));
}
}
// propagating problem
if (problem.propagate())
{
printf("Problem is infeasible\n");
exit(1);
}
// creation of the solver
KSolver solver(problem);
// look for all solutions
int result = solver.findAllSolutions();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();
printf("|-------|-------|-------|\n");
for (indexY = 0;indexY < 9 ; indexY++)
{
printf("| %i %i %i | %i %i %i | %i %i %i |\n",
sol->getValue(*vars[0][indexY]),
sol->getValue(*vars[1][indexY]),
sol->getValue(*vars[2][indexY]),
sol->getValue(*vars[3][indexY]),
sol->getValue(*vars[4][indexY]),
sol->getValue(*vars[5][indexY]),
sol->getValue(*vars[6][indexY]),
sol->getValue(*vars[7][indexY]),
sol->getValue(*vars[8][indexY])
);
if (indexY % 3 == 2)
{
printf("|-------|-------|-------|\n");
}
}
// memory desallocation
for (indexX = 0;indexX < 9 ; indexX++)
{
for (indexY = 0;indexY < 9 ; indexY++)
{
delete vars[indexX][indexY];
}
delete[] vars[indexX];
}
delete[] vars;
import sys, os
from kalis import *
# Creation of the session
session = KSession()
# Creation of the problem in this session
problem = KProblem(session, "Sudoku")
# Creation of a 9x9 matrix of KintVar
vars = [
[
KIntVar(problem, "v[{},{}]".format(i,j), 1, 9)
for j in xrange(9)
]
for i in xrange(9)
]
pb = raw_input("Enter problem to be solved (1 or 2): ")
# Data from "The Guardian", 29 July, 2005. http://www.guardian.co.uk/sudoku
if pb == "1":
vars[0][0].instantiate(8); vars[5][0].instantiate(3)
vars[1][1].instantiate(5); vars[6][1].instantiate(4)
vars[0][2].instantiate(2); vars[4][2].instantiate(7); vars[7][2].instantiate(6)
vars[3][3].instantiate(1); vars[8][3].instantiate(5)
vars[2][4].instantiate(3); vars[6][4].instantiate(9)
vars[0][5].instantiate(6); vars[5][5].instantiate(4)
vars[1][6].instantiate(7); vars[4][6].instantiate(2); vars[8][6].instantiate(3)
vars[2][7].instantiate(4); vars[7][7].instantiate(1)
vars[3][8].instantiate(9); vars[8][8].instantiate(8)
elif pb == "2":
vars[0][3].instantiate(3); vars[0][6].instantiate(5)
vars[1][4].instantiate(4); vars[1][7].instantiate(8)
vars[2][1].instantiate(1); vars[2][3].instantiate(5)
vars[2][4].instantiate(7); vars[2][5].instantiate(9)
vars[2][6].instantiate(4); vars[2][8].instantiate(3)
vars[3][0].instantiate(5); vars[3][2].instantiate(2)
vars[4][2].instantiate(4); vars[4][6].instantiate(1)
vars[5][6].instantiate(9); vars[5][8].instantiate(7)
vars[6][0].instantiate(4); vars[6][2].instantiate(7)
vars[6][3].instantiate(9); vars[6][4].instantiate(1)
vars[6][5].instantiate(5); vars[6][7].instantiate(3)
vars[7][1].instantiate(6); vars[7][4].instantiate(8)
vars[8][2].instantiate(1); vars[8][5].instantiate(3)
else:
print "problem must be 1 or 2, not {}".format(pb)
del session
exit(1)
# All-different values in rows
for i in xrange(9):
tmpI = KIntVarArray()
for j in xrange(9):
tmpI.add(vars[i][j])
problem.post(KAllDifferent("alldiffVert {}".format(i), tmpI, KAllDifferent.GENERALIZED_ARC_CONSISTENCY))
# All-different values in columns
for j in xrange(9):
tmpJ = KIntVarArray()
for i in xrange(9):
tmpJ.add(vars[i][j])
problem.post(KAllDifferent("alldiffHoriz {}".format(j), tmpJ, KAllDifferent.GENERALIZED_ARC_CONSISTENCY))
# All-different values in 3x3 squares
for offsetI in xrange(0,9,3):
for offsetJ in xrange(0,9,3):
tmpIJ = KIntVarArray()
for i in xrange(3):
for j in xrange(3):
tmpIJ.add(vars[i + offsetI][j + offsetJ])
problem.post(KAllDifferent("alldiff3x3 {},{}".format(offsetI, offsetJ), tmpIJ, KAllDifferent.GENERALIZED_ARC_CONSISTENCY))
# Propagate problem
if problem.propagate():
print "Problem is infeasible"
exit(1)
# Solve the problem
solver = KSolver(problem)
solver.findAllSolutions()
# Get solution
sol = problem.getSolution()
# Print solution resume
sol.printResume();
print "|-------|-------|-------|"
for j in xrange(9):
print "| {} {} {} | {} {} {} | {} {} {} |".format(
sol.getValue(vars[0][j]), sol.getValue(vars[1][j]), sol.getValue(vars[2][j]),
sol.getValue(vars[3][j]), sol.getValue(vars[4][j]), sol.getValue(vars[5][j]),
sol.getValue(vars[6][j]), sol.getValue(vars[7][j]), sol.getValue(vars[8][j])
)
if j % 3 == 2:
print "|-------|-------|-------|"
del session
import com.artelys.kalis.*;
import java.io.*;
public class Sudoku {
public static void main(String[] args) {
try {
System.loadLibrary("Kalis"); // uses java option -Djava.library.path=path to find Kalis.dll
System.loadLibrary("KalisJava"); // uses java option -Djava.library.path=path to find KalisJava.dll
KSession session = new KSession();
// Creation of the problem in this session
KProblem problem = new KProblem(session, "Sudoku", 4);
KIntVar[][] vars = new KIntVar[9][9];
int i, j;
for (i = 0; i < 9; i++) {
for (j = 0; j < 9; j++) {
vars[i][j] = new KIntVar(problem, String.format("v[%d,%d]",
i, j), 1, 9);
}
}
System.out.print("Enter problem to be solved (1 or 2): ");
BufferedReader br = new BufferedReader(new InputStreamReader(
System.in));
String pb = br.readLine();
if (pb.equals("1")) {
vars[0][0].instantiate(8);
vars[5][0].instantiate(3);
vars[1][1].instantiate(5);
vars[6][1].instantiate(4);
vars[0][2].instantiate(2);
vars[4][2].instantiate(7);
vars[7][2].instantiate(6);
vars[3][3].instantiate(1);
vars[8][3].instantiate(5);
vars[2][4].instantiate(3);
vars[6][4].instantiate(9);
vars[0][5].instantiate(6);
vars[5][5].instantiate(4);
vars[1][6].instantiate(7);
vars[4][6].instantiate(2);
vars[8][6].instantiate(3);
vars[2][7].instantiate(4);
vars[7][7].instantiate(1);
vars[3][8].instantiate(9);
vars[8][8].instantiate(8);
} else if (pb.equals("2")) {
vars[0][3].instantiate(3);
vars[0][6].instantiate(5);
vars[1][4].instantiate(4);
vars[1][7].instantiate(8);
vars[2][1].instantiate(1);
vars[2][3].instantiate(5);
vars[2][4].instantiate(7);
vars[2][5].instantiate(9);
vars[2][6].instantiate(4);
vars[2][8].instantiate(3);
vars[3][0].instantiate(5);
vars[3][2].instantiate(2);
vars[4][2].instantiate(4);
vars[4][6].instantiate(1);
vars[5][6].instantiate(9);
vars[5][8].instantiate(7);
vars[6][0].instantiate(4);
vars[6][2].instantiate(7);
vars[6][3].instantiate(9);
vars[6][4].instantiate(1);
vars[6][5].instantiate(5);
vars[6][7].instantiate(3);
vars[7][1].instantiate(6);
vars[7][4].instantiate(8);
vars[8][2].instantiate(1);
vars[8][5].instantiate(3);
} else {
throw new RuntimeException(String.format(
"problem must be 1 or 2, not '%s'", pb));
}
// *** Modeling of the problem
i = 0;
for (KIntVar[] row : vars) {
KIntVarArray tmpRow = new KIntVarArray();
for (KIntVar cell : row) {
tmpRow.add(cell);
}
problem.post(new KAllDifferent(
String.format("alldiffHoriz#%d", i++),
tmpRow,
KAllDifferent.PropagationLevel.GENERALIZED_ARC_CONSISTENCY
.swigValue()));
}
for(i = 0; i < 9; i++) {
KIntVarArray tmpCol = new KIntVarArray();
for(j = 0; j < 9; j++) {
tmpCol.add(vars[j][i]);
}
problem.post(new KAllDifferent(
String.format("alldiffVert#%d", i),
tmpCol,
KAllDifferent.PropagationLevel.GENERALIZED_ARC_CONSISTENCY
.swigValue()));
}
int[] offsets = {0,3,6};
for(int offsetI : offsets) {
for(int offsetJ : offsets) {
KIntVarArray tmpSquare = new KIntVarArray();
for(i = offsetI; i < offsetI+3; i++) {
for(j = offsetJ; j < offsetJ+3; j++) {
tmpSquare.add(vars[j][i]);
}
}
problem.post(new KAllDifferent(
String.format("alldiff%dx%d", offsetI, offsetJ),
tmpSquare,
KAllDifferent.PropagationLevel.GENERALIZED_ARC_CONSISTENCY
.swigValue()));
}
}
if (problem.propagate()) {
throw new RuntimeException("Problem is infeasible");
}
KSolver solver = new KSolver(problem);
solver.findAllSolutions();
KSolution sol = problem.getSolution();
sol.printResume();
System.out.println("|-------|-------|-------|");
for(j = 0; j < 9; j++) {
System.out.println(String.format("| %d %d %d | %d %d %d | %d %d %d |",
sol.getValue(vars[0][j]), sol.getValue(vars[1][j]), sol.getValue(vars[2][j]),
sol.getValue(vars[3][j]), sol.getValue(vars[4][j]), sol.getValue(vars[5][j]),
sol.getValue(vars[6][j]), sol.getValue(vars[7][j]), sol.getValue(vars[8][j])));
if (j % 3 == 2)
System.out.println("|-------|-------|-------|");
}
} catch (Exception e) {
e.printStackTrace();
}
}
}
