Improvement techniques¶
In this chapter, you will get to know two improvement techniques often used in modeling problems using constraint programming:
symmetry removal ;
redundant constraints.
Symmetry removal¶
For many optimization problems, some variables are equivalent and interchangeable. It may occur when you want to sell products with equivalent characteristics considering your constraints and producing the same revenue. Another example happens when you want to assign a job to a group of people having the same skills. When using the standard model, Artelys Kalis can provide many equivalent solutions just by changing the role of two such variables. This can be avoided by introducing a relation of order.
A simple example can be made using the knapsack problem defined in Chapter 8. Two projects are strictly equivalent: the 4th and 6th. Both have a revenue of 400 and a cost of 80. If only one of theme remains in the optimal solution, we can enforce that it is the 4th one. It means that the associated binary variable associated to projectchosen[3] must be greater or equal to projectChosen[5].
A more general code would be:
for(int i = 0; i < nbProj; i++) {
for(int j = i+1; j < nbProj; j++) {
if ((projValues[i] == projValues[j]) && (constrCoeffs[0][i] == constrCoeffs[0][j])) {
knapsack.post( projectChosen[i] >= projectChosen[j]);
}
}
}
for i in range(nbProj):
for j in range(i+1, nbProj):
if projValues[i] == projValues[j] and constrCoeffs[0][i] == constrCoeffs[0][j]:
knapsack.post(projectChosen[i] >= projectChosen[j])
for(int i = 0; i < nbProj; i++)
{
for(int j = i+1; j < nbProj; j++)
{
if ((projValues[i] == projValues[j]) && (constrCoeffs[0][i] == constrCoeffs[0][j]))
{
knapsack.post(new KGreaterOrEqualXyc(projectChosen.getElt(i), projectChosen.getElt(j),0));
}
}
}
Considering this example and different strategies already used, the number of visited nodes was reduced between 3 and 25 %.
In case of multiple variables equivalence, many more cases will be removed by adding a global order.
For example, we can consider three projects having the same characteristics. The possible values for there associated variables 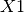 ,
, 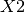 and
and 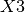 would be reduced from:
would be reduced from:
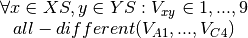
by adding the constraint: 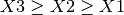 .
.
This will help the search to reduce drastically the number of explored nodes without changing the optimum.
Redundant constraints¶
Adding redundant constraints to a model is the main improvement method used in constraint programming. A redundant constraint occurs when it is implied by other constraints of the problem. In fact, it gives just a different representation of a part of these constraints. The interest of redundant constraints is a better propagation. In fact, due to incomplete propagation, this avoid infeasible assignments earlier in the tree search.
Here is a simple example showing this amelioration.
Consider the following problem:
![\text{Variables:} &\\
&X, Y \in [0,10] \\
&X, Y \text{are integers} \\
\\
\text{Constraints:} &\\
&C1: 2X + 3Y \geq 11 \\
&C2: X - 3Y \geq 4](_images/math/4af33769b88c39025160352fc9b3b84beb0dab17.png)
Usual propagation on linear constraints is made on lower and upper bounds of each variable.
In that case we can propagate 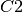 and we will obtain:
and we will obtain: ![X \in [4,10]](_images/math/b9822609446f48a6a50f0e7877f6e3530bb865a7.png) and
and ![Y \in [0,2]](_images/math/cb27c645ab5ec49dbc8b337633f83ae2fda635d9.png) . No more propagation can be done.
. No more propagation can be done.
Now we add a redundant constraint 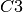 with is just a linear combination of the others:
with is just a linear combination of the others: 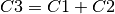 . Thus
. Thus 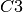 is
is 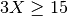 .
.
Considering this redundant constraint, we can complete the initial propagation with 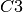 and deduce a new domain for
and deduce a new domain for 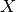 .
.
It gives: ![X \in [5,10]](_images/math/e29c1f610d6f92331816894ad4e7291d6e3ec5a7.png) and
and ![Y \in [0,2]](_images/math/cb27c645ab5ec49dbc8b337633f83ae2fda635d9.png) .
.
This small example shows the interest of redundant constraints. Their application in real problems will often be made with global constraints which include powerful, but incomplete, propagation.
Do not abuse of them, they consume memory and may increase time computation in some cases.