Euler knight tour¶
Our task is to find a tour on a chessboard for a knight figure such that the knight moves through every cell exactly once and at the end of the tour returns to its starting point. The path of the knight must follow the standard chess rules: a knight moves either one cell vertically and two cells horizontally, or two cells in the vertical and one cell in the horizontal direction, as shown in the following graphic (Fig. 27):
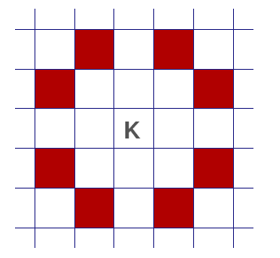
Fig. 27 Permissible moves for a knight¶
Model formulation¶
To represent the chessboard we number the cells from  to
to 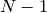 , where
, where 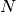 is the number of cells of the board. The path of the knight is defined by
is the number of cells of the board. The path of the knight is defined by 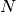 variables
variables 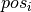 that indicate the ith position of the knight on its tour. The first variable is fixed to zero as the start of the tour. Another obvious constraint we need to state is that all variables
that indicate the ith position of the knight on its tour. The first variable is fixed to zero as the start of the tour. Another obvious constraint we need to state is that all variables 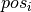 take different values (every cell of the chessboard is visited exactly once):
take different values (every cell of the chessboard is visited exactly once):
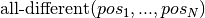
We are now left with the necessity to establish a constraint relation that checks whether consecutive positions define a valid knight move. To this aim we define a new binary constraint valid_knight_move that checks whether a given pair of values defines a permissible move according to the chess rules for knight moves. Vertically and horizontally, the two values must be no more than two cells apart and the sum of the vertical and horizontal difference must be equal to three. The complete model then looks as follows.
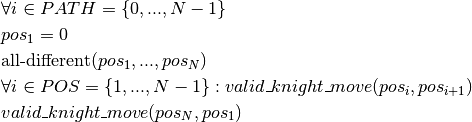
Implementation¶
Testing whether moving from position a to position b is a valid move for a knight figure can be done with the following function KnightMoveOk() :
bool KnightMoveOk(int a,int b,int S) {
int xa,ya,xb,yb,delta_x,delta_y;
xa = a / S;
ya = a % S;
xb = b / S;
yb = b % S;
delta_x = abs(xa-xb);
delta_y = abs(ya-yb);
return (delta_x<=2) && (delta_y<=2) && (delta_x+delta_y==3);
}
def KnightMoveOk(a: int, b: int, nb_rows: int) -> bool:
xa = a // nb_rows
ya = a % nb_rows
xb = b // nb_rows
yb = b % nb_rows
delta_x = abs(xa - xb)
delta_y = abs(ya - yb)
return (delta_x <= 2) and (delta_y <= 2) and (delta_x + delta_y <= 3)
public boolean KnightMoveOk(int a,int b, int S) {
int xa = a / S;
int ya = a % S;
int xb = b / S;
int yb = b % S;
int delta_x = (xa>xb)? xa-xb : xb - xa;
int delta_y = (ya>yb)? ya-yb : yb - ya;
return delta_x<=2 && delta_y<=2 && delta_x+delta_y==3;
}
The following model defines the user constraint function valid KnightMoveOk as the implementation of the new binary constraints on pairs of 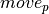 variables (the constraints are established with
variables (the constraints are established with KACBinTableConstraint).
// Number of rows/columns
int S = 8;
// Total number of cells
int N = S * S;
// Cell at position p in the tour
KIntVarArray pos;
// Creation of the problem in this session
KProblem problem(session,"Euler Knight");
// variables creation
char name[80];
int j,i;
for (j=0;j<N;j++) {
sprintf(name,"pos(%i)",j);
pos += (* new KIntVar( problem,name,0,N-1) );
}
// Fix the start position
pos[0].instantiate(0);
// Each cell is visited once
problem.post(new KAllDifferent("alldiff",pos,KAllDifferent::GENERALIZED_ARC_CONSISTENCY));
// The path of the knight obeys the chess rules for valid knight moves
bool ** tab;
tab = new bool*[N];
int v1,v2;
for (v1=0;v1<N;v1++) {
tab[v1] = new bool[N];
}
for (v1=0;v1<N;v1++) {
for (v2=0;v2<N;v2++) {
tab[v1][v2] = KnightMoveOk(v1,v2,S);
}
}
for (i=0;i<N-1;i++) { problem.post(KACBinTableConstraint(pos[i],pos[i+1],tab,KACBinTableConstraint::ALGORITHM_AC2001,"KnightMove"));
}
// the Knight must return to its first position
problem.post(KACBinTableConstraint(pos[N-1],pos[0],tab,KACBinTableConstraint::ALGORITHM_AC2001,"KnightMove"));
// Setting enumeration parameters
KBranchingSchemeArray myBa;
myBa += KProbe(KSmallestMin(),KMaxToMin(),pos,14);
// Solve the problem
// creation of the solver
KSolver solver(problem,myBa);
// propagating problem
if (problem.propagate()) {
printf("Problem is infeasible\n");
exit(1);
}
int result = solver.solve();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();
for (j=0;j<N;j++) {
printf("%i -> ",sol->getValue(pos[j]));
}
printf("0\n");
from kalis import *
### Data
# Number of rows/columns
nb_rows = 8
# Total number of cells
N = nb_rows * nb_rows
### Variables creation
# Creation of the Kalis session and of the optimization problem
session = KSession()
problem = KProblem(session, "Euler Knight")
# Cell at position p in the tour
positions = KIntVarArray()
for p in range(N):
positions += KIntVar(problem, "pos(%d)" % p, 0, N-1)
### Constraints creation
# Fix the start position
positions[0].instantiate(0)
# Each cell is visited once
problem.post(KAllDifferent("alldiff", positions, KAllDifferent.GENERALIZED_ARC_CONSISTENCY))
# The path of the knight obeys the chess rules for valid knight moves
allowed_moves_table = [[KnightMoveOk(v1, v2, nb_rows) for v2 in range(N)] for v1 in range(N)]
for i in range(N - 1):
problem.post(KACBinTableConstraint(positions[i], positions[i + 1],
allowed_moves_table,
KACBinTableConstraint.ALGORITHM_AC2001,
"KnightMove"))
# The Knight must return to its first position
problem.post(KACBinTableConstraint(positions[N - 1], positions[0],
allowed_moves_table,
KACBinTableConstraint.ALGORITHM_AC2001,
"KnightMove"))
### Solve the problem
# First propagation to check inconsistency
if problem.propagate():
print("Problem is infeasible")
sys.exit(1)
# Setting enumeration parameters
my_branching_array = KBranchingSchemeArray()
my_branching_array += KProbe(KSmallestMin(), KMaxToMin(), positions, 14)
# Set the solver
solver = KSolver(problem, my_branching_array)
# Run optimization
result = solver.solve()
# Solution printing
if result:
solution = problem.getSolution()
solution.printResume()
for i in range(N):
print(solution.getValue(positions[i]), end=" ")
print("0")
//todo
The branching scheme used in this model is the KProbe heuristic, in combination with the variable selection KSmallestMin (choose variable with smallest lower bound) and the value selection criterion KMaxToMin (from largest to smallest domain value). Our model defines one parameter. It is thus possible to change the size of the chessboard (S) when executing the model without having to modify the model source.
Alternative implementation¶
Whereas the aim of the model above is to give an example of the definition of user constraints, it is possible to implement this problem in a more efficient way using the model developed for the previous cyclic scheduling problem. The set of successors (domains of variables 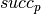 ) can be calculated using the same algorithm that we have used above in the implementation of the user-defined binary constraints. Without repeating the complete model definition at this place, we simply display the model formulation, including the calculation of the sets of possible successors (procedure calculate_successors, and the modified procedure print_sol for solution printout). We use a simpler version of the cycle constraints than the one we have seen in previous section, its only argument is the set of successor variables as there are no weights to the arcs in this problem.
) can be calculated using the same algorithm that we have used above in the implementation of the user-defined binary constraints. Without repeating the complete model definition at this place, we simply display the model formulation, including the calculation of the sets of possible successors (procedure calculate_successors, and the modified procedure print_sol for solution printout). We use a simpler version of the cycle constraints than the one we have seen in previous section, its only argument is the set of successor variables as there are no weights to the arcs in this problem.
// Total number of cells
int N = S * S;
// Cell at position p in the tour
KIntVarArray succ;
// Creation of the problem in this session
KProblem problem(session,"Euler Knight 2");
// variables creation
char name[80];
int j,i;
for (j=0;j<N;j++) {
sprintf(name,"succ(%i)",j);
succ += (* new KIntVar( problem,name,0,N-1) );
}
// Calculate set of possible successors
for (j=0;j<N;j++) {
for (i=0;i<N;i++) {
if (!KnightMoveOk(j,i,S)) {
// i is not a possible successor for j
succ[j].remVal(i);
}
}
}
// Each cell is visited once, no subtours
problem.post(new KCycle(&succ,NULL,NULL,NULL));
// Solve the problem
// creation of the solver
KSolver solver(problem);
// propagating problem
if (problem.propagate()) {
printf("Problem is infeasible\n");
exit(1);
}
int result = solver.solve();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();
int thispos=0;
int nextpos=sol->getValue(succ[0]);
while (nextpos!=0) {
printf("%i -> ",thispos);
thispos=nextpos;
nextpos=sol->getValue(succ[thispos]);
}
printf("0\n");
#todo
// Number of rows/columns
int S = 8;
// Total number of cells
int N = S * S;
// Cell at position p in the tour
KIntVarArray succ = new KIntVarArray();
// variables creation
int j, i;
for (j = 0; j < N; j++)
{
succ.add(new KIntVar(problem, "succ(" + j + ")", 0, N - 1));
}
// Calculate set of possible successors
for (j = 0; j < N; j++)
{
for (i = 0; i < N; i++)
{
if (!KnightMoveOk(j, i, S))
{
// i is not a possible successor for j
succ.getElt(j).remVal(i);
}
}
}
// Each cell is visited once, no subtours
problem.post(new KCycle(succ, null, null, null));
// Solve the problem
// creation of the solver
KSolver solver = new KSolver(problem);
// propagating problem
if (problem.propagate())
{
System.out.println("Problem is infeasible");
exit(1);
}
int result = solver.solve();
// solution printing
KSolution sol = problem.getSolution();
// print solution resume
sol.printResume();
int thispos = 0;
int nextpos = sol.getValue(succ.getElt(0));
while (nextpos != 0)
{
System.out.print(thispos + " -> ");
thispos = nextpos;
nextpos = sol.getValue(succ.getElt(thispos));
}
System.out.println("0\n");
The calculation of the domains for the 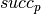 variables reduces these to 2-8 elements (as compared to the
variables reduces these to 2-8 elements (as compared to the 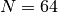 values for every
values for every 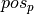 variables), which clearly reduces the search space for this problem. This second model finds the first solution to the problem after 131 nodes taking just a fraction of a second to execute on a standard PC whereas the first model requires several thousand nodes and considerably longer running times. It is possible to reduce the number of branch-and-bound nodes even further by using yet another version of the cycle constraint that works with successor and predecessor variables. This version of cycle performs a larger amount of propagation, at the expense of (slightly) slower execution times for our problem when S < 8. For S > 8, the computation expense due to the stronger propagation pays. This compromise strength of propagation / nodes explored is typical of hard combinatorial problems where the need of stronger propagation arise for a certain size of the problem. Below this size, a simpler but faster propagation is the best choice. Above this size, the stronger propagation scheme gives the best results and is sometime necessary to find solution in a reasonnable time. As the limit of size for this behavior is problem dependent, the user is therefore encouraged to try both algorithms.
variables), which clearly reduces the search space for this problem. This second model finds the first solution to the problem after 131 nodes taking just a fraction of a second to execute on a standard PC whereas the first model requires several thousand nodes and considerably longer running times. It is possible to reduce the number of branch-and-bound nodes even further by using yet another version of the cycle constraint that works with successor and predecessor variables. This version of cycle performs a larger amount of propagation, at the expense of (slightly) slower execution times for our problem when S < 8. For S > 8, the computation expense due to the stronger propagation pays. This compromise strength of propagation / nodes explored is typical of hard combinatorial problems where the need of stronger propagation arise for a certain size of the problem. Below this size, a simpler but faster propagation is the best choice. Above this size, the stronger propagation scheme gives the best results and is sometime necessary to find solution in a reasonnable time. As the limit of size for this behavior is problem dependent, the user is therefore encouraged to try both algorithms.

Fig. 28 Graphical representation of a knight’s tour with on a 24x24 chessboard¶
