Assignment with allowed groups¶

Problem description¶

Let us consider now an assignment problem in which only certain allowed groups of workers can be assigned to the tasks. Let derive directly an example here.

Consider there are twelve workers, numbered $0$ - $11$ . The allowed groups are combinations of the following pairs of workers.

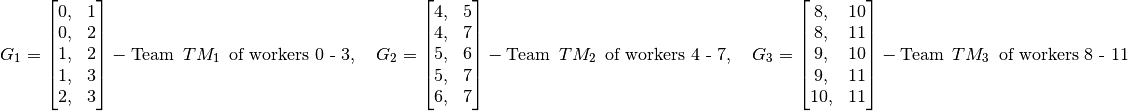
$G_1 = \begin{bmatrix} 0, & 1 \\ 0, & 2 \\ 1, & 2 \\ 1, & 3 \\ 2, & 3 \\ \end{bmatrix} - \text{Team} \hspace{0.5em} TM_1 \hspace{0.5em} \text{of workers 0 - 3}, \quad G_2 = \begin{bmatrix} 4, & 5 \\ 4, & 7 \\ 5, & 6 \\ 5, & 7 \\ 6, & 7 \\ \end{bmatrix} - \text{Team} \hspace{0.5em} TM_2 \hspace{0.5em} \text{of workers 4 - 7}, \quad G_3 = \begin{bmatrix} 8, & 10 \\ 8, & 11 \\ 9, & 10 \\ 9, & 11 \\ 10, & 11 \\ \end{bmatrix} - \text{Team} \hspace{0.5em} TM_3 \hspace{0.5em} \text{of workers 8 - 11}$

An allowed group can be any combination of three pairs of workers, one pair from each of 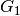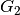$G_1$ , $G_2$ , and $G_3$ .

For example, combining [2, 3], [6, 7], and [10, 11] results in the allowed group [2, 3, 6, 7, 10, 11].

Since each of the three sets contains five elements, the total number of allowed groups is 5 * 5 * 5 = 125.

To model this constraint, we would like to introduce a constraint GAC (Generalized Arc Consistency) in a table version. It means that we would like to define all combinations within a table, and add a constraint over the variables to be part of one of the combination.

More precisely, for the team 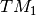$TM_1$ we will introduce variables 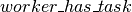$worker\_has\_task$ to be able to know if a task is perform by the worker. Then, 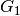$G_1$ constraint can be expressed :

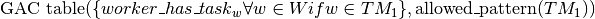
$\text{GAC table}(\{worker\_has\_task_w \forall w \in W if w \in TM_1 \}, \text{allowed\_pattern}(TM_1))$

with

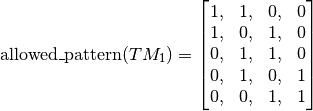
$\text{allowed\_pattern}(TM_1) = \begin{bmatrix} 1, & 1, & 0, & 0 \\ 1, & 0, & 1, & 0 \\ 0, & 1, & 1, & 0 \\ 0, & 1, & 0, & 1 \\ 0, & 0, & 1, & 1 \\ \end{bmatrix}$

Implementation with a GAC constraint¶

This is a non-convex problem and the constraint ‘only some pair of workers are allowed to work together’ can be difficult to implement. In the first version, the Kalis class KGeneralizedArcConsistencyConstraint is used to create a ValidTeamPattern class by overloading the testIfSatisfied method to make it check wether the worker assigned to some tasks are actually allowed.

This implementation can be done as follows:

class ValidTeamPattern(KGeneralizedArcConsistencyConstraint):
    """This class ineherits from the KACBinConstraint and allow to define a custom binary
    arc-consistency constraint."""

    def __init__(self, vars, valid_combination):
        """Initialize the StartingTimeCombinationGAC constraint."""
        KGeneralizedArcConsistencyConstraint.__init__(self, vars,
                                                      KGeneralizedArcConsistencyConstraint.GENERALIZED_ARC_CONSISTENCY,
                                                      "StartingTimeCombinationGAC")
        self.vars = vars
        self.valid_combination = valid_combination

    def testIfSatisfied(self, values):
        """Overload the 'testIfSatisfied' method in 'KGeneralizedArcConsistencyConstraint' class by using a user
        defined function. """
        return list(values) in self.valid_combination


def allowed_pattern(allowed_groups_team: list, teams_worker: list) -> list:
    """ Creation of an array summing up the allowed groups from a team. The output has the following format :
        [[0, 1, 0, 1],
         [1, 0, 0, 1]]

         In this example, the first line allows the second and fourth workers to work together and the second line
         allows the first and fourth workers to work together.
    """

    res = []
    for group in allowed_groups_team:
        combination = []
        for worker in teams_worker:
            combination += [1] if worker in group else [0]
        res += [combination]
    return res


def solve(cost_matrix: list, allowed_groups: list):
    # Get the number of tasks and workers from the cost matrix
    nb_worker = len(cost_matrix)
    nb_task = len(cost_matrix[1])

    # Get the number of groups from the allowed_groups array
    nb_teams = len(allowed_groups)

    # Get the composition of the teams from the allowed_groups array
    teams_worker = []
    for team in range(nb_teams):
        teams_worker += [[]]
        for pair in allowed_groups[team]:
            for worker in pair:
                if worker not in teams_worker[team]:
                    teams_worker[team] += [worker]

    try:
        # Declaration of the problem
        session = KSession()
        problem = KProblem(session, "allowed_groups")

        # Variable declaration
        # Declaration of a binary variable for each task/worker combination, stating whether the task has been assigned
        # to the worker
        worker_has_task = {}
        for worker in range(nb_worker):
            worker_has_task[worker] = KIntVarArray()
            for task in range(nb_task):
                worker_has_task[worker] += KIntVar(problem, "Worker_{}_Task_{}".format(worker, task), 0, 1)

        # Constraint declaration
        # Ensure that each task is assigned once
        for task in range(nb_task):
            problem.post(sum(worker_has_task[worker][task] for worker in range(nb_worker)) == 1)

        # Ensure that the selected workers from each team are allowed to work together
        # First a variable counting the number of tasks allocated to each worker is created. Those variables are binary,
        # thus ensuring that every worker has one tasks at most
        nb_task_worker = KIntVarArray()
        for worker in range(nb_worker):
            nb_task_worker += KIntVar(problem, "Nb_task_worker_{}".format(worker), 0, 1)
            problem.post(nb_task_worker[worker] == sum(worker_has_task[worker][task] for task in range(nb_task)))

        # Post the allowed group constraint
        patterns = {}
        allowed = {}
        for team in range(nb_teams):
            patterns[team] = KIntVarArray()
            for worker in teams_worker[team]:
                patterns[team] += nb_task_worker[worker]
            allowed_pattern_array = allowed_pattern(allowed_groups[team], teams_worker[team])
            allowed[team] = ValidTeamPattern(patterns[team], allowed_pattern_array)
            problem.post(allowed[team])

        # Objective declaration
        # The objective will be greater than nb_task * the minimum of cost_matrix and lower than the sum of the
        # coefficients in cost_matrix
        objective_sup = sum(cost_matrix[worker][task] for task in range(nb_task) for worker in range(nb_worker))
        objective_inf = nb_task * min(
            cost_matrix[worker][task] for task in range(nb_task) for worker in range(nb_worker))

        # The objective is the sum of the costs
        objective = KIntVar(problem, "cost", objective_inf, objective_sup)
        problem.post(objective == sum(cost_matrix[worker][task] * worker_has_task[worker][task] for task in
                                      range(nb_task) for worker in range(nb_worker)))

        # Set the objective
        problem.setSense(KProblem.Minimize)
        problem.setObjective(objective)

        # Set the solver
        solver = KSolver(problem)

        # If the problem is infeasible
        if problem.propagate():
            # Display of various details to help find the source of the problem
            problem.display()
            problem.printMinimalConflictSet()
            print("Problem is infeasible")
            exit()

        # Launch the optimization
        result = solver.optimize()

        if result:
            solution = problem.getSolution()
            # Display the solution
            for task in range(nb_task):
                for worker in range(nb_worker):
                    if solution.getValue(worker_has_task[worker][task]) == 1:
                        print(
                            f'Task {task} has been affected to worker {worker} 'f'with cost {cost_matrix[worker][task]}')
            print(f'Total cost : {solution.getValue(objective)}')

            # Return the objective
            problem.getSolution().display()
            return solution.getValue(objective)


    except ArtelysException as e:
        print(e)


if __name__ == '__main__':
    COST = [[90, 76, 75, 70, 50, 74],
            [35, 85, 55, 65, 48, 101],
            [125, 95, 90, 105, 59, 120],
            [45, 110, 95, 115, 104, 83],
            [60, 105, 80, 75, 59, 62],
            [45, 65, 110, 95, 47, 31],
            [38, 51, 107, 41, 69, 99],
            [47, 85, 57, 71, 92, 77],
            [39, 63, 97, 49, 118, 56],
            [47, 101, 71, 60, 88, 109],
            [17, 39, 103, 64, 61, 92],
            [101, 45, 83, 59, 92, 27]]

    ALLOWED_GROUPS = [[[2, 3], [1, 3], [1, 2], [0, 1], [0, 2]],
                      [[6, 7], [5, 7], [5, 6], [4, 5], [4, 7]],
                      [[10, 11], [9, 11], [9, 10], [8, 10], [8, 11]]]

    solve(COST, ALLOWED_GROUPS)

Implementation with a GAC table constraint¶

The GAC method implemented above shows how any constraint can be implemented simply by overloading the testIfSatisfied method. However, the KGeneralizedArcConsistencyTableConstraint class already implemented in Kalis is precisely made to ensure that the value taken by a set of variable is equal to one of the sets of variables present in a tuple.

A way to implement this method is as follows :

def allowed_pattern(allowed_groups_team: list, teams_worker: list) -> KTupleArray:
    """ Creation of an array summing up the allowed groups from a team. The output has the following format :
        [[0, 1, 0, 1],
         [1, 0, 0, 1]]

         In this example, the first line allows the second and fourth workers to work together and the second line
         allows the first and fourth workers to work together.
    """
    res = KTupleArray()
    for group in allowed_groups_team:
        combination = KIntArray()
        for worker in teams_worker:
            combination += 1 if worker in group else 0
        res += combination
    res.display()
    return res


def solve(cost_matrix: list, allowed_groups: list):
    # Get the number of tasks and workers from the cost matrix
    nb_worker = len(cost_matrix)
    nb_task = len(cost_matrix[1])

    # Get the number of groups from the allowed_groups array
    nb_teams = len(allowed_groups)

    # Get the composition of the teams from the allowed_groups array
    teams_worker = []
    for team in range(nb_teams):
        teams_worker += [[]]
        for pair in allowed_groups[team]:
            for worker in pair:
                if worker not in teams_worker[team]:
                    teams_worker[team] += [worker]

    try:
        # Declaration of the problem
        session = KSession()
        problem = KProblem(session, "allowed_groups")

        # Variable declaration
        # Declaration of a binary variable for each task/worker combination, stating wether the task has been assigned
        # to the worker
        worker_has_task = {}
        for worker in range(nb_worker):
            worker_has_task[worker] = KIntVarArray()
            for task in range(nb_task):
                worker_has_task[worker] += KIntVar(problem, "Worker_{}_Task_{}".format(worker, task), 0, 1)

        # Constraint declaration
        # Ensure that each task is assigned once
        for task in range(nb_task):
            problem.post(sum(worker_has_task[worker][task] for worker in range(nb_worker)) == 1)

        # Ensure that the selected workers from each team are allowed to work together
        # First a variable counting the number of tasks allocated to each worker is created. Those variables are binary,
        # thus ensuring that every worker has one tasks at most
        nb_task_worker = KIntVarArray()
        for worker in range(nb_worker):
            nb_task_worker += KIntVar(problem, "Nb_task_worker_{}".format(worker), 0, 1)
            problem.post(nb_task_worker[worker] == sum(worker_has_task[worker][task] for task in range(nb_task)))

        # Post the allowed group constraint
        patterns = {}
        allowed = {}
        for team in range(nb_teams):
            patterns[team] = KIntVarArray()
            for worker in teams_worker[team]:
                patterns[team] += nb_task_worker[worker]
            allowed_pattern_array = allowed_pattern(allowed_groups[team], teams_worker[team])
            allowed[team] = KGeneralizedArcConsistencyTableConstraint(patterns[team], allowed_pattern_array,
                                                                      "Pair_team_{}".format(team))
            problem.post(allowed[team])

        # Objective declaration
        # The objective will be greater than nb_task * the minimum of cost_matrix and lower than the sum of the
        # coefficients in cost_matrix
        objective_sup = sum(cost_matrix[worker][task] for task in range(nb_task) for worker in range(nb_worker))
        objective_inf = nb_task * min(
            cost_matrix[worker][task] for task in range(nb_task) for worker in range(nb_worker))

        # The objective is the sum of the costs
        objective = KIntVar(problem, "cost", objective_inf, objective_sup)
        problem.post(objective == sum(cost_matrix[worker][task] * worker_has_task[worker][task] for task in
                                      range(nb_task) for worker in range(nb_worker)))

        # Set the objective
        problem.setSense(KProblem.Minimize)
        problem.setObjective(objective)

        # Set the solver
        solver = KSolver(problem)

        # If the problem is infeasible
        if problem.propagate():
            # Display of various details to help find the source of the problem
            problem.display()
            problem.printMinimalConflictSet()
            print("Problem is infeasible")
            exit()

        # Launch the optimization
        result = solver.optimize()
        print("end result")
        if result:
            solution = problem.getSolution()
            # Display the solution
            for task in range(nb_task):
                for worker in range(nb_worker):
                    if solution.getValue(worker_has_task[worker][task]) == 1:
                        print(
                            f'Task {task} has been affected to worker {worker} 'f'with cost {cost_matrix[worker][task]}')
            print(f'Total cost : {solution.getValue(objective)}')

            # Return the objective
            problem.getSolution().display()
            return solution.getValue(objective)


    except ArtelysException as e:
        print(e)


if __name__ == '__main__':
    COST = [[90, 76, 75, 70, 50, 74],
            [35, 85, 55, 65, 48, 101],
            [125, 95, 90, 105, 59, 120],
            [45, 110, 95, 115, 104, 83],
            [60, 105, 80, 75, 59, 62],
            [45, 65, 110, 95, 47, 31],
            [38, 51, 107, 41, 69, 99],
            [47, 85, 57, 71, 92, 77],
            [39, 63, 97, 49, 118, 56],
            [47, 101, 71, 60, 88, 109],
            [17, 39, 103, 64, 61, 92],
            [101, 45, 83, 59, 92, 27]]

    ALLOWED_GROUPS = [[[2, 3], [1, 3], [1, 2], [0, 1], [0, 2]],
                      [[6, 7], [5, 7], [5, 6], [4, 5], [4, 7]],
                      [[10, 11], [9, 11], [9, 10], [8, 10], [8, 11]]]

    solve(COST, ALLOWED_GROUPS)