Assignment with teams of workers¶
Problem description¶
In this example, 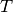 tasks must be assigned to
tasks must be assigned to 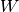 workers. The workers are divided into
workers. The workers are divided into 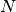 teams and each team can have
teams and each team can have 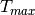 tasks assigned at most. Also, a single worker cannot be assigned to more than one task. The cost of a task is a function of the assigned worker.
tasks assigned at most. Also, a single worker cannot be assigned to more than one task. The cost of a task is a function of the assigned worker.
The aim is to minimize the total cost.
Naive modelling¶
The problem can be exposed as follows:
Let ![(X_{i,j})_{(i,j) \in [|1,T|]\times[|1,W|]}](../_images/math/45878f7e4939c69926ab76595d8d88bf26ef0bbe.png) be the set of binary variables indicating whether task
be the set of binary variables indicating whether task 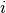 has been assigned to worker
has been assigned to worker 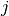 .
Let
.
Let ![TEAMS = (TEAM_{i})_{i \in [|1,N|]}](../_images/math/9d39d8a173207e301d506355fd2889ad5a6f2e28.png) with
with 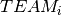 the set of integers representing the workers of team
the set of integers representing the workers of team 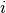 .
Let
.
Let ![C = (c_{i,j})_{(i,j) \in [|1,T|]\times[|1,W|]}](../_images/math/68eaf9e8dad7df12515a7da1cf839f6502afce6f.png) with
with 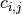 the cost associated with the assignment of task
the cost associated with the assignment of task 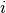 . to worker
. to worker 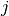 .
.
The problem is then:
![& \text{ minimize } \sum_{(i,j) \in [|1,T|]\times[|1,W|]} X_{i,j} \times c_{i,j} \\
& \\
& \text{ s.t } \\
&\forall i \in [|1,T|], \sum_{j \in [|1,W|]} X_{i,j} = 1 \\
&\forall j \in [|1,W|], \sum_{i \in [|1,T|]} X_{i,j} \leq 1 \\
&\forall t \in [|1,N|], \sum_{(i,j) \in [|1,T|] \times TEAM_{t}} X_{i,j} \leq T_{max}\\](../_images/math/4e01dc8248486cfd0767c98d5717d6e69f020cb7.png)
Implementation with standard API¶
The naive modelling could directly be implemented within Artelys Kalis solver. However, its large number of variables makes its resolution quite slow. By reducing this dimension, the following implementation improves drastically performance.
Previous modelling can be exposed as follows.
Let ![(W_{i})_{i \in [|1,W|]}](../_images/math/3bc488a5d18be48a16762527b196c4cecb4e3539.png) be the set of variables taking its values in
be the set of variables taking its values in ![[|1,T+1|]](../_images/math/6c8be48c409a33c73762378f8defff3852bd8cb2.png) indicating the task assigned to worker
indicating the task assigned to worker 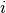 .
Task
.
Task 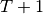 is a dummy task, representing the “no-affectation”. Cost of
is a dummy task, representing the “no-affectation”. Cost of 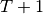 is
is  .
Let
.
Let ![TEAMS = (TEAM_{i})_{i \in [|1,N|]}](../_images/math/9d39d8a173207e301d506355fd2889ad5a6f2e28.png) be the set of teams with
be the set of teams with 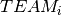 the set of integers corresponding to the workers of team
the set of integers corresponding to the workers of team 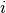 . Let matrix
. Let matrix ![C = (C_{i,j})_{(i,j) \in [|1,T+1|]\times[|1,W|]}](../_images/math/5c5ee689ec731fb81ed1c61aee924fd05da96c59.png) be the cost associated to each task and worker.
be the cost associated to each task and worker.
The Problem is:
![& \text{ minimize } \sum_{i \in [|1,T|]} C_{i,T_{i}} \\
& \\
& \text{ s.t } \\
&\forall i \in [|1,T|], |W_j = i|_{j \in [|1,T|]} = 1\\
&\forall t \in [|1,N|], |W_j = T+1|_{j \in TEAM_{t}} \ge |TEAM_{t}| - T_{max}](../_images/math/db2a66ee786912ff340ade7e972c9c0d13266e12.png)
The last constraint is the reciprocal of the naive modelling version : it asserts that enough workers in each team have been assigned to dummy task so not too many tasks are assigned to the team.
An implementation with Artelys Kalis is :
def solve(cost_matrix: list, teams_array: list, max_tasks_team: int): """ Resolution of the 'team_of_worker' problem """ # Get the number of tasks and workers from cost_matrix and the number of teams from teams_array nb_task = len(cost_matrix[1]) nb_worker = len(cost_matrix) nb_teams = len(teams_array) try: # Declaration of the problem session = KSession() problem = KProblem(session, "teams_of_worker") # Variables declaration workers_array = KIntVarArray() # Loop over the workers to initialise the variables giving the task assigned to each one of them. # Last task is idle. for worker in range(nb_worker): workers_array += KIntVar(problem, "Worker_{}".format(worker), 0, nb_task) # Assert that each task is assigned once for task in range(nb_task): problem.post(KOccurTerm(task, workers_array) == 1) # Assert that each team has at most max_tasks_team tasks teams_tasks = {team: KIntVarArray() for team in range(nb_teams)} # Loop over the teams to create a KIntVarArray for each of them in which are stored the tasks assigned to its # workers for team in range(nb_teams): for worker in teams_array[team]: teams_tasks[team] += workers_array[int(worker)] # Assert that enough workers have the fictitious task for the team to not have too much tasks problem.post(KOccurTerm(nb_task, teams_tasks[team]) >= len(teams_tasks[team]) - max_tasks_team) # Objective declaration # Transform the cost matrix into a Kalis object K_cost_matrix = KIntMatrix(nb_worker, nb_task + 1, 0, "cost") for worker in range(nb_worker): for task in range(nb_task): K_cost_matrix.setMatrix(worker, task, int(cost_matrix[worker][task])) # The objective will be greater than nb_task * the minimum of cost_matrix and lower than the sum of the # coefficients in cost_matrix objective_sup = sum(cost_matrix[worker][task] for task in range(nb_task) for worker in range(nb_worker)) objective_inf = nb_task * min( cost_matrix[worker][task] for task in range(nb_task) for worker in range(nb_worker)) # Transform the worker numbers into Kalis object to retrieve values from K_cost_matrix num_worker = KIntVarArray() for worker in range(nb_worker): num_worker += KIntVar(problem, "Num_{}".format(worker), 0, nb_worker) problem.post(num_worker[worker] == worker) # Get the cost of the workers given the tasks they have been assigned cost_worker = KIntVarArray() for worker in range(nb_worker): cost_worker += KIntVar(problem, "Cost_{}".format(worker), 0, int(max([max(cost_matrix[worker]) for worker in range(nb_worker)]))) kelt = KEltTerm2D(K_cost_matrix, num_worker[worker], workers_array[worker]) problem.post(KElement2D(kelt, cost_worker[worker])) # The objective is the sum of those costs objective = KIntVar(problem, "cost", objective_inf, objective_sup) problem.post(objective == sum(cost_worker[worker] for worker in range(nb_worker))) # Set the objective problem.setSense(KProblem.Minimize) problem.setObjective(objective) # Set the solver solver = KSolver(problem) # If the problem is infeasible if problem.propagate(): # Display various details to help find the source of the problem problem.display() problem.printMinimalConflictSet() print("Problem is infeasible") sys.exit(1) # Run optimization result = solver.optimize() if result: solution = problem.getSolution() # Display the solution for worker in range(nb_worker): if solution.getValue(workers_array[worker]) != nb_task: task = solution.getValue(workers_array[worker]) print(f'Task {task} has been affected to worker {worker} ' f'with cost {cost_matrix[worker][task]}') print(f'Total cost : {solution.getValue(objective)}') # Return the objective problem.getSolution().display() return solution.getValue(objective) except ArtelysException as e: print(e) if __name__ == '__main__': COST = [[90, 76, 75, 70], [35, 85, 55, 65], [125, 95, 90, 105], [45, 110, 95, 115], [60, 105, 80, 75], [45, 65, 110, 95]] TEAMS = [[0, 2, 4], [1, 3, 5]] TEAM_MAX = 2 solve(COST, TEAMS, TEAM_MAX)
Implementation with scheduling API¶
Even if the problem does not have a time dimension, it is possible to use the scheduling API to implement it. By considering a time period
of ![[0, W]](../_images/math/83c0f49fe2e4ccc0cbe4f2b28157998b588a748a.png) , with
, with 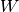 the number of workers, a single ressource with a capacity of 1, and
the number of workers, a single ressource with a capacity of 1, and 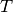 tasks, the
statment ‘task i start at j’ can be assimilated to the statment ‘task i has been assigned to worker j’.
tasks, the
statment ‘task i start at j’ can be assimilated to the statment ‘task i has been assigned to worker j’.
A possible way to implement this method is as follows :
def team_of_workers(cost_matrix: list, teams_array: list, max_tasks_team: int): """ Resolution of the 'team_of_worker' problem """ # Get the number of tasks and workers from cost_matrix and the number of teams from teams_array nb_task = len(cost_matrix[1]) nb_worker = len(cost_matrix) nb_teams = len(teams_array) try: # Declaration of the problem session = KSession() problem = KProblem(session, "teams_of_worker") # Creation of the schedule object with time horizon (0..nb_worker). The start date of a task will then be the # number of the worker it is allocated to schedule = KSchedule(problem, "schedule", 0, nb_worker) # Setting up the resources which are the workers. They are discrete but can only take up to one task workers = KDiscreteResource(schedule, "workers", 1) # Setting up the tasks. Each task has a length of 1 - it requires only one worker - and consume one # capacity of its worker tasks_array = KTaskArray() for task in range(nb_task): tasks_array += KTask(schedule, "task_{}".format(task), 1) tasks_array[task].requires(workers, 1) # Creation of an array linking a worker to its team team_array = KIntArray() for worker in range(nb_worker): for team in range(nb_teams): if worker in teams_array[team]: team_array.add(team) # Creation of an array giving the teams of each worker having a task team_of_task = KIntVarArray() worker_of_task = KIntVarArray() # Get the costs of the tasks given the worker they have been assigned to # Loop over the tasks to first get the workers it has been assigned to then store the team of the worker in # team_of_task for task in range(nb_task): team_of_task += KIntVar(problem, "team_of_task_{}".format(task), 0, nb_teams) worker_of_task += KIntVar(problem, "Worker_T_{}".format(task), 0, nb_worker) problem.post(worker_of_task[task] == tasks_array[task].getStartDateVar()) kelt = KEltTerm(team_array, worker_of_task[task]) problem.post(KElement(kelt, team_of_task[task])) # Assert that every team has max_tasks_team tasks at most for team in range(nb_teams): problem.post(KOccurTerm(team, team_of_task) <= max_tasks_team) # The objective will be greater than nb_task * the minimum of cost_matrix and lower than the sum of the # coefficients in cost_matrix objective_sup = sum(cost_matrix[worker][task] for task in range(nb_task) for worker in range(nb_worker)) objective_inf = nb_task * min( cost_matrix[worker][task] for task in range(nb_task) for worker in range(nb_worker)) # Get the cost of the tasks given the workers they are assigned to cost_task = KIntVarArray() K_cost_worker, K_elt = {}, {} for task in range(nb_task): K_cost_worker[task] = KIntArray() for worker in range(nb_worker): K_cost_worker[task] += int(cost_matrix[worker][task]) cost_task += KIntVar(problem, "Cost_{}".format(task), 0, max([cost_matrix[worker][task] for worker in range(nb_worker)])) K_elt[task] = KEltTerm(K_cost_worker[task], tasks_array[task].getStartDateVar()) problem.post(KElement(K_elt[task], cost_task[task])) # The objective is the sum of those costs objective = KIntVar(problem, "cost", objective_inf, objective_sup) problem.post(objective == sum(cost_task[task] for task in range(nb_task))) schedule.close() # Set the objective problem.setSense(KProblem.Minimize) problem.setObjective(objective) # Set the solver solver = KSolver(problem) # If the problem is infeasible if problem.propagate(): # Display various details to help find the source of the problem problem.display() problem.printMinimalConflictSet() print("Problem is infeasible") sys.exit(1) # Run optimization result = solver.optimize() if result: solution = problem.getSolution() # Display the solution for task in range(nb_task): print("Worker {} has task {}".format(solution.getValue(tasks_array[task].getStartDateVar()), task)) print('Total cost : ', solution.getValue(objective)) # Return the objective problem.getSolution().display() return solution.getValue(objective) except ArtelysException as e: print(e) if __name__ == '__main__': COST = [[90, 76, 75, 70], [35, 85, 55, 65], [125, 95, 90, 105], [45, 110, 95, 115], [60, 105, 80, 75], [45, 65, 110, 95]] TEAMS = [[0, 2, 4], [1, 3, 5]] TEAM_MAX = 2 team_of_workers(COST, TEAMS, TEAM_MAX)