Advanced Search Strategies

In this chapter, you will learn some advanced topics in order to better use Artelys Kalis. The following parts will be discussed:

• the methods involved in search control ;

• the creation of user-defined objects involved for search control.

KBranchingScheme, KVariableSelector and KValueSelector classes were introduced in chapter 5. The subject of this chapter will be the implementation of your own branching schemes, which requires a much deeper understanding of these classes.

Explanation and illustration of these concepts will be done in native language C++. The implementation for the Python and Java interfaces are detailed in last two sections. The whole mecanism is basically the same but some differences have been introduced due to inherent differences between languages.

A knapsack problem

First, we will describe a problem which will be used in the following parts of this chapter. This problem is the well-known Knapsack problem and is a very classic one in combinatorial optimization. The terms are the following: one has to choose some projects between several ones, each one involving expected revenue and an expected cost. You want to maximize the total expected revenue while keeping the total cost under a given maximum budget. Even with a problem whose formulation is so simple, it can be worth finding an appropriate branching scheme.

Here is a sample of program building an example with 39 projects:

C++PythonJava

try
{
    // *** Creation of the session
    KSession mySession;

    // *** Data definition
    const int nbConstraints = 1;

    //*** 39 variables
    const int nbProj = 39;
    int projValues[nbProj] = {560,1125,300,620,2100,431,68,328,47,122,322,196,41,25,425,4260,416,115,82,22,631,132,420,86,42,103,215,81,91,26,49,420,316,72,71,49,108,116,90};
    int constrCoeffs[nbConstraints][nbProj] = { { 40,91,10,30,160,20,3,12,3,18,9,25,1,1,10,280,10,8,1,1,49,8,21,6,1,5,10,8,2,1,0,10,42,6,4,8,0,10,1} };
    int constrRHS[nbConstraints] = { 600 };

    // *** Creation of the problem in this session (hold no more than 1000 variables)
    KProblem knapsack(mySession,"Knapsack");

    // *** 0-1 Variables to choose or not choose a project
    KIntVarArray projectChosen(knapsack,nbProj,0,1,"projChoose");

    // *** Posting constraints to the problem
    for (int constrIndex = 0; constrIndex < nbConstraints; constrIndex++)
    {
        KLinTerm l;
        for (int projIndex = 0; projIndex < nbProj; projIndex++)
        {
            l = l + constrCoeffs[constrIndex][projIndex] * projectChosen[projIndex];
        }
        knapsack.post((l <= constrRHS[constrIndex]));
    }

    for(int i = 0; i < nbProj; i++)
    {
        for(int j = i+1; j < nbProj; j++)
        {
            if ((projValues[i] == projValues[j]) && (constrCoeffs[0][i] == constrCoeffs[0][j]))
            {
                printf("Equivalent tasks: %d and %d\n",i,j);
                knapsack.post( projectChosen[i] >= projectChosen[j]);
            }
        }
    }

    // *** Definition of our objective function
    KLinTerm myObjective;
    for (int projIndex = 0; projIndex < nbProj; projIndex++)
    {
        myObjective = myObjective + projValues[projIndex]*projectChosen[projIndex];
    }

    KIntVar overallRevenue(knapsack, "Objective", 0, 20000);
    knapsack.post(overallRevenue == myObjective);

    // *** We want to maximize the overall revenue
    knapsack.setObjective(overallRevenue);
    knapsack.setSense(KProblem::Maximize);

    // *** Definition of our branching strategy
    KBranchingSchemeArray myBranchingScheme;
    myBranchingScheme += KnapsackAssignVar(KnapsackVarSelector(nbProj,projValues,constrCoeffs[0]), OneBeforeZero(), &projectChosen);

    // *** Creation of the solver that make good use of our branching strategy
    KSolver mySolver(knapsack, myBranchingScheme);

    // *** Optimize without restart
    mySolver.optimize(false);

    // *** Printing some statistics about the search
    cout << "Number of solutions found: " << knapsack.getNumberOfSolutions() << endl;
    cout << "Best solution objective value: " << knapsack.getSolution().getObjectiveValue() << endl;
    cout << "Best solution found at: " << knapsack.getSolution().getIntAttrib(KSolution::NumberOfNodes) << endl;
    cout << "Number of nodes: " << mySolver.getIntAttrib(KSolver::NumberOfNodes) << endl;
    cout << "Projects are: " << endl;
    mySolver.printStats();

    // *** Show the solution
    knapsack.getSolution().print();
}
catch (ArtelysException& artelysException)
{
    // *** An error occured
    cout << "Exception " << artelysException.getCode() << " raised: " << artelysException.getMessage() << endl;
}

The variables of the problem are hold in projChosen: they are named “projChosen0”, …, “projChosen27” and take the value 0 if the problem is not chosen, 1 if the problem is chosen.

The total cost is computed in the KLinTerm object totCost. KLinTerm is the class representing linear expressions: we use the overloaded += operator in order to build totCost. For each project, the cost of the project projCost[projIndex] is added to the total cost if the project is chosen, i.e. if projChosen[projIndex] takes the value 1. The constraint of maximal budget is then built with the overloaded <= operator.

The total revenue is computed the same way and is set as objective of the optimization.

The KValueSelector class (C++ implementation)

A KValueSelector is an object in charge of providing one value corresponding to a variable given as a parameter. This section will show how to create a new class inheriting from KValueSelector. This class will be OneBeforeZero. For the knapsack problem, all variables are binary and this selector will just choose the value one if it is still in domain else zero. It has the same behavior as KMaxToMin in the case of binary variables.

First of all, here are the methods that must be implemented in your class:

• at least one main constructor, which will be used in the programs based on your KValueSelector ;

• a copy-constructor ;

• virtual int selectNextValue(KIntVar* intVar): this method is in charge of computing a value considering current state of the variable given in parameter ;

• virtual KValueSelector* getCopyPtr() const: this method is called by Artelys Kalis for internal memory management purposes. It must contains a unique statement: return new YourClass(*this); where YourClass is the name of your selector’s class. It returns a pointer to a copy of the current object. You do not need to manage this pointer: the library will do it.

Here is the declaration of the class:

C++

class OneBeforeZero: public KValueSelector
{
    public:
        // Constructors
        OneBeforeZero();

        // Copy constructor
        OneBeforeZero(const OneBeforeZero& oneBeforeZeroToCopy);

        // Destructor
        ~OneBeforeZero();

        //methods
        virtual int selectNextValue(KIntVar* intVar); // get Next Value
        virtual KValueSelector* getCopyPtr() const;
};

The implementation is rather simple in this case, nothing special must be done for constructors and destructors. Only the selectNextValue() method requires a specific code. For the interfaces Python and Java, the implementation is also rather simple for the class and definition of the selectNextValue() method.

C++

int OneBeforeZero::selectNextValue(KIntVar* intVar)
{
    if (intVar->canBeInstantiatedTo(1))
    {
        return 1;
    }
    else
    {
        return 0;
    }
}

The KVariableSelector class (C++ implementation)

The KVariableSelector must select one variable among a list of possible variables given as a parameter. This section will show how to create a new class inheriting from KValueSelector. This class will be named KnapsackVarSelector. In fact, it is based on an often-used greedy heuristic. You incorporate the variable Xk which is verifying:

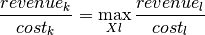
First of all, here are the methods that must be implemented in your class:

• at least one main constructor, which will be used in the programs based on your KVariableSelector ;

• a copy-constructor ;

• the destructor ;

• virtual KIntVar* selectNextVariable(KIntVarArray* intVarArray): this method is in charge of selecting a variable in the list intVarArray ;

• virtual KValueSelector* getCopyPtr() const: this method is called by Artelys Kalis for internal memory management purposes. It must contain a unique statement: return new YourClass(*this); where YourClass is the name of your selector’s class. It returns a pointer to a copy of the current object. You do not need to manage this pointer: the library will do it.

Here is the declaration of the class:

C++

class KnapsackVarSelector: public KVariableSelector
{
    private:
        int _nbVar;
        double* _ratios;

    public:
        // Constructors
        KnapsackVarSelector(const int nbVar, const int *values, const int *costs);
        KnapsackVarSelector(const KnapsackVarSelector &knapsackVarSelectorToCopy);

        // Destructor
        virtual ~KnapsackVarSelector();

        // get Next Variable
        virtual KIntVar* selectNextVariable(KIntVarArray* intVarArray);
        virtual KVariableSelector* getCopyPtr() const;
};

The array _ratios will be initialized in the constructor:

C++

KnapsackVarSelector::KnapsackVarSelector(const int nbVar, const int *values, const int *costs)
{
    int variableIndex;

    _nbVar = nbVar;
    _ratios = new double[_nbVar];

    for (variableIndex = 0; variableIndex < nbVar; variableIndex++)
    {
        _ratios[variableIndex] = (costs[variableIndex] == 0 ? MAX_DOUBLE: values[variableIndex] / 1.0);
    }
}

Copy constructor and destructor will contain a simple code managing mainly the array _ratios.

The main method is the selection method:

C++

KIntVar* KnapsackVarSelector::selectNextVariable(KIntVarArray* intVarArray)
{
    int variableIndex;
    double bestRatio = -MAX_DOUBLE;
    KIntVar *currentIntVar;
    KIntVar *result = NULL;

    for (variableIndex = 0; variableIndex < intVarArray->getNumberOfElements(); variableIndex++)
    {
        currentIntVar = intVarArray->getElt(variableIndex);
        if (!currentIntVar->getIsInstantiated())
        {
            if (_ratios[variableIndex] > bestRatio)
            {
                bestRatio = _ratios[variableIndex];
                result = currentIntVar;
            }
        }
    }

    return result;
}

This method is looking for an unassigned variable with the biggest ratio.

The KBranchingScheme class (C++ implementation)

The KBranchingScheme class represents branching schemes in which any number of branches are built at each expanded node. When implementing your own branching schemes, it is recommended to make it inheriting from this class.

Here are the methods that must be implemented in your class. It also explains most of them through the example of KAssignVar for a better understanding:

class KBranchingScheme

• At least one main constructor, which will be used in the programs based on your KBranchingScheme.

• A copy-constructor.

• The destructor.

selectNextBranchingObject()

This method returns the object which will be used to branch at the current node. By object, we mean mainly variables, set of variables, constraints, or set of constraints. For example, the KAssignVar scheme branch on unassigned variables: the selectNextBranchingObject() of this class then returns KIntVar pointers.

getNextBranch()

Returns the branching information used to identify the next branch to be built. For KAssignVar, this will be the value to which the variable has to be instantiated.

finishedBranching()

This method returns true if there is no more branch to be built, false else. Its parameters are: the current branching object, branching information and the branch number (number starts at one). We will show below that KAssignVar only uses the KIntVar branching object.

goDownBranch()

This method builds a new branch by performing all needed operations on the branching object. In KAssignVar for example, this method will instantiate the variable stored in branchingObject to the value stored in branchingInformation.

goUpBranch()

Unsurprisingly, this method performs the operations needed when the algorithm comes back to the parent node. In the case of KAssignVar, it will remove the value to which the variable has been instantiated when branching from the domain of the variable. All the solutions where this variable takes this value have been explored in the branch, so there is no need to let this value in the domain at the parent node.

freeAllocatedObjectsForBranching()

This method is used to free the branching object and/or the branching information if they have been allocated dynamically in the getNextBranch() and selectNextBranchingObject() methods.

getCopyPtr()

This method is called by Artelys Kalis for internal memory management purposes. It must contains a unique statement: return new YourClass(*this); where YourClass is the name of your scheme’s class. It returns a pointer to a copy of the current object. You do not need to manage this pointer: the library will do it.

getCopyPtr(KProblem* problem)

This method is called by Artelys Kalis for internal memory management between KProblem instances and KSolver workers . It must contains a unique statement: return new YourClass(/*...*/); where YourClass is the name of your scheme’s class. It returns a pointer to an instance copy of the current object. You do not need to manage this pointer: the library will do it. The arguments are depending on the implementation of YourClass, but in general it contains a variable selector, a value selector, and a variable array. It is mandatory to obtain an instance copy of all the variable involved in the branching scheme by calling one of the KProblem::getCopyPtr() methods, typically KProblem::getCopyPtr(const KIntVarArray*).

In order to see how it could be implemented, we will present a simple version of KAssignVar working with our two new classes: OneToZero and KnapsackVarSelector. It will be called KnapsackAssignVar. We will give it two selectors and a list of variables. Then, it will be in charge of producing all nodes in our tree search algorithm. All methods will be written but you may prefer to specialize an existing KBranchingScheme. In that case, only few methods will need to be written. We make KnapsackAssignVar inheriting from KBranchingScheme in order to be more general, even if only two sub-nodes will be created each time.

Here is the declaration of the class:

C++

class KnapsackAssignVar: public KBranchingScheme
{
    protected:
        KIntVarArray* _intVarArray;
        KnapsackVarSelector* _kvs;
        OneBeforeZero* _obz;

    public:
        // Constructor
        KnapsackAssignVar(const KnapsackVarSelector& varSel, const OneBeforeZero& valSel, KIntVarArray* intVarArray);

        // Copy constructor
        KnapsackAssignVar(const KnapsackAssignVar& knapsackAssignVarToCopy);

        // Destructor
        ~KnapsackAssignVar();

        //methods
        virtual void* selectNextBranchingObject(); // get Next Branching Object
        virtual bool finishedBranching(void* branchingObject, void* branchingInformation, int currentBranchNumber);
        virtual void* getNextBranch(void* branchingObject, void* branchingInformation, int currentBranchNumber);
        virtual void goDownBranch(void* branchingObject, void* branchingInformation, int currentBranchNumber);
        virtual void goUpBranch(void* branchingObject, void* branchingInformation, int currentBranchNumber);
        virtual void freeAllocatedObjectsForBranching(void* branchingObject, void* branchingInformation);
        virtual KBranchingScheme* getCopyPtr() const;
        virtual KBranchingScheme* getCopyPtr(KProblem* problem) const;
};

There is only one main constructor: it allows to specify the variable selector, the value selector and the involved variables. All other methods are those that we have listed above.

Here is the implementation of the constructor:

C++

KnapsackAssignVar::KnapsackAssignVar(const KnapsackVarSelector& varSel, const OneBeforeZero& valSel, KIntVarArray* intVarArray): KBranchingScheme()
{
    _kvs = (KnapsackVarSelector*) varSel.getCopyPtr();
    _obz = (OneBeforeZero*) valSel.getCopyPtr();
    _intVarArray = intVarArray;
}

We make copy of constructors but the array of variables is given through a pointer and is kept in the same form in KnapsackAssignVar.

The main work is made on the different methods explaining the way branching will be made. The global source code is given above:

C++

void* KnapsackAssignVar::selectNextBranchingObject()
{
    return _kvs->selectNextVariable(_intVarArray);
}

bool KnapsackAssignVar::finishedBranching(void* branchingObject,void* branchingInformation,int currentBranchNumber)
{
    return (currentBranchNumber == 2);
}

void* KnapsackAssignVar::getNextBranch(void* branchingObject,void* branchingInformation,int currentBranchNumber)
{
    int nextValue = _obz->selectNextValue((KIntVar*) branchingObject);
    return new int(nextValue);
}

void KnapsackAssignVar::goDownBranch(void* branchingObject,void* branchingInformation,int currentBranchNumber)
{
    ((KIntVar*) branchingObject)->instantiate((*((int*) branchingInformation)));
}

void KnapsackAssignVar::goUpBranch(void* branchingObject,void* branchingInformation,int currentBranchNumber)
{
    ((KIntVar*) branchingObject)->remVal((*((int*) branchingInformation)));
}

void KnapsackAssignVar::freeAllocatedObjectsForBranching(void* branchingObject,void* branchingInformation)
{
    int* nextValue = (int*) branchingInformation;
    if (nextValue)
    {
        delete nextValue;
    }
}

Three remarks must be made:

• currentBranchNumber is initialized with 0. First branch will be number 1, second will be number 2, … ;

• in order to work on all types of objects and stay generic, we always work with undefined pointers. This has a drawback that requires some attention when writing your application: you often have to cast branchingObject and branchingInformation in the real type you require ;

• last assigned value is removed when you go up from one node to its parent. You may prefer to go back and test the remaining value. In this case, you will not be able to use the KValueSelector because no value has been removed from the domain. Your code may become:

C++

void KnapsackAssignVar::goDownBranch(void* branchingObject,void* branchingInformation,int currentBranchNumber)
{
    if (currentBranchNumber == 1)
    {
        ((KIntVar*) branchingObject)->instantiate(1);
    }
    else
    {
        ((KIntVar*) branchingObject)->instantiate(0);
    }
}

void KnapsackAssignVar::goUpBranch(void* branchingObject,void* branchingInformation,int currentBranchNumber) {}

It has few impact here but if there were more branches, some of them may have been pruned quickly while removing values already tested.

In order to show the efficiency of doing such a work, we made a small comparison between default branching schemes, this one and a last one for which we modified the KVariableSelector by looking for the variable with the highest value, here are the results:

Branching Scheme	Node of the best solution	Total number of nodes	Number of solutions found
Default Branching Scheme	3110	4045	147
KnapsackAssignVar	28	27534	3
KnapsackAssignVar with different KVariableSelector	63	508	4

KnapsackAssignVar is going very quickly to the optimal solution. Depending on the KVariableSelector, it may require more nodes to prove optimality.

An advanced strategy for the Knapsack problem : the Python interface implementation

The concepts are similar to ones presented above. An advanced strategy will implement a branching scheme which can be defined through a variable selector and a value selector.

KValueSelector

As explained before a KValueSelector is an object in charge of providing one value corresponding to a variable given as a parameter. Methods that must be implemented in your class are listed below:

• at least one main constructor, which will be used in the programs based on your KValueSelector. Main constructor needs to have a reference to the current KProblem object solved in its argument ;

• a copy-constructor ;

• int selectNextValue(KIntVar intVar): this method is in charge of computing a value considering current state of the variable given in parameter ;

• getCopyPtr: this method is called by Artelys Kalis for internal memory management purposes. It must contains a unique statement: return new YourClass(*this); where YourClass is the name of your selector’s class. It returns a pointer to a copy of the current object.

Here is the declaration of the class:

Python

class OneBeforeZero(KValueSelector):
    def __init__(self,problem):
        """Constructor of the value selector"""
        super(OneBeforeZero,self).__init__(problem)

    def selectNextValue(self, intVar):
        if intVar.canBeInstantiatedTo(1):
            return intVar.getSup()
        else:
            return intVar.getInf()

KVariableSelector

The KVariableSelector must select one variable among a list of possible variables given as a parameter. Methods that must be implemented in your class are :

• at least one main constructor, which will be used in the programs based on your KVariableSelector. Main constructor needs to have a reference to the current KProblem object solved in its argument ;

• a copy-constructor ;

• selectNextVariable(KIntVarArray int_var_array): this method is in charge of selecting a variable in the list int_var_array ;

• getCopyPtr: this method is called by Artelys Kalis for internal memory management purposes. It must contain a unique statement: return new YourClass(*this); where YourClass is the name of your selector’s class. It returns a pointer to a copy of the current object.

Here is the declaration of the class:

Python

class KnapsackVarSelector(KVariableSelector):
    def __init__(self, nbVars, values, weights,problem):
        """Constructor of the knapsack variable selector"""
        super(KnapsackVarSelector,self).__init__(problem)
        self.nbVars = nbVars
        self.values = values
        self.weights = weights
        self.ratios = [sys.float_info.max] * self.nbVars
        for variableIndex in range(self.nbVars):
            if weights[variableIndex] != 0:
                self.ratios[variableIndex] = values[variableIndex]

    def selectNextVariable(self, int_var_array):
        """Implmentation of the virtual method for selecting the next variable"""
        bestRatio = -sys.float_info.max
        result = None

        for i in range(int_var_array.getNumberOfElements()):
            currentIntVar = int_var_array.getElt(i)
            if not currentIntVar.getIsInstantiated():
                if self.ratios[i] > bestRatio:
                    bestRatio = self.ratios[i]
                    result = currentIntVar

        return result

KIntVarBranchingScheme or KFloatVarBranchingScheme

A branching scheme defines in which any number of branches are built at each expanded node. This concept is defined in Python through an object that defined the type of object we will branch on. More precisely, for an integer variable a KIntVarBranchingScheme needs to be implemented and for a continuous variable a KFloatVarBranchingScheme

Here are the methods that must be implemented in your class :

• at least one main constructor, which will be used in the programs based on your KBranchingScheme. Main constructor needs to have a reference to the current KProblem object solved in its argument ;

• a copy-constructor.

selectNextBranchingVar()

This method returns the KIntVar variable which will be used to branch at the current node.

getNextBranch()

Returns an integer pointer to the branching information used to identify the next branch to be built.

finishedBranching()

This method returns true if there is no more branch to be built, false else. Its parameters are: the current branching object, branching information and the branch number (number starts at one).

goDownBranch()

This method builds a new branch by performing all needed operations on the branching object.

goUpBranch()

Unsurprisingly, this method performs the operations needed when the algorithm comes back to the parent node.

freeAllocatedObjectsForBranching()

This method is used to free the branching object and/or the branching information if they have been allocated dynamically in the getNextBranch() and selectNextBranchingObject() methods.

getCopyPtr()

This method is called by Artelys Kalis for internal memory management purposes. It must contains a unique statement: return new YourClass(*this); where YourClass is the name of your scheme’s class. It returns a pointer to a copy of the current object. You do not need to manage this pointer: the library will do it.

getCopyPtr(KProblem* problem)

This method is called by Artelys Kalis for internal memory management between KProblem instances and KSolver workers . It must contains a unique statement: return new YourClass(/*...*/); where YourClass is the name of your scheme’s class. It returns a pointer to an instance copy of the current object. You do not need to manage this pointer: the library will do it. The arguments are depending on the implementation of YourClass, but in general it contains a variable selector, a value selector, and a variable array. It is mandatory to obtain an instance copy of all the variable involved in the branching scheme by calling one of the KProblem::getCopyPtr() methods, typically KProblem::getCopyPtr(const KIntVarArray*).

Warning

The branching information is an integer pointer. In the interface Python, it needs to be treated as, and casted into an integer if necessary. The following methods allow the user to do so, and the examples make use of it :

• intp = new_intp create a new integer pointer ;

• intp_assign(intp, value) assign a value to an integer pointer ;

• value = intp_value(intp) retrieve the integer value of an integer pointer ;

• delete_intp(intp) delete an integer pointer.

class KnapsackAssignVar(KIntVarBranchingScheme): def __init__(self, var_sel, val_sel, int_var_array): “””Constructor of the branching scheme””” super(KnapsackAssignVar, self).__init__(int_var_array.getElt(0).getProblem()) self._kvs = var_sel self._obz = val_sel self._int_var_array = int_var_array

    def selectNextBranchingVar(self):
        return self._kvs.selectNextVariable(self._int_var_array)

    def finishedBranching(self, branching_object, branching_info, current_branch_number):
        return (current_branch_number == 2)

    def getNextBranch(self, branching_object, branching_info, current_branch_number):
        value = int(self._obz.selectNextValue(branching_object))

        intp = new_intp()
        intp_assign(intp, value)

        return intp

    def goDownBranch(self, branching_object, branching_info, current_branch_number):
        value = intp_value(branching_info)

        branching_object.instantiate(value)

    def goUpBranch(self, branching_object, branching_info, current_branch_number):
        value = intp_value(branching_info)

        branching_object.remVal(value)

    def freeAllocatedObjectsForBranching(self, branching_object, branching_info):
        delete_intp(branching_object)

    def getCopyPtr(self):
        """Obtain a copy of the constraint"""
        return KnapsackAssignVar(self._kvs, self._obz, self._int_var_array)

    def getInstanceCopyPtr(self, *args):
        """Obtain an instance copy of the constraint"""
        problem = args[0]
        return KnapsackAssignVar(self._kvs, self._obz, problem.getInstanceOf(self._int_var_array))

The complete implementation of the Knapsack problem and the advanced strategy is :

from kalis import * import sys

class OneBeforeZero(KValueSelector):
    def __init__(self,problem):
        """Constructor of the value selector"""
        super(OneBeforeZero,self).__init__(problem)

    def selectNextValue(self, intVar):
        if intVar.canBeInstantiatedTo(1):
            return intVar.getSup()
        else:
            return intVar.getInf()

class KnapsackVarSelector(KVariableSelector):
    def __init__(self, nbVars, values, weights,problem):
        """Constructor of the knapsack variable selector"""
        super(KnapsackVarSelector,self).__init__(problem)
        self.nbVars = nbVars
        self.values = values
        self.weights = weights
        self.ratios = [sys.float_info.max] * self.nbVars
        for variableIndex in range(self.nbVars):
            if weights[variableIndex] != 0:
                self.ratios[variableIndex] = values[variableIndex]

    def selectNextVariable(self, int_var_array):
        """Implmentation of the virtual method for selecting the next variable"""
        bestRatio = -sys.float_info.max
        result = None

        for i in range(int_var_array.getNumberOfElements()):
            currentIntVar = int_var_array.getElt(i)
            if not currentIntVar.getIsInstantiated():
                if self.ratios[i] > bestRatio:
                    bestRatio = self.ratios[i]
                    result = currentIntVar

        return result

    def getCopyPtr(self):
        """Obtain a copy of the constraint"""
        return KnapsackVarSelector(self.nbVars, self.values, self.weights)


class KnapsackAssignVar(KIntVarBranchingScheme):
    def __init__(self, var_sel, val_sel, int_var_array):
        """Constructor of the branching scheme"""
        super(KnapsackAssignVar, self).__init__(int_var_array.getElt(0).getProblem())
        self._kvs = var_sel
        self._obz = val_sel
        self._int_var_array = int_var_array

    def selectNextBranchingVar(self):
        return self._kvs.selectNextVariable(self._int_var_array)

    def finishedBranching(self, branching_object, branching_info, current_branch_number):
        return (current_branch_number == 2)

    def getNextBranch(self, branching_object, branching_info, current_branch_number):
        value = int(self._obz.selectNextValue(branching_object))

        intp = new_intp()
        intp_assign(intp, value)

        return intp

    def goDownBranch(self, branching_object, branching_info, current_branch_number):
        value = intp_value(branching_info)
        branching_object.instantiate(value)

    def goUpBranch(self, branching_object, branching_info, current_branch_number):
        value = intp_value(branching_info)
        branching_object.remVal(value)

    def freeAllocatedObjectsForBranching(self, branching_object, branching_info):
        delete_intp(branching_object)

    def getCopyPtr(self):
        """Obtain a copy of the constraint"""
        return KnapsackAssignVar(self._kvs, self._obz, self._int_var_array)

    def getInstanceCopyPtr(self, *args):
        """Obtain an instance copy of the constraint"""
        problem = args[0]
        return KnapsackAssignVar(self._kvs, self._obz, problem.getInstanceOf(self._int_var_array))


mySession = KSession()

nbConstraints = 1

# 39 variables
nbProj = 39
projValues = [560, 1125, 300, 620, 2100, 431, 68, 328, 47, 122, 322, 196, 41, 25, 425, 4260, 416, 115, 82, 22, 631, 132, 420, 86, 42, 103, 215, 81, 91, 26, 49, 420, 316, 72, 71, 49, 108, 116, 90]
constrCoeffs = [[ 40, 91, 10, 30, 160, 20, 3, 12, 3, 18, 9, 25, 1, 1, 10, 280, 10, 8, 1, 1, 49, 8, 21, 6, 1, 5, 10, 8, 2, 1, 0, 10, 42, 6, 4, 8, 0, 10, 1]]
constrRHS = [600]

# Creation of the problem in this session (hold no more than 1000 variables)
knapsack = KProblem(mySession, "Knapsack")

# 0-1 Variables to choose or not choose a project
projectChosen = KIntVarArray(knapsack, nbProj, 0, 1, "projChoose")

# Posting constraints to the problem
for constrIndex in range(nbConstraints):
    total_volume = sum(constrCoeffs[constrIndex][projIndex] * projectChosen[projIndex] for projIndex in range(nbProj))
    knapsack.post((total_volume <= constrRHS[constrIndex]))

# Symmetry removal
for i in range(nbProj):
    for j in range(i + 1, nbProj):
        if (projValues[i] == projValues[j]) & (constrCoeffs[0][i] == constrCoeffs[0][j]):
            print("Equivalent tasks: %d and %d" % (i, j))
            knapsack.post(projectChosen[i] >= projectChosen[j])

# Definition of our objective function
overallRevenue = KIntVar(knapsack, "Objective", 0, 20000)
knapsack.post(overallRevenue == sum(projValues[projIndex] * projectChosen[projIndex] for projIndex in range(nbProj)))

# We want to maximize the overall revenue
knapsack.setObjective(overallRevenue)
knapsack.setSense(KProblem.Maximize)

# Definition of our branching strategy
myBranchingScheme = KBranchingSchemeArray()
myBranchingScheme += KnapsackAssignVar(KnapsackVarSelector(nbProj, projValues, constrCoeffs[0],knapsack), OneBeforeZero(knapsack), projectChosen)

# Creation of the solver that make good use of our branching strategy
mySolver = KSolver(knapsack, myBranchingScheme)

# Optimize without restart
mySolver.optimize(False)

# Printing some statistics about the search
print("Number of solutions found: %d" % knapsack.getNumberOfSolutions())
print("Best solution objective value: %d" % knapsack.getSolution().getObjectiveValue())
print("Best solution found at: %d" % knapsack.getSolution().getIntAttrib(KSolver.NumberOfNodes))
print("Number of nodes: %d" % mySolver.getIntAttrib(KSolver.NumberOfNodes))
print("Projects are: ")
knapsack.getSolution().display()