Glossary¶

Attribute¶

A property of a solution or search process which is computed while optimizing and looking for solutions. It mainly provides information on the number of nodes, time spent and depth of the tree search.

Branch and bound¶

Branch and bound (B&B) is a general algorithm for finding optimal solutions of various optimization problems, especially in discrete and combinatorial optimization. It consists of a systematic enumeration of all candidate solutions, where large subsets of fruitless candidates are discarded en masse, by using upper and lower estimated bounds of the quantity being optimized.

The method was first proposed by A. H. Land and A. G. Doig in 1960 for linear programming.

Branching scheme¶

An object which is in charge of constructing sub-problems at each node of the tree search. It manages the way these new nodes will be built.

Consistent instantiation¶

Consistent instantiation of a constraint network is an instantiation of the variables such that the constraints between variables are satisfied, also called admissible/satisfied instantiation, consistent assignment of values, or consistent labeling. Solution is often used as a synonym for consistent instantiation, but may also denote the result after applying any (local/partial) consistency algorithm.

Consistency techniques and constraint propagation¶

Consistency algorithms remove inconsistent values from the domains of variables. Informally speaking, a consistency algorithm is ‘stronger’ than another one if it reduces the domains further, i.e., it establishes a higher level of consistency. In finite domain CP, typically local consistency algorithms are used. Local or partial consistency signifies that only subsets of the constraints of a system of constraints are simultaneously satisfied. A locally consistent (according to some notion of consistency, such as arc-consistency) constraint network can be obtained by propagating iteratively the effects of each constraint to all other constraints it is connected to through its variables until a stable state is reached. This process is referred to as constraint propagation. Propagation properties of constraints vary, e.g., due to their implementation, or the types of variables used. Possible events triggering their evaluation may be variable instantiation, modification of domain bounds, removing of value(s) from a domain, etc.

Constraint¶

A relation over a set of variables limiting the combination of values that these variables can take; constraints may also be interpreted as mappings from the domains of the variables onto the Boolean values true and false. A (conceptual) constraint can sometimes be implemented in different ways enforcing various levels of consistency (see below) with different computational overhead. So-called global constraints subsume a set of other constraints (for instance an all-different relation on a set of variables replaces pair wise disequality constraints). Global constraints use specific propagation/consistency algorithms that render them more efficient than the set of constraints they replace.

Constraint programming¶

A technology solving decision and optimization problems by means of variables and constraints and using constraint propagation associated to tree search for the solving process.

Constraint solver¶

(Also: constraint engine.) Distinction between exact and incomplete solvers. Exact solvers guarantee the satisfiability of the system of constraints at any stage of the computations, they usually work on rational numbers (trees of rationals and linear constraints). Incomplete solvers are designed for more complex domains such as integers where checking and maintaining consistency of the overall system is too expensive or not possible with presently known algorithms. These solvers work with simplified calculations establishing some sort of partial (local) consistency among constraints; usually simply stating constraints does not produce a solution, an enumeration phase (searching for solutions) is necessary.

Constraint solving¶

Deciding the consistency or satisfiability of a system of constraints.

Constraint type¶

There are many types of constraints. We can classify them in four main types:

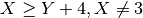
arithmetic : $X \geq Y+4, X \ne 3$

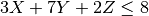
linear : $3X + 7Y +2Z \leq 8$

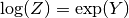
non linear : $\log(Z) = \exp(Y)$

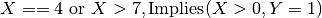
logical : $X==4 \text{ or } X > 7, \text{Implies}(X>0,Y=1)$

semantic : Element, AllDifferent, Occurence, Cardinality.

Control¶

A parameter of the solver whose value limits or influences the solution process.

Domain¶

The set of values (also: labels) a variable may take. In Xpress-Kalis, it may consist of discrete values, or intervals of integers. When solving CP problems active use of the domain concept is made. At any stage, the domain of a variable is the set of values that cannot be proved to be inconsistent (with the constraints on this variable) using the available consistency checking methods. Assigning or restricting domains is often interpreted as unary constraints on the corresponding variables.

Finite domain constraint problem/constraint satisfaction problem (CSP)¶

Defined by a finite set of variables taking values from finite domains and a (conjunctive) set of constraints on these variables. The objective may be either finding one solution (any or an optimal) or all solutions (consistent assignment of values to the variables so that all the constraints are satisfied simultaneously) for the given instance. The term constraint network is frequently employed to denote CP problems in allusion to the graphical representation as a hyper graph (constraint graph), where nodes represent variables, and constraints are (hyper) arcs linking several nodes. There is no standard problem representation in CP.

Global constraint¶

A constraint involving many variables which has a higher level of consistency achieved by the propagation engine. Thanks to the semantic of the “global constraint” and specific propagation based on this semantic, stronger propagation will be made compared to the same problem modeled by a set of local constraints (providing a hope for smaller search trees).

Instantiation¶

Instantiation of a set of variables is an assignment of a value to each variable from its domain,also called labeling of each variable with a value from its domain.

Integer variable¶

A decision variable that may take only integer values in solutions.

Linear Programming¶

Linear programming (LP) is a mathematical method for determining a way to achieve the best outcome (such as maximum profit or lowest cost) in a given mathematical model for some list of requirements represented as linear equations.

Local Search¶

local search is a metaheuristic for solving computationally hard optimization problems. Local search can be used on problems that can be formulated as finding a solution maximizing a criterion among a number of candidate solutions. Local search algorithms move from solution to solution in the space of candidate solutions (the search space) until a solution deemed optimal is found or a time bound is elapsed

Meta Heuristic¶

A metaheuristic is a heuristic method for solving a very general class of computational problems by combining user-given black-box procedures — usually heuristics themselves — in the hope of obtaining a more efficient or more robust procedure. The name combines the Greek prefix “meta” (“beyond”, here in the sense of “higher level”) and “heuristic” (“to find”).

Model¶

A CP model specifies all variables, their domains and their declarative meaning and conceptual constraints imposed on them (as opposed to actual constraints that are used to implement the properties of the solution and the search process). In CP in general, a model preserves much problem-specific knowledge about variables and the relations between them. This allows the development and application of more efficient specialized solution strategies.

Objective¶

A linear term which is to be optimized (maximized or minimized) by choosing values for the decision variables.

Optimal solution¶

A solution that gives the best possible value for the objective.

Optimization¶

In mathematics and computer science, optimization refers to choosing the best element from some set of available alternatives.

Partial search¶

A tree search process which is not visiting all necessary nodes. It means that, when looking for a solution, some nodes are not visited and, when optimizing a problem, some nodes are pruned whereas they may give a better solution.

Problem¶

A set of variables and constraints on these variables, and possibly an objective. It represents the entity for which we are trying to find solutions or optimal solutions.

Propagation¶

The activity of deducing information from the current state of variables and constraints. Propagation is triggered whenever the state of the problem is modified (adding a constraint, changing variable domain values) and this information is given (propagated) to the constraint and variables that may deduce other things.

Redundant constraint¶

A constraint is redundant with respect to a set of constraints, if it is satisfied when the set of constraints is satisfied. Although redundant constraints do not change the set of solutions (consistent instantiations) of a problem, in practice it may be useful to add redundant constraints to the model formulation because they can help CP solution procedures, particularly by achieving more powerful constraint propagation.

Relaxations¶

A relaxation technique is a method in mathematical optimization for relaxing a strict requirement, by either substituting for it another more easily handled requirement or else dropping it completely. Relaxation techniques are commonly used in place of branch and bound algorithms, or to obtain bounds in those algorithms.

Scheduling¶

Scheduling is an important tool for manufacturing and engineering, where it can have a major impact on the productivity of a process. In manufacturing, the purpose of scheduling is to minimize the production time and costs, by telling a production facility what to make, when, with which staff, and on which equipment. Production scheduling aims to maximize the efficiency of the operation and reduce costs..

Search algorithms/strategies¶

The values for variables come out of an enumeration process. ‘Intelligent’ enumeration strategies adapted to special types of constraints and variables are a central issue in CP. The search is controlled by problem specific heuristics, strategies from Mathematical Programming or the expert’s knowledge; fixing variables to trial values is possible. One can distinguish variable and value selection heuristics. Due to the way the backtracking mechanism works, usually depth-first search is used.

Session¶

The structure which is in charge of managing one or several problems in Artelys Kalis.

Solution¶

A set of values that can be assigned to the variables of the problem and which verify all constraints.

Solution methods¶

Finite domain CP problems are usually solved by tree search methods (Branch-and-Bound for optimization, Branch-and-Prune for decision problems) that enumerate the possible values of the variables coupled with consistency algorithms. In tree search methods with consistency checking the local consistency algorithm is triggered by the propagation of the domain changes of the branching variable. For optimization usually a cost constraint is introduced that propagates to the variables. It is updated (in the case of minimization: bounded to be smaller than the solution value) each time a new solution is found.

Solver¶

The object in charge of the search process. It can look for one or many solutions but can also optimize a problem. It manages the tree search and its behavior can be modified thanks to user-defined strategies.

System of constraints¶

A conjunctive set of constraints, usually built up incrementally.

Tree search¶

An algorithm looking for solutions and constructing a set of nodes. The first one represents the original problem. It can be divided in different parts thanks to variable fixing or cuts adding and gives like that sub-problems which are physically sub-nodes in a tree keeping all nodes made during search.

Variable¶

Object that has a name and a domain (also referred to as decision variable).