Paint production 2¶

In this section we work once more with the paint production problem. The objective of this problem is to determine a production cycle of minimal length for a given set of jobs with sequence-dependent cleaning times between every pair of jobs.

Model formulation¶

The problem formulation in section 11.5 uses KAllDifferent constraints to ensure that every job occurs once only, calculates the duration of cleaning times with KElement constraints, and introduces auxiliary variables and constraints to prevent subcycles in the production sequence. All these constraints can be expressed by a single constraint relation, the KCycle constraint. 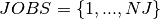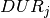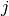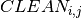Let $JOBS = \{1, ..., NJ\}$ be the set of batches to produce, $DUR_j$ the processing time for batch $j$ , and $CLEAN_{i,j}$ the cleaning time between the consecutive batches 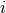$i$ and $j$ . 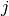As before we define decision variables 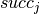$succ_j$ taking their values in $JOBS$ , to indicate the successor of every job. The complete model formulation is the following,

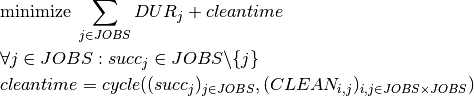
$&\text{minimize } \sum_{j \in JOBS} DUR_j + cleantime\\ &\forall j \in JOBS : succ_j \in JOBS \backslash \{ j \}\\ &cleantime = cycle((succ_j)_{j \in JOBS}, (CLEAN_{i,j})_{i,j \in JOBS \times JOBS})\\$

where cycle stands for the relation sequence into a single cycle without subcycles or repetitions. The variable cleantime equals the total duration of the cycle.

Implementation¶

The model using the KCycle constraint looks as follows.

// Number of paint batches (=jobs)
int NJ = 5;
// Durations of jobs
int DUR[]  = {40, 35, 45 ,32 ,50};

// Cleaning times between jobs
KIntMatrix CLEAN(5,5,0,"CLEAN");

CLEAN[0][0] = 0;CLEAN[1][0] = 11;CLEAN[2][0] = 7;CLEAN[3][0] = 13;CLEAN[4][0] = 11;
CLEAN[0][1] = 5;CLEAN[1][1] = 0;CLEAN[2][1] = 13;CLEAN[3][1] = 15;CLEAN[4][1] = 15;
CLEAN[0][2] = 13;CLEAN[1][2] = 15;CLEAN[2][2] = 0;CLEAN[3][2] = 23;CLEAN[4][2] = 11;
CLEAN[0][3] = 9;CLEAN[1][3] = 13;CLEAN[2][3] = 5;CLEAN[3][3] = 0;CLEAN[4][3] = 3;
CLEAN[0][4] = 3;CLEAN[1][4] = 7;CLEAN[2][4] = 7;CLEAN[3][4] = 7;CLEAN[4][4] = 0;

// Cleaning times after a batch
KIntArray CB;

// Successor of a batch
KIntVarArray succ;
// Objective variable
KIntVar * cycleTime;
// Objective variable
KIntVar * cleanTime;


// Creation of the problem in this session
KProblem problem(session,"B-5 Paint production");

// variables creation
char name[80];
int j,i;
for (j=0;j<NJ;j++) {
    sprintf(name,"succ(%i)",j);
    succ += (* new KIntVar( problem,name,0,NJ-1) );
    succ[j].remVal(j);
}

cleanTime = new KIntVar(problem,"cleanTime",0,1000);
// Assign values to 'succ' variables as to obtain a single cycle
// 'cleanTime' is the sum of the cleaning times
problem.post(new KCycle(&succ, NULL,cleanTime, &CLEAN) );

// objective variable creation
cycleTime = new KIntVar(problem,"cycleTime",0,1000);

// Objective: minimize the duration of a production cycle
KLinTerm cycleTerm;
for (j=0;j<NJ;j++) {
    cycleTerm = cycleTerm + DUR[j];
}
problem.post(cycleTerm + *cleanTime == *cycleTime);

// propagating problem
if (problem.propagate()) {
    printf("Problem is infeasible\n");
    exit(1);
}

// Solve the problem
// creation of the solver
KSolver solver(problem);

// setting objective and sense of optimization
problem.setSense(KProblem::Minimize);
problem.setObjective(*cycleTime);

int result = solver.optimize();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();

// Solution printing
printf("Minimum cycle time: %i\n", sol->getValue(*cycleTime));
printf("Sequence of batches:\nBatch Duration Cleaning\n");
int first=0;
do {
    printf("%i\t%i\t%i\n", first, DUR[first],CLEAN[first][sol->getValue(succ[first])]);
    first = sol->getValue(succ[first]);
} while (first!=0);

from kalis import *

### Data
# Number of paint batches (=jobs)
nb_jobs = 5
# Durations of jobs
jobs_durations  = [40, 35, 45, 32, 50]

# Cleaning times between jobs
jobs_cleaning_times = [[0, 11, 7, 13, 11],
            [5, 0, 13, 15, 15],
            [13, 15, 0, 23, 11],
            [9, 13, 5, 0, 3],
            [3, 7, 7, 7, 0]]

### Creation of the problem
# Creation of the Kalis session
session = KSession()
# Creation of the problem in this session
problem = KProblem(session, "B-5 Paint production")

# Setting data as a KIntMatrix
K_cleaning_times_matrix = KIntMatrix(5, 5, 0, "CLEAN")
for i in range(nb_jobs):
    for j in range(nb_jobs):
        K_cleaning_times_matrix.setMatrix(i, j, jobs_cleaning_times[i][j])

### Variables creation
# Successor of a batch
batch_successor = KIntVarArray()
for j in range(nb_jobs):
    batch_successor += KIntVar(problem, "succ(%d)" % j, 0, nb_jobs - 1)
    batch_successor[j].remVal(j)
# Cycle time monitoring
clean_time = KIntVar(problem, "cleanTime", 0, 1000)

# Assign values to 'batch_successor' variables as to obtain a single cycle
# 'clean_time' is the sum of the cleaning times
problem.post(KCycle(batch_successor, None, clean_time, K_cleaning_times_matrix))

# Objective variable
cycle_time = KIntVar(problem, "cycleTime", 0, 1000)
problem.post(sum(jobs_durations) + clean_time == cycle_time)

### Solve the problem
# First propagation to check inconsistency
if problem.propagate():
    print("Problem is infeasible")
    sys.exit(1)

# Set the solver
solver = KSolver(problem)

# Setting objective and sense of optimization
problem.setSense(KProblem.Minimize)
problem.setObjective(cycle_time)

# Run optimization
result = solver.optimize()
# Solution printing
if result:
    solution = problem.getSolution()
    solution.printResume()
    print("Minimum cycle time: %d" % solution.getValue(cycle_time))
    print("Sequence of batches:")
    print("Batch Duration Cleaning")
    j = solution.getValue(batch_successor[0])
    while j != 0:
        next_job = solution.getValue(batch_successor[j])
        print("%d\t%d\t%d" % (j, jobs_durations[j], jobs_cleaning_times[j][next_job]))
        j = next_job

 // Cleaning times between jobs
 KIntMatrix CLEAN = new KIntMatrix(5,5,0,"CLEAN");

 CLEAN.setMatrix(0,0,0);
 CLEAN.setMatrix(1,0,11);
 CLEAN.setMatrix(2,0,7);
 CLEAN.setMatrix(3,0,13);
 CLEAN.setMatrix(4,0,11);
 CLEAN.setMatrix(0,1,5);
 CLEAN.setMatrix(1,1,0);
 CLEAN.setMatrix(2,1,13);
 CLEAN.setMatrix(3,1,15);
 CLEAN.setMatrix(4,1,15);
 CLEAN.setMatrix(0,2,13);
 CLEAN.setMatrix(1,2,15);
 CLEAN.setMatrix(2,2,0);
 CLEAN.setMatrix(3,2,23);
 CLEAN.setMatrix(4,2,11);
 CLEAN.setMatrix(0,3,9);
 CLEAN.setMatrix(1,3,13);
 CLEAN.setMatrix(2,3,5);
 CLEAN.setMatrix(3,3,0);
 CLEAN.setMatrix(4,3,3);
 CLEAN.setMatrix(0,4,3);
 CLEAN.setMatrix(1,4,7);
 CLEAN.setMatrix(2,4,7);
 CLEAN.setMatrix(3,4,7);
 CLEAN.setMatrix(4,4,0);

// Successor of a batch
 KIntVarArray succ = new KIntVarArray();
 // Objective variable
 KIntVar cycleTime = new KIntVar();
 // Objective variable
 KIntVar cleanTime = new KIntVar();

 // Creation of the problem in this session
 KProblem problem = new KProblem(session,"B-5 Paint production");

 // variables creation
 int j;
 for (j=0; j<NJ; j++)
 {
     succ.add(new KIntVar(problem, "succ(" + j + ")",0, NJ-1) );
     succ.getElt(j).remVal(j);
 }

 cleanTime = new KIntVar(problem, "cleanTime", 0, 1000);
 // Assign values to 'succ' variables as to obtain a single cycle
 // 'cleanTime' is the sum of the cleaning times
 problem.post(new KCycle(succ, null,cleanTime, CLEAN) );

 // objective variable creation
 cycleTime = new KIntVar(problem, "cycleTime", 0, 1000);

 // Objective: minimize the duration of a production cycle
 int sumOfDUR = 0;
 for (j=0; j<NJ; j++)
 {
     sumOfDUR += DUR[j];
 }

 problem.post(new KGreaterOrEqualXyc(cycleTime, cleanTime, sumOfDUR));

 // propagating problem
 if (problem.propagate())
 {
     System.out.println("Problem is infeasible");
     exit(1);
 }

 // Solve the problem
 // creation of the solver
 KSolver solver = new KSolver(problem);

 // setting objective and sense of optimization
 problem.setSense(KProblem.Sense.Minimize);
 problem.setObjective(cycleTime);

 solver.optimize();
 // solution printing
 KSolution sol = problem.getSolution();
 // print solution resume
 sol.printResume();

 // Solution printing
 System.out.println("Minimum cycle time: " + sol.getValue(cycleTime));
 System.out.print("Sequence of batches:\nBatch Duration Cleaning\n");
 int first=0;
 do {
     System.out.print(first + "\t" + DUR[first] + "\t" + intp_value(CLEAN.getMatrix(first,sol.getValue(succ.getElt(first)))) + "\n");
     first = sol.getValue(succ.getElt(first));
 } while (first!=0);

Results¶

The optimal solution to this problem has a minimum cycle time of 243 minutes, resulting from 202 minutes of (incompressible) processing time and 41 minutes of cleaning. The problem statistics produced by Artelys Kalis for a model run reveal that the cycle version of this model is the most efficient way of representing and solving the problem: it takes fewer nodes and a shorter execution time than the two previous versions of the model.