Multi-Mode Resource Constrained Project Scheduling Problem (MRCPSP)¶

The Resource Constrained Project Scheduling Problem (RCPSP) consists in determining the start time of each task of a project, these tasks being subject to precedence and resources constraints. The precedence constraints are defined by the impossibility to start processing a task while the processing of at least one of its predecessor is not finished. Each task consumes a certain amount of resources, all of which are renewable. This means that all the consumptions of tasks are restored to the resource once the task’s processing is finished. In the RCPSP, the tasks’ duration is fixed. For the Multi-Mode version (MRCPSP), both the duration and the consumptions of tasks depend on the mode assigned to the task.

Model formulation¶

To express a mathematical model for the MRCPSP suited for Artelys Kalis, we will use Tasks, which are objects that rely on integer variables as their start time, duration time and end time. We note 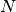$N$ the number of tasks to schedule and for each task 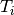$T_i$ its start time is an integer variable 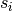$s_i$ , its duration is an integer variable 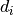$d_i$ and its end time is an integer variable $e_i$ .

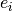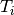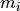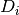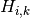As said, the MRCPSP is different from the RCPSP by the fact that the durations and resource consumptions of tasks depend on their mode. For a task $T_i$ , its mode is an integer variable $m_i$ , the set of potential durations $D_i$ and $H_{i,k}$ is the set of potential consumption on each resource 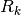$R_k$ . For each task 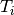$T_i$ and each resource 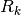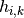$R_k$ , $h_{i,k}$ is an integer variable representing the consumption of task 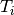$T_i$ on resource $R_k$ .

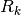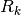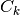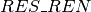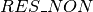For each resource $R_k$ , its capacity (or availability) is noted $C_k$ , and the number of renewable resources is noted $RES\_REN$ , while the number of non-renewable resources is noted $RES\_NON$ .

Finally, we note 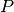$P$ the set of precedence, with 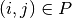$(i,j) \in P$ meaning that task 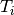$T_i$ precedes task $T_j$ .

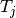We therefore have the following model for the MRCPSP:

$&\forall (i,j) \in P, e_i \leq s_j\\ &\forall i \in \{1, \dots, N\}, s_i + d_i = e_i\\ &\forall k \in \{1, \dots, RES\_REN\}, \text{cumulative}(\{T_1, \dots, T_N \}, \{h_{1,k}, \dots, h_{N,k} \}, C_k)\\ &\forall k \in \{1, \dots, RES\_NON\}, \sum\limits_{i = 1}^{N} h_{i,k} \leq C_{k}\\ &\forall i \in \{1, \dots, N\}, d_i = D_i[ \,m_i] \,\\ &\forall i \in \{1, \dots, N\}, \forall k \in \{1, \dots, RES\}, h_{i,k} = H_{i,k}[ \,m_i] \,\\$

Let note that the last two sets of constraints of our model are implemented using element constraints.

Implementation¶

In this section, we will see how to implement the mathematical model formulated above using the different interfaces of Artelys Kalis. Most especially, we will benefit from the API dedicated to scheduling problems.

#include <iostream>
        #include <sstream>

        // Including "kalis.h" to access the library
        #include "Kalis.h"

        // ********************************************************************
        // * Main Program                                                     *
        // ********************************************************************

        int min(int a[], int size) {
                int min = a[0];
                for(int i = 1; i < size; i++) {
                        if(min > a[i]) {
                                min = a[i];
                        }
                }
                return min;
        }

        int max(int a[], int size) {
                int max = a[0];
                for(int i = 1; i < size; i++) {
                        if(max < a[i]) {
                                max = a[i];
                        }
                }
                return max;
        }

        template <size_t x, size_t y, size_t z>
        int * retrieveConsumptions(int nbModes[], int (&consumptions)[x][y][z], int task, int res) {
                int *c = new int[nbModes[task]];
                for(int i = 0; i < nbModes[task]; i++) {
                        c[i] = consumptions[task][i][res];
                }
                return c;
        }

        int main(void) {
                // *** Description of datas

                // *** Number of tasks in the project
                int const nbTasks = 10;

                // *** Number of resources
                int const nbResources = 4;

                // *** Number of renewable resources
                int const nbResRen = 2;

                // *** Horizon
                int const horizon = 61;

                // *** Number of modes of each task
                int nbModes[10] = {3, 3, 3, 3, 1, 3, 3, 3, 3, 3};

                // *** Set of successors of eack task
                int nbSuccessors[10] = {2, 2, 1, 2, 2, 2, 1, 1, 0, 0};
                int successors[][nbTasks] = {
                        {2, 3},
                        {3, 4},
                        {5},
                        {5, 6},
                        {6, 7},
                        {8, 9},
                        {9},
                        {9},
                        {},
                        {}
                };

                // *** Duration of eack task depending on their mode
                int durations[nbTasks][3] = {
                        {3, 5, 7},
                        {1, 4, 8},
                        {2, 3, 4},
                        {4, 5, 5},
                        {3},
                        {2, 4, 8},
                        {4, 5, 9},
                        {2, 3, 5},
                        {2, 4, 5},
                        {1, 4, 7}
                };

                // *** Consumption of resources by tasks depending on their mode: consumptions[idTask][idMode][idResource]
                int consumptions[nbTasks][3][nbResources] = {
                        {{4, 2, 4, 5}, {2, 2, 3, 4}, {2, 1, 2, 1}},
                        {{5, 4, 4, 5}, {3, 3, 0, 3}, {2, 2, 0, 0}},
                        {{3, 3, 2, 0}, {2, 3, 2, 0}, {2, 2, 1, 0}},
                        {{3, 3, 4, 5}, {3, 3, 2, 0}, {3, 3, 0, 2}},
                        {{5, 5, 0, 0}},
                        {{4, 4, 4, 7}, {3, 3, 2, 5}, {2, 2, 0, 4}},
                        {{3, 2, 7, 3}, {3, 2, 3, 5}, {3, 2, 0, 0}},
                        {{2, 2, 5, 6}, {2, 4, 3, 3}, {2, 2, 0, 1}},
                        {{3, 3, 6, 4}, {4, 3, 4, 4}, {2, 2, 2, 2}},
                        {{4, 4, 6, 9}, {3, 3, 3, 5}, {4, 3, 2, 4}}
                };

                // *** Resource capacities
                int resourceAvailabilities[nbResources] = {8, 7, 20, 25};

                try {

                        // *** Creation of the Session
                        KSession session;

                        // *** Modeling of the problem
                        // *** Creation of the problem "MRCPSP" in this Session
                        KProblem problem(session, const_cast<char *>("MRCPSP"));

                        // Creation of the schedule
                        KSchedule schedule(problem, "Schedule", 0, horizon);

                        // Create tasks
                        KTask *tasks = new KTask[nbTasks];
                        for(int i = 0; i < nbTasks; i++) {
                                std::stringstream sout("");
                                sout << "task(" << i << ")";
                                tasks[i] = KTask(schedule, sout.str().c_str(), 0, horizon, min(durations[i], nbModes[i]), max(durations[i], nbModes[i]));
                        }

                        // Precedence
                        for(int i = 0; i < nbTasks; i++) {
                                for(int j = 0; j < nbSuccessors[i]; j++) {
                                        tasks[successors[i][j]].startsAfter(tasks[i]);
                                }
                        }

                        // Resources
                        KIntVar *resourceConsumptions = new KIntVar[nbTasks*nbResources];
                        // renewable resources
                        KResource *resources = new KResource[nbResources];
                        for(int j = 0; j < nbResources; j++) {
                                std::stringstream sout("");
                                sout << "res(" << j << ")";
                                resources[j] = KDiscreteResource(schedule, sout.str().c_str(), resourceAvailabilities[j]);
                                for(int i = 0; i < nbTasks; i++) {
                                        int *c = retrieveConsumptions(nbModes, consumptions, i, j);
                                        if(j < nbResRen) {
                                                tasks[i].requires(resources[j], min(c, nbModes[i]), max(c, nbModes[i]));
                                                resourceConsumptions[i*nbResources + j] = * tasks[i].getRequiresVar(&resources[j]);
                                        } else {
                                                tasks[i].consumes(resources[j], min(c, nbModes[i]), max(c, nbModes[i]));
                                                resourceConsumptions[i*nbResources + j] = * tasks[i].getConsumesVar(&resources[j]);
                                        }
                                        delete [] c;
                                }
                        }

                        // Manage modes
                        KIntVarArray modes;
                        for(int i = 0; i < nbTasks; i++) {
                                std::stringstream sout("");
                                sout << "mode(" << i << ")";
                                modes += KIntVar(problem, sout.str().c_str(), 0, nbModes[i] - 1);

                                KIntArray durationsValues;
                                for(int k = 0; k < nbModes[i]; k++) {
                                        durationsValues += durations[i][k];
                                }
                                KEltTerm kelt(durationsValues, *(modes.getElt(i)));
                                problem.post(new KElement(kelt, *(tasks[i].getDurationVar())));
                                for(int j = 0; j < nbResources; j++) {
                                        KIntArray consumptionsValues;
                                        for(int k = 0; k < nbModes[i]; k++) {
                                                consumptionsValues += consumptions[i][k][j];
                                        }
                                        KEltTerm keltConsumptions(consumptionsValues, *(modes.getElt(i)));
                                        problem.post(new KElement(keltConsumptions, resourceConsumptions[i*nbResources + j]));
                                }
                        }

                        schedule.close();

                        KBranchingSchemeArray myBranchingSchemeArray;
                        KIntVarArray intvarArray;
                        for(int i = 0; i < nbTasks; i++) {
                                intvarArray += *(tasks[i].getStartDateVar());
                                intvarArray += *(modes.getElt(i));
                        }
                        myBranchingSchemeArray += KAssignVar(KInputOrder(),KMinToMax(), intvarArray);

                        // problem.print();

                        // propagating problem
                        if (problem.propagate()) {
                                std::cout << "Problem is infeasible" << std::endl;
                                exit(1);
                        }

                        // *** Creation of the solver using our tree search controls for this problem
                        KSolver solver(problem, myBranchingSchemeArray);

                        solver.optimize();

                        // *** Get the last ( therefore the best ) solution and store it in a Solution object
                        KSolution solution = problem.getSolution();

                        // *** Print variables values for this solution
                        std::cout << "Best solution :" << std::endl;
                        solution.print();

                        // *** Print the objective value
                        std::cout << "Objective Value = " << solution.getObjectiveValue() << std::endl;

                        delete [] tasks;
                        delete [] resourceConsumptions;
                        delete [] resources;

                } catch (ArtelysException &artelysException) {
                        // *** An error occured
                        std::cout << "Exception " << artelysException.getCode() << " raised : " << artelysException.getMessage() << std::endl;
                }

                return 0;
        }

from kalis import *


### Data
nb_activities = 10
nb_resources = 4
nb_resources_renewable = 2
nb_resources_non = 2
horizon = 61

nb_modes = [3, 3, 3, 3, 1, 3, 3, 3, 3, 3]
successors = [[2, 3],
              [3, 4],
              [5],
              [5, 6],
              [6, 7],
              [8, 9],
              [9],
              [9],
              [],
              []
              ]

durations_by_modes = [[3, 5, 7],
                      [1, 4, 8],
                      [2, 3, 4],
                      [4, 5, 5],
                      [3],
                      [2, 4, 8],
                      [4, 5, 9],
                      [2, 3, 5],
                      [2, 4, 5],
                      [1, 4, 7]
                      ]

resources_usages = [[[4, 2, 4, 5], [2, 2, 3, 4], [2, 1, 2, 1]],
                    [[5, 4, 4, 5], [3, 3, 0, 3], [2, 2, 0, 0]],
                    [[3, 3, 2, 0], [2, 3, 2, 0], [2, 2, 1, 0]],
                    [[3, 3, 4, 5], [3, 3, 2, 0], [3, 3, 0, 2]],
                    [[5, 5, 0, 0]],
                    [[4, 4, 4, 7], [3, 3, 2, 5], [2, 2, 0, 4]],
                    [[3, 2, 7, 3], [3, 2, 3, 5], [3, 2, 0, 0]],
                    [[2, 2, 5, 6], [2, 4, 3, 3], [2, 2, 0, 1]],
                    [[3, 3, 6, 4], [4, 3, 4, 4], [2, 2, 2, 2]],
                    [[4, 4, 6, 9], [3, 3, 3, 5], [4, 3, 2, 4]]
                    ]

resources_availabilities = [8, 7, 20, 25]


def get_consumption_domain_modes(activity, res):
    consumption_domain_modes = []
    for i_mode in range(nb_modes[activity]):
        consumption_domain_modes.append(resources_usages[activity][i_mode][res])
    return consumption_domain_modes


### Model
tasks = {}
modes = {}
resources = {}
consumptions = {}
session = KSession()
problem = KProblem(session, "PSP problem")
schedule = KSchedule(problem, "PSP schedule", 0, horizon)
### Variables creation
# Tasks to be planned
for act in range(nb_activities):
    d = durations_by_modes[act]
    tasks[act] = KTask(schedule, "task(" + str(act) + ")", 0, horizon, min(d), max(d))
    consumptions[act] = dict()
# Declare resources
for j in range(nb_resources):
    resources[j] = KDiscreteResource(schedule, "res(" + str(j) + ")",
                                    resources_availabilities[j],
                                    KDiscreteResource.TimeTabling)
# Declare consumption variables
for act in range(nb_activities):
    for j in range(nb_resources):
        c = get_consumption_domain_modes(act, j)
        if j < nb_resources_renewable:
            tasks[act].requires(resources[j], min(c), max(c))
            consumptions[act][j] = tasks[act].getRequiresVar(resources[j])
        else:
            tasks[act].consumes(resources[j], min(c), max(c))
            consumptions[act][j] = tasks[act].getConsumesVar(resources[j])

### Constraints
# Setting the successors of each task
for i1 in range(nb_activities):
    for i2 in successors[i1]:
        tasks[i2].startsAfter(tasks[i1])

for act in range(nb_activities):
                modes[act] = KIntVar(problem, "mode(" + str(act) + ")", 0, nb_modes[act] - 1)
                # Durations of tasks depend of their mode
    durations = KIntArray()
    for im in range(nb_modes[act]):
        durations.add(durations_by_modes[act][im])
    problem.post(KElement(durations, modes[act], tasks[act].getDurationVar()))
                # Tasks' consumption on resources depend of their mode
                for act in range(nb_activities):
                        for j in range(nb_resources):
                                consumption_by_modes = KIntArray()
                                for im in range(nb_modes[act]):
                                        consumption_by_modes.add(resources_usages[act][im][j])
                                problem.post(KElement(consumption_by_modes, modes[act], consumptions[act][j]))

schedule.close()

        myBranchingSchemeArray = KBranchingSchemeArray()
        intvarArray = KIntVarArray()
        for i in range(nb_activities):
                intvarArray += tasks[i].getStartDateVar()
                intvarArray += modes.get(i)
        myBranchingSchemeArray += KAssignVar(KInputOrder(), KMinToMax(), intvarArray)

### Solve the problem
# First propagation to check inconsistency
if problem.propagate():
    print("Problem is infeasible")
    sys.exit(1)

# Set the solver
solver = KSolver(problem, myBranchingSchemeArray)

# Run optimization
result = solver.optimize()
# Solution printing
if result:
    solution = problem.getSolution()
    solution.printResume()
    makespan_value = solution.getValue(schedule.getObjective())
    print("makespan_value=", makespan_value)

import com.artelys.kalis.*;

import java.util.stream.IntStream;

public class MRCPSP {
    public static final int NB_ACTIVITIES = 10;
    public static final int NB_RESOURCES = 4;
    public static final int RES_REN = 2;
    public static final int HORIZON = 61;

    public static final int[] NB_MODES = new int[]{
            3, 3, 3, 3, 1, 3, 3, 3, 3, 3
    };

    public static final int[][] SUCCESSORS = new int[][]{
            {2, 3},
            {3, 4},
            {5},
            {5, 6},
            {6, 7},
            {8, 9},
            {9},
            {9},
            {},
            {}
    };

    public static final int[][] DURATIONS = new int[][]{
            {3, 5, 7},
            {1, 4, 8},
            {2, 3, 4},
            {4, 5, 5},
            {3},
            {2, 4, 8},
            {4, 5, 9},
            {2, 3, 5},
            {2, 4, 5},
            {1, 4, 7}
    };

    public static final int[][][] CONSUMPTIONS = new int[][][] {
            {{4, 2, 4, 5}, {2, 2, 3, 4}, {2, 1, 2, 1}},
            {{5, 4, 4, 5}, {3, 3, 0, 3}, {2, 2, 0, 0}},
            {{3, 3, 2, 0}, {2, 3, 2, 0}, {2, 2, 1, 0}},
            {{3, 3, 4, 5}, {3, 3, 2, 0}, {3, 3, 0, 2}},
            {{5, 5, 0, 0}},
            {{4, 4, 4, 7}, {3, 3, 2, 5}, {2, 2, 0, 4}},
            {{3, 2, 7, 3}, {3, 2, 3, 5}, {3, 2, 0, 0}},
            {{2, 2, 5, 6}, {2, 4, 3, 3}, {2, 2, 0, 1}},
            {{3, 3, 6, 4}, {4, 3, 4, 4}, {2, 2, 2, 2}},
            {{4, 4, 6, 9}, {3, 3, 3, 5}, {4, 3, 2, 4}}
    };

    public static final int[] RESOURCE_AVAILABILITIES = new int[]{
            8, 7, 20, 25
    };

    public static int[] retrieveConsumptions(int activity, int res) {
        return IntStream.range(0, NB_MODES[activity]).map(k -> CONSUMPTIONS[activity][k][res]).toArray();
    }

    public static int min(int[] a) {
        int min = a[0];
        for(int i = 1; i < a.length; i++) {
            if(min > a[i]) {
                min = a[i];
            }
        }
        return min;
    }

    public static int max(int[] a) {
        int max = a[0];
        for(int i = 1; i < a.length; i++) {
            if(max < a[i]) {
                max = a[i];
            }
        }
        return max;
    }

    public static void main(String[] args) {
        try {
            System.loadLibrary("Kalis");        // uses java option -Djava.library.path=path to find Kalis.dll
            System.loadLibrary("KalisJava");    // uses java option -Djava.library.path=path to find KalisJava.dll

            // Creation of the session
            KSession session = new KSession();
            // Creation of the problem
            KProblem problem = new KProblem(session,"RCPSP multi-mode");

            // Creation of the schedule
            KSchedule schedule = new KSchedule(problem, "Schedule", 0, HORIZON);

            // Create tasks
            KTask[] tasks = new KTask[NB_ACTIVITIES];
            for(int i = 0; i < NB_ACTIVITIES; i++) {
                int[] d = DURATIONS[i];
                tasks[i] = new KTask(schedule, "task(" + i + ")", 0, HORIZON, min(d), max(d));
            }

            // Precedence
            for(int i = 0; i < NB_ACTIVITIES; i++) {
                for(int j = 0; j < SUCCESSORS[i].length; j++) {
                    tasks[SUCCESSORS[i][j]].startsAfter(tasks[i]);
                }
            }

            // Resources
            KIntVar[][] resourceConsumptions = new KIntVar[NB_ACTIVITIES][NB_RESOURCES];
            // renewable resources
            KDiscreteResource[] resources = new KDiscreteResource[NB_RESOURCES];
            for(int j = 0; j < resources.length; j++) {
                resources[j] = new KDiscreteResource(schedule, "res(" + j + ")", RESOURCE_AVAILABILITIES[j]);
                for(int i = 0; i < NB_ACTIVITIES; i++) {
                    int[] c = retrieveConsumptions(i, j);
                    if(j < RES_REN) {
                        tasks[i].requires(resources[j], min(c), max(c));
                        resourceConsumptions[i][j] = tasks[i].getRequiresVar(resources[j]);
                    } else {
                        tasks[i].consumes(resources[j], min(c), max(c));
                        resourceConsumptions[i][j] = tasks[i].getConsumesVar(resources[j]);
                    }
                }
            }

            // Manage modes
            KIntVarArray modes = new KIntVarArray();
            for(int i = 0; i < NB_ACTIVITIES; i++) {
                modes.add(new KIntVar(problem, "mode(" + i + ")", 0, NB_MODES[i] - 1));

                KIntArray durations = new KIntArray();
                for(int k = 0; k < NB_MODES[i]; k++) {
                    durations.add(DURATIONS[i][k]);
                }
                problem.post(new KElement(durations, modes.getElt(i), tasks[i].getDurationVar(), 0));
                for(int j = 0; j < NB_RESOURCES; j++) {
                    KIntArray consumptions = new KIntArray();
                    for(int k = 0; k < NB_MODES[i]; k++) {
                        consumptions.add(CONSUMPTIONS[i][k][j]);
                    }
                    problem.post(new KElement(consumptions, modes.getElt(i), resourceConsumptions[i][j], 0));
                }
            }

            schedule.close();

                                KBranchingSchemeArray myBranchingSchemeArray = new KBranchingSchemeArray();
                                KIntVarArray intvarArray = new KIntVarArray();
                                for(int i = 0; i < tasks.length; i++) {
                                        intvarArray.add(tasks[i].getStartDateVar());
                                        intvarArray.add(modes.getElt(i));
                                }
                                myBranchingSchemeArray.add(new KAssignVar(new KInputOrder(), new KMinToMax(), intvarArray));

            // Propagating the constraints
            if (problem.propagate()) {
                System.out.println("Problem is infeasible");
                System.exit(1);
            }

            // Minimize the makespan
            KSolver solver = new KSolver(problem, myBranchingSchemeArray);
                                int result = solver.optimize();
            if (result == 0) {
                System.out.println("No solution found");
                System.exit(1);
            }

            // Printing solution
            problem.getSolution().print();
            double makespanValue = problem.getSolution().getValue(schedule.getObjective());
            System.out.println("makespan_value= "+makespanValue);
        } catch(Exception e) {
            e.printStackTrace();
        }
    }
}

Results¶

The minimum makespan of the schedule is 20, with the following start times and modes for the tasks:

Task	0	1	2	3	4	5	6	7	8	9
Start Time	0	0	7	7	4	12	12	9	16	16
Mode	2	1	0	2	0	1	0	2	1	1