Solving a constraint problem¶
In this chapter, you will:
be introduced to the main classes of Artelys Kalis;
learn how to apply these to the formulation of constraint problems;
learn how to solve such problems and explore their solutions.
A simple personal planning example¶
This problem will be used as example throughout this chapter. We will show how Artelys Kalis can be used to state and solve this problem, introducing main concepts and classes.
Let suppose that a movie theatre director has to decide in which location each of his employees should be posted. There are eight employees, named Andrew, David, Jane, Jason, Leslie, Michael, Marilyn and Oliver. There are four locations: the ticket office, the first entrance, the second entrance and the cloakroom. These locations require 3, 2, 2, and 1 person respectively.
The variables of the problem are the locations where each employee will work.
There are some constraints associated with this problem:
each employee must have a unique location;
Leslie must work at the second entrance;
Michael must work at the first entrance;
David, Michael and Jason cannot work together;
each location must be occupied by exactly the number of employees it requires;
if David is selling tickets, Marilyn must be with him.
Solving the problem means finding values of the variables satisfying all the constraints.
In the following sections of this chapter, we show how this problem can be solved using Artelys Kalis library in a C++ program. This program is described in a step-by-step manner, allowing you to become familiar with the main classes of the library.
The KSession class¶
Nothing can be done in Artelys Kalis outside a KSession object. All the stated and solved must problems be held by such an object : for this reason the creation of a KSession object is the first thing to do at the beginning of the program.
The KSession class has one principal functionality:
license checking: when created, the
KSessionobject will look for a valid license of the software.
The syntax for the creation of a KSession object is the following:
try
{
KSession mySession;
}
catch (ArtelysException &artelysException)
{
cout << artelysException.getMessage() << endl;
}
try:
session = KSession()
except ArtelysException as e:
print(e)
try {
KSession session = new KSession();
} catch (Exception e) {
e.printStackTrace();
}
This statement creates a KSession object variable named mySession. The library will print to the standard output a banner showing the version of the library and a copyrights notice.
We could have created our KSession using this syntax:
try
{
KSession mySession(false);
}
catch (ArtelysException &artelysException)
{
cout << artelysException.getMessage();
}
try:
session = KSession(False)
except ArtelysException as e:
print(e)
try {
KSession session = new KSession(false);
} catch (Exception e) {
e.printStackTrace();
}
In this case, the banner will not be printed to the standard output.
Warning
Only one KSession object can be used in a program. An exception will be raised if you try to have two sessions in memory at the same time.
Creating the problem¶
Our personnel planning example comprises variables, constraints (modeling entities) and might have solutions after search. Such problems are represented in Artelys Kalis by objets of the class KProblem. These objects are holding the modeling entities objects, the solutions objects and (when optimizing, see Chapter 5) the objective variable object and the sense of the optimization.
Here is how we can declare and create the KProblem which will hold all the information for solving our planning example:
KProblem problem(session,"Movie Theater");
problem = KProblem(session, "Movie Theater")
KProblem problem = new KProblem(session,"Movie Theater");
This statement creates a KProblem object variable named problem hold by the KSession object session. “Movie Theater” is the internal name of the problem.
Note that a KSession can hold any number of problems: this number is only limited by the hardware memory of the computer.
Adding decision variables to the problem¶
Decision variables are the variable quantities that we are trying to instantiate in order to satisfy the constraints of our problem. Artelys Kalis can works with integer variables: decision variables which are constrained to take only integer values. These integer variables are represented by instances of the class KIntVar.
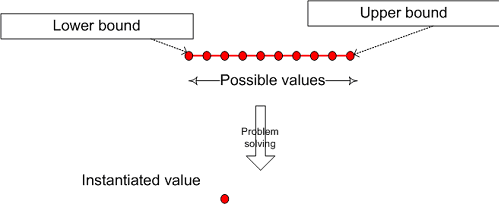
Fig. 2 Illustration of decision variables in Kalis¶
KIntVar objects can be gathered to KIntVarArray: this class represents ordered sets of integer variables sharing a common property, in a large sense. This could be: all these variables are present in the same constraint, all these variables represent locations, etc. The only requirement on these variables is that they all must be owned by the same problem. In our example, we put all our decision variables (each one representing the location of an employee) in such a set. The syntax to be used in order to declare this set is:
KIntVarArray dutyOf;
dutyOf = KIntVarArray()
KIntVarArray dutyOf = new KIntVarArray();
This statement creates a KIntVarArray object variable named dutyOf. The nth variable in dutyOf will be the location where the nth employee is assigned. The locations are
represented by integer values, between 0 (ticket office) and 3 (cloakroom). We can declare, create and add these variables to dutyOf in a very concise manner:
int nbPersons = 8;
char peopleNames[8][20] = {"David", "Andrew", "Leslie", "Jason", "Oliver", "Michael", "Jane", "Marylin"};
int nbDuties = 4;
for(int indexPerson = 0; indexPerson < nbPersons; indexPerson++)
{
dutyOf += KIntVar(problem,peopleNames[indexPerson],0,nbDuties-1);
}
nbPersons = 8
peopleNames = ["David", "Andrew", "Leslie", "Jason", "Oliver", "Michael", "Jane", "Marylin"]
nbDuties = 4
for indexPerson in range(nbPersons):
dutyOf += KIntVar(problem,peopleNames[indexPerson],0,nbDuties-1)
int nbPersons = 8;
String[] peopleNames = {"David", "Andrew", "Leslie", "Jason", "Oliver", "Michael", "Jane", "Marylin"};
int nbDuties = 4;
for(int indexPerson = 0; indexPerson < nbPersons; indexPerson++)
{
dutyOf.add(new KIntVar(problem,peopleNames[indexPerson],0,nbDuties-1));
}
In the C++ for loop, for each employee between 0 (David) and 7 (Marilyn), we:
declare and create a
KIntVarobject variable, added toproblem, whose internal name is the name of the employee (stored in thepeopleNamesC++ char array) and which can be instantiated to values between 0 and 3: the interval [0,3] is the domain of this variable;push this variable into
dutyOf, at the last place, using the overloaded+=operator designed to facilitate this operation.
A simpler way to declare and build dutyOf would have been to write:
KIntVarArray dutyOf(problem, nbPersons, 0, nbDuties-1, ”dutyOf”);
dutyOf = KIntVarArray(problem, nbPersons, 0, nbDuties - 1, 'dutyOf')
KIntVarArray dutyOf = new KIntVarArray(problem,nbPersons,0,nbDuties-1, "dutyOf");
In this case, dutyOf would have been automatically filled with nbPersons KIntVar objects. These ones would have been added to problem and would have had the same possible values between 0 and 3. The only difference between the two methods is the naming scheme. In the first method, we can name our variables whereas in the second one our variables would have been automatically named dutyOf0, dutyOf1, dutyOf2, etc.
The objects in dutyOf can then be accessed using the overloaded [] operator of the class KIntVarArray. For example:
enum People {David, Andrew, Leslie, Jason, Oliver, Michael, Jane, Marylin};
KIntVar myIntVar = dutyOf[Leslie];
myIntVar = KIntVar(dutyOf[peopleNames.index('Leslie')])
KIntVar myIntVar = new KIntVar(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Leslie")));
Here we declare a KIntVar variable named myIntVar and assign to it a copy of the 3rd object lying in dutyOf, returned by the [] operator and representing the location where Leslie will work. Note the use of the enum C++ facility: we strongly recommend the use of enum types to improve the code readability.
Note
The KIntVar objects are pointing to an internal structure where all the information about the state of the variable is stored. For memory issues, this structure is not duplicated when the object is copied: the destination object will be pointing to the same internal structure as the source object. In practice, this means that if the state of our example’s dutyOf[Leslie] object is modified, the state of myIntVar will be modified exactly the same way. In our code, after the copy, we can use either myIntVar or dutyOf[Leslie]. In short: think of KIntVar objects as pointers.
Posting constraints to the problem¶
Constraints are logical relationships between the values of the decision variables that must be satisfied. There are various types of constraints that can be stated using Artelys Kalis (see Reference Manual for a complete list of the different constraint types). These types are represented by various classes, all of them inheriting from the KConstraint class. Here we will see how the constraints we have described in A simple personal planning example can be posted to our KProblem object.
The first constraint states that “each employee must have a unique location”. This constraint has been implicitly posted during the creation of the decision variables. These variables are forced to take a unique value between 0 (ticket office) and 3 (cloakroom).
The 2nd constraint states that “Leslie must work at the second entrance”. The 3rd constraint states that “Michael must work at the first entrance”.
Here is how we can build these constraints:
enum Duties {TicketOffice, EntranceTheater1, EntranceTheater2, CoatCheck};
problem.post( dutyOf[Leslie] == EntranceTheater2 );
problem.post( dutyOf[Michael] == EntranceTheater1 );
Duties = ['TicketOffice', 'EntranceTheater1', 'EntranceTheater2', 'CoatCheck']
problem.post( dutyOf[peopleNames.index('Leslie')] == Duties.index('EntranceTheater2') )
problem.post( dutyOf[peopleNames.index('Michael')] == Duties.index('EntranceTheater1') )
String[] Duties = {"TicketOffice", "EntranceTheater1", "EntranceTheater2", "CoatCheck"};
problem.post( new KEqualXc(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Leslie")), Arrays.asList(Duties).indexOf("EntranceTheater2")));
problem.post( new KEqualXc(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Michael")), Arrays.asList(Duties).indexOf("EntranceTheater1")));
The overloaded == operator applied to the KIntVar dutyOf[Leslie] (or dutyOf[Michael]) and to the integer EntranceTheater2 (or EntranceTheater1) returns a KEqualXc object variable. KEqualXc is the subclass of KConstraint representing the equality between the value of a decision variable and an integer scalar. Then we use the KProblem post() method to add these constraints in problem.
Warning
A constraint will not be taken into account in the problem until the post() method has been called on the associated KConstraint object. Sometimes we want KConstraint objects to state relations between variables that we will use to build other constraints, called composite constraints. For example, “If Oliver is selling tickets, then Marilyn must be with him” is such a constraint, composed of “Oliver is selling tickets” and of “Marilyn is selling tickets”: as we do not necessarily want Oliver nor Marilyn to sell tickets, we will not post these constraints.
The 4th constraint states that “David, Michael and Jason cannot work together”. This means that the locations where they work must all be different. The first idea we could have is to use the overloaded != operator between each possible pair of locations, like this:
problem.post( dutyOf[David] != dutyOf[Michael] );
problem.post( dutyOf[David] != dutyOf[Jason] );
problem.post( dutyOf[Michael] != dutyOf[Jason] );
problem.post( dutyOf[peopleNames.index('David') ] != dutyOf[peopleNames.index('Michael')] )
problem.post( dutyOf[peopleNames.index('David') ] != dutyOf[peopleNames.index('Jason') ] )
problem.post( dutyOf[peopleNames.index('Michael')] != dutyOf[peopleNames.index('Jason') ] )
problem.post( new KNotEqualXyc(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("David")), dutyOf.getElt(Arrays.asList(peopleNames).indexOf("David")),0));
problem.post( new KNotEqualXyc(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("David")), dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Jason")),0));
problem.post( new KNotEqualXyc(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Michael")), dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Jason")),0));
The != operator applied to two decision variables builds an object instantiating the class KNotEqualXyc, which represents inequality constraints. Please note, however, that adding an inequality constraint for each pair of locations is not recommended. Imagine that the “cannot work together” constraint concerns 100 people: we would have to add no less than 4950 inequalities to our problem ! Furthermore, even though these 4950 inequalities are logically equivalent to our unique constraint “These people cannot work together”, they are much less semantically rich.
In order to better express this constraint, we prefer to use an object instantiating KAllDifferent, this way:
KIntVarArray incompatibility;
incompatibility += dutyOf[David];
incompatibility += dutyOf[Michael];
incompatibility += dutyOf[Jason];
problem.post( KAllDifferent(“incompatibility”,incompatibility) );
incompatibility = KIntVarArray()
incompatibility += dutyOf[peopleNames.index('David')]
incompatibility += dutyOf[peopleNames.index('Michael')]
incompatibility += dutyOf[peopleNames.index('Jason')]
problem.post( KAllDifferent('incompatibility',incompatibility) )
KIntVarArray incompatibility = new KIntVarArray();
incompatibility.add(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("David")));
incompatibility.add(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Michael")));
incompatibility.add(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Jason")));
problem.post( new KAllDifferent("incompatibility",incompatibility) );
Since there is no overloaded operator constructing KAllDifferent constraints, we call explicitly the constructor of this class: we build an object of type KAllDifferent names “incompatibility” and apply to the KIntVarArray incompatibility. The latter contains the three decision variables which have to be instantiated to different values.
KAllDifferent represents a global constraint and implements a very efficient algorithm for the propagation of the events on the variables it is applied to. This constraint will be much more efficient in the solving process than our three initial inequalities: this is why we can say that it is semantically richer.
The 5th constraint states that “Each workspace must be occupied by exactly the number of employees it requires”. Actually this constraint is translated with Artelys Kalis in several constraints: one constraint for each location, this way:
int dutiesRequirements[4] = {3,2,2,1};
for(int duty = 0; duty < nbDuties; duty++)
{
problem.post(KOccurTerm(duty,dutyOf) == dutiesRequirements[duty]);
}
dutiesRequirements = [3, 2, 2, 1]
for duty in range(nbDuties):
problem.post(KOccurTerm(duty, dutyOf) == dutiesRequirements[duty])
int[] dutiesRequirements = {3,2,2,1};
for(int duty = 0; duty < nbDuties; duty++)
{
problem.post(new KOccurrence(new KOccurTerm(duty,dutyOf),dutiesRequirements[duty],true,true));
}
For each location duty between 0 and 3, we create a KOccurTerm object, representing the number of occurrences of this location in the instantiated decision variables held by dutyOf. This number of occurrences has to be equal to the number of employees required by this location, so we use the overloaded == operator applied to the KOccurTerm object and to the integer representing the requirement, thus building a KOccurrence object expressing our constraint. As KOccurrence is a subclass of KConstraint, our object can be added to problem using the post() method.
All these occurrence constraints can be resumed by one global constraint KGlobalCardinalityConstraint that implements a more powerful and efficient propagation:
int vals[4] = {0,1,2,3};
int dutiesRequirements[4] = {3,2,2,1};
problem.post(KGlobalCardinalityConstraint("Duty_resources_ctr\0", dutyOf, vals, dutiesRequirements, dutiesRequirements, nbDuties));
vals = [0,1,2,3]
dutiesRequirements = [3,2,2,1]
problem.post(KGlobalCardinalityConstraint("Duty_resources_ctr", dutyOf, vals, dutiesRequirements, dutiesRequirements, nbDuties))
KIntArray dutiesRequirements = new KIntArray();
for (Integer integer1 : Arrays.asList(3, 2, 2, 1))
{
dutiesRequirements.add(integer1);
}
KIntArray vals = new KIntArray();
for (Integer integer : Arrays.asList(0, 1, 2, 3))
{
vals.add(integer);
}
problem.post(new KGlobalCardinalityConstraint("Duty_resources_ctr", dutyOf, vals, dutiesRequirements, dutiesRequirements, nbDuties));
A Global Cardinality Constraint over a set of variables is defined by three arrays called values, lowerBound, and upperBound. The constraint is satisfied if and only if the number of variables of the given set which are assigned to values[i] is greater or equal to lowerBound[i], and lower or equal to upperBound[i] for all i, and if no variable of the given set is assigned to a value which does not belong to values.
Posting a KGlobalCardinalityConstraint to a problem is equivalent, from a modelisation point of view, to posting two instances of KOccurence for each value. But this is absolutely not equivalent from a propagation point of view: Global Cardinality Constraint acquires a far better propagation, using the Regin algorithm.
The last constraint states that “If Oliver is selling tickets, then Marilyn must be with him”. This type of “if…then” constraints can be expressed with Artelys Kalis by using objects of the class KGuard, which take as parameters two constraints and state that if the first is true, then the second is true. For example:
problem.post(KGuard(dutyOf[Oliver] == TicketOffice, dutyOf[Marylin] == TicketOffice));
problem.post(KGuard(dutyOf[peopleNames.index('Oliver')] == Duties.index('TicketOffice'), dutyOf[peopleNames.index('Marylin')] == Duties.index('TicketOffice')))
problem.post(new KGuard(new KEqualXc(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Oliver")),Arrays.asList(Duties).indexOf("TicketOffice")),
new KEqualXc(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Marylin")),Arrays.asList(Duties).indexOf("TicketOffice"))));
Using the overloaded == operator, we build the two KEqualXc constraints “Oliver is selling tickets” and “Marilyn is selling tickets”. These constraints are not added to the problem (because the post() method is not called), but passed as parameters to the KGuard constructor.
Solving the problem¶
Once the problem has been fully built, we can begin to look for solutions. For this, the main class to be used is KSolver, which allows us to:
look for one solution;
look for all solutions;
look for another solution when we already know some of them.
A KSolver object must be associated to a specific problem. Here is how we can declare and create a KSolver which will be associated to our problem:
KSolver mySolver(problem);
mySolver = KSolver(problem)
KSolver mySolver = new KSolver(problem);
When performing its solving functionalities, our object mySolver will store all solutions in the myProblem object. Retrieving these solutions and working on them is the subject of the next section.
In order to find only one solution to our problem, we would write:
mySolver.solve();
mySolver.solve()
mySolver.solve();
The solve() method looks for any valid solution and stores it in the associated KProblem object. But as there may be several different plannings satisfying the constraints, our problem can be solved with different instantiations of the decision variables, i.e. different solutions. If the director wishes to choose between all of these solutions, we can search for them in this way:
mySolver.findAllSolutions();
mySolver.findAllSolutions()
mySolver.findAllSolutions()
The findAllSolutions() method searches for all solutions of the problem and stores them in the associated KProblem object.
When the problem is too large, it can be very time consuming to search for all solutions. If one needs to obtain more than one unique solution, then he should use the KSolver findNextSolution() method. For example:
for(int indexSolution = 0; indexSolution < 5; indexSolution++)
{
mySolver.findNextSolution();
}
mySolver.endLookingForSolution();
for indexSolution in range(5):
mySolver.findNextSolution()
mySolver.endLookingForSolution()
KSolver mySolver = new KSolver(problem);
for(int indexSolution = 0; indexSolution < 5; indexSolution++)
{
mySolver.findNextSolution();
}
mySolver.endLookingForSolution();
The findNextSolution() method searches for solutions which have not yet been found. So the C++ for loop we wrote will find and store five distinct solutions of our problem. The last statement endLookingForSolution() will finalize the tree search and return to the first node of the tree. While it is not called, the branch and bound stay at a node in the tree search and the problem cannot be modified.
Exploring solutions¶
The solutions of the problem are stored in the KProblem object as KSolution objects. This class manages the following information about the solution:
the value of each decision variable in the problem: these values characterize the solution;
the computation time in seconds needed to find this solution;
the number of nodes already opened in the search-tree when this solution was found;
the depth in the search-tree at which this solution was found.
Depending on which method (findNextSolution(), findAllSolutions(), solve() or none) has been used when looking for solutions, the KProblem object can hold any number of KSolution objects. This number can be obtained through the getNumberOfSolutions() method of the KProblem object, this way:
int nbSolutions = problem.getNumberOfSolutions();
nbSolutions = problem.getNumberOfSolutions()
int nbSolutions = problem.getNumberOfSolutions();
The KSolution objects are obtained by using the getSolution() method, this way:
for(int indexSolution = 0; indexSolution < nbSolutions; indexSolution++)
{
KSolution mySolution = problem.getSolution(indexSolution);
mySolution.print();
}
for indexSolution in range(nbSolutions):
mySolution = KSolution(problem.getSolution(indexSolution))
for(int indexSolution = 0; indexSolution < nbSolutions; indexSolution++)
{
KSolution mySolution = problem.getSolution(indexSolution);
mySolution.print();
}
Here we declare a KSolution object named mySolution. In the C++ for loop, we successively retrieve the KSolution objects stored in problem and copy them in mySolution.
In the same for loop, we can get all relevant information about the current solution stored in mySolution. In most cases we are first interested in the values of the decision variables characterizing this solution.
For example, we can get the location occupied by Oliver by this way:
int dutyOfOliver = mySolution.getValue(dutyOf[Oliver]);
dutyOfOliver = mySolution.getValue(dutyOf[peopleNames.index('Oliver')])
int dutyOfOliver = mySolution.getValue(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Oliver")));
We call the KSolution method cpp:func:getValue with the KIntVar parameter dutyOf[Oliver]: getValue() returns the integer value of the decision variable in this solution.
Other information is stored in the KSolution as attributes. These are values computed by Artelys Kalis and stored in each particular KSolution object: they cannot be modified by the user and have only read-access. There are two types of attributes:
double attributes are encoded as C++ double constants and can be read using the
getDblAttrib()methodinteger attributes are encoded as C++ int constants and can be read using the
getIntAttrib()method
You can find below the C++ code to be used to retrieve the value of the three attributes stored in mySolution:
int nbNodes = mySolution.getIntAttrib(KSolver::NumberOfNodes);
int depth = mySolution.getIntAttrib(KSolver::Depth);
double compTime = mySolution.getDblAttrib(KSolver::ComputationTime);
nbNodes = mySolution.getIntAttrib(KSolver.NumberOfNodes)
depth = mySolution.getIntAttrib(KSolver.Depth)
compTime = mySolution.getDblAttrib(KSolver.ComputationTime)
int nbNodes = mySolution.getIntAttrib(KSolver.IntAttrib.NumberOfNodes);
int depth = mySolution.getIntAttrib(KSolver.IntAttrib.Depth);
double compTime = mySolution.getDblAttrib(KSolver.DblAttrib.ComputationTime);
As you can see, both getDblAttrib() and getIntAttrib() take
a unique parameter. This parameter is an integer whose value is in the
KSolver class associated with the relevant identifier. The only things you
have to know are these identifiers: NumberOfNodes, Depth
and ComputationTime (the computation time is expressed in seconds).
They are in “enumerate” structures. Note that there are other classes holding
attributes in Artelys Kalis and that the way to access them will always be the
same: getDblAttrib() or getIntAttrib() applied to an
identifier.
Example summary¶
Below is the complete source code for solving the personnel planning example.
#include "Kalis.h"
// Declaration of people and duties
enum Duties {TicketOffice, EntranceTheater1, EntranceTheater2, CoatCheck};
enum People {David, Andrew, Leslie, Jason, Oliver, Michael, Jane, Marylin};
// *** Main Program ***
int main(void)
{
// Description of datas
int nbPersons = 8;
// Name of each person
char peopleNames[8][20] = {"David", "Andrew", "Leslie", "Jason", "Oliver", "Michael", "Jane", "Marylin"};
// Number of duties
int nbDuties = 4;
// Number of people to be planned for each duty
int dutiesRequirements[4] = {3,2,2,1};
try
{
// Creation of the session
KSession session;
// Creation of the problem "Movie theater" in this session
KProblem problem(session, "Movie Theater");
// Declaration and creation of the array of integer variables dutyOf
// dutyOf[p] is the duty where the person p will be affected
KIntVarArray dutyOf;
// Filling of dutyOf : addition of nbPersons integer variables
// Each variable has a lower bound of 0 ( TicketOffice ) and an upper bound of nbDuties-1 ( CoatCheck )
for(int indexPerson = 0; indexPerson < nbPersons; indexPerson++)
{
dutyOf += KIntVar(problem, peopleNames[indexPerson], 0, nbDuties-1);
}
// Creation of the constraint : "Leslie must be at the second entrance of the theater",
// using '==' overloaded operator
// Post of this constraint in the problem
problem.post(dutyOf[Leslie] == EntranceTheater2);
// Creation of the constraint : "Michael must be at the first entrance of the theater"
// Post of this constraint in the problem
problem.post(dutyOf[Michael] == EntranceTheater1);
// For each duty, creation of the constraint of resource for this duty
// OccurTerm(duty,dutyOf) represents the number of variables in dutyOf that
// will be instantiated to duty
// Post of this constraint
for(int duty = 0; duty < nbDuties; duty++)
{
problem.post(KOccurTerm(duty,dutyOf) == dutiesRequirements[duty]);
}
// Equivalently, one could post one Global Cardinalty Constraint. This implementation is more efficient, implementing a specific algorithm propagation.
//int vals[4] = {0,1,2,3};
//problem.post(KGlobalCardinalityConstraint("Duty_resources_ctr\0", dutyOf, vals, dutiesRequirements, dutiesRequirements, nbDuties));
// Creation of the constraint : "David, Michael and Jason cannot work with each other",
// using explicitly the AllDifferent constraint's constructor
// Post of this constraint
KIntVarArray incompatibility;
incompatibility += dutyOf[David];
incompatibility += dutyOf[Michael];
incompatibility += dutyOf[Jason];
problem.post(KAllDifferent("", incompatibility));
// Creation and post of the constraint : "If Oliver is selling tickets, Marylin must be with him"
problem.post(KGuard(dutyOf[Oliver] == TicketOffice, dutyOf[Marylin] == TicketOffice));
// Specification of the tree search controls to be used in the resolution algorithm
// Declaration and creation of the array of branching schemes
// It will contains the BranchingSchemes objects controlling the tree search
KBranchingSchemeArray myBranchingSchemeArray;
// Creation of an BranchingScheme object of type AssignVar
// - peopleFirst :: It will work of dutyOf[Olivier] and dutyOf[Marylin]
// - SmallestDomain : At each node it will choose between this two variable the one with the smallest domain
// - Nearest : It will choose to assign the nearest value to the target from the variable's domain at this node
// Addition of this branching scheme in the array
KIntVarArray peopleFirst;
peopleFirst += dutyOf[Oliver];
peopleFirst += dutyOf[Marylin];
// setTarget : specify value around which we would like to have our solution (used by Nearest Value Selector)
dutyOf[David].setTarget(2);
dutyOf[Jason].setTarget(0);
dutyOf[Michael].setTarget(1);
dutyOf[Andrew].setTarget(0);
myBranchingSchemeArray += KAssignVar(KSmallestDomain(), KNearestValue());
// Creation of the solver using our tree search controls for this problem
KSolver solver(problem,myBranchingSchemeArray);
// Resolution
// Search of all the solutions to the problem
solver.findAllSolutions();
// Exploration of all the solutions
// Get of the number of solutions
int nbSolutions = problem.getNumberOfSolutions();
// For each solution:
for(int indexSolution = 0; indexSolution < nbSolutions; indexSolution++)
{
// Get the solution and stock it in a Solution object
KSolution solution = problem.getSolution(indexSolution);
// Print the variables values for this solution
printf("Solution %d\n", indexSolution+1);
solution.print();
// Print the computation time the solver needed to find this solution
cout << "Computation time = " << solution.getDblAttrib(KSolver::ComputationTime) << endl;
// Print the number of nodes explored by the solver to find this solution
cout << "Number of nodes = " << solution.getIntAttrib(KSolver::NumberOfNodes) << endl;
// Print the depth of the node where this solution has been found
cout << "Depth = " << solution.getIntAttrib(KSolver::Depth) << endl;
// Print the value of the variable dutyOf[Olivier] in this solution
cout << "dutyOf[Oliver] = " << solution.getValue(dutyOf[Oliver]) << endl;
cout << endl;
}
// Printing global statistics about the resolution
cout << "Solver computation time = " << solver.getDblAttrib(KSolver::ComputationTime) << " s." << endl;
cout << "NumberOfNodes = " << solver.getIntAttrib(KSolver::NumberOfNodes) << endl;
cout << "Depth = " << solver.getIntAttrib(KSolver::Depth) << endl;
cout << "Number of solutions = " << nbSolutions << endl;
cout << "End solving movie theater problem" << endl;
}
catch (ArtelysException &artelysException)
{
// an error occured
cout << "Exception " << artelysException.getCode() << " raised : " << artelysException.getMessage() << endl;
}
return 0;
}
from kalis import *
# ** *Main Program ** *
def main():
# Description of datas
nbPersons = 8
# Name of each person char
peopleNames = ["David", "Andrew", "Leslie", "Jason", "Oliver", "Michael", "Jane", "Marylin"]
# Number of duties int
nbDuties = 4
# Name of each duties
Duties = ['TicketOffice', 'EntranceTheater1', 'EntranceTheater2', 'CoatCheck']
# Number of people to be planned for each duty
dutiesRequirements = [3, 2, 2, 1]
try:
# Creation of the session
session = KSession()
# Creation of the problem "Movie theater" in this session
problem = KProblem(session, "Movie Theater")
# Declaration and creation of the array of integer variables dutyOf
# dutyOf[p] is the duty where the person p will be affected
dutyOf = KIntVarArray()
# Filling of dutyOf: addition of nbPersons integer variables
# Each variable has a lower bound of 0(TicketOffice) and an upper bound of nbDuties - 1(CoatCheck)
for indexPerson in range(nbPersons):
dutyOf += KIntVar(problem, peopleNames[indexPerson], 0, nbDuties - 1)
# Creation of the constraint: "Leslie must be at the second entrance of the theater",
# using '==' overloaded operator
# Post of this constraint in the problem
problem.post(dutyOf[peopleNames.index('Leslie')] == Duties.index('EntranceTheater2'))
# Creation of the constraint: "Michael must be at the first entrance of the theater"
# Post of this constraint in the problem
problem.post(dutyOf[peopleNames.index('Michael')] == Duties.index('EntranceTheater1'))
# For each duty, creation of the constraint of resource for this duty
# OccurTerm(duty, dutyOf) represents the number of variables in dutyOf that
# will be instantiated to duty
# Post of this constraint
for duty in range(nbDuties):
problem.post(KOccurTerm(duty, dutyOf) == dutiesRequirements[duty])
# # Equivalently, one could post one Global Cardinalty Constraint. This implementation is more efficient, implementing a specific algorithm propagation.
# vals = [Duties.index(dutyname) for dutyname in Duties]
# problem.post(KGlobalCardinalityConstraint("Duty_resources_ctr", dutyOf, vals, dutiesRequirements, dutiesRequirements, nbDuties))
# Creation of the constraint: "David, Michael and Jason cannot work with each other",
# using explicitly the AllDifferent constraint 's constructor
# Post of this constraint
incompatibility = KIntVarArray()
incompatibility += dutyOf[peopleNames.index('David')]
incompatibility += dutyOf[peopleNames.index('Michael')]
incompatibility += dutyOf[peopleNames.index('Jason')]
problem.post(KAllDifferent('incompatibility', incompatibility))
# Creation and post of the constraint: "If Oliver is selling tickets, Marylin must be with him"
problem.post(KGuard(dutyOf[peopleNames.index('Oliver')] == Duties.index('TicketOffice'), dutyOf[peopleNames.index('Marylin')] == Duties.index('TicketOffice')))
# Specification of the tree search controls to be used in the resolution algorithm
# Declaration and creation of the array of branching schemes
# It will contains the BranchingSchemes objects controlling the tree search
myBranchingSchemeArray = KBranchingSchemeArray()
# Creation of an BranchingScheme object of type AssignVar
# - peopleFirst:: It will work of dutyOf[Olivier] and dutyOf[Marylin]
# - SmallestDomain: At each node it will choose between this two variable the one with the smallest domain
# - Nearest: It will choose to assign the nearest value to the target from the variable's domain at this node
# Addition of this branching scheme in the array
peopleFirst = KIntVarArray()
peopleFirst += dutyOf[peopleNames.index('Oliver')]
peopleFirst += dutyOf[peopleNames.index('Marylin')]
# setTarget: specify value around which we would like to have our solution(used by Nearest Value Selector)
dutyOf[peopleNames.index('David')].setTarget(2)
dutyOf[peopleNames.index('Jason')].setTarget(0)
dutyOf[peopleNames.index('Michael')].setTarget(1)
dutyOf[peopleNames.index('Andrew')].setTarget(0)
myBranchingSchemeArray += KAssignVar(KSmallestDomain(), KNearestValue())
# Creation of the solver using our tree search controls for this problem
solver = KSolver(problem, myBranchingSchemeArray)
# Resolution
# Search of all the solutions to the problem
solver.findAllSolutions()
# Exploration of all the solutions
# Get of the number of solutions
nbSolutions = problem.getNumberOfSolutions()
# For each solution:
for indexSolution in range(nbSolutions):
# Get the solution and stock it in a Solution object
solution = KSolution(problem.getSolution(indexSolution))
# Print the computation time the solver needed to find this solution
print("Computation time = " + str(solution.getDblAttrib(KSolver.ComputationTime)))
# Print the number of nodes explored by the solver to find this solution
print("Number of nodes = " + str(solution.getIntAttrib(KSolver.NumberOfNodes)))
# Print the depth of the node where this solution has been found
print("Depth = " + str(solution.getIntAttrib(KSolver.Depth)))
# Print the value of the variable dutyOf[Olivier] in this solution
print("dutyOf[Oliver] = " + str(solution.getValue(dutyOf[peopleNames.index('Oliver')])))
# Printing global statistics about the resolution
print("Solver computation time = " + str(solver.getDblAttrib(KSolver.ComputationTime)) + " s.")
print("NumberOfNodes = " + str(solver.getIntAttrib(KSolver.NumberOfNodes)))
print("Depth = " + str(solver.getIntAttrib(KSolver.Depth)))
print("Number of solutions = " + str(nbSolutions))
print("End solving movie theater problem")
except ArtelysException as e:
# an error occured
print("Exception " + str(e))
import com.artelys.kalis.*;
import java.util.Arrays;
import java.util.List;
public class PersonnelPlanning
{
// Description of datas
static int nbPersons = 8;
// Name of each person
static String[] peopleNames = {"David", "Andrew", "Leslie", "Jason", "Oliver", "Michael", "Jane", "Marylin"};
// Number of duties
static int nbDuties = 4;
// Name of each dutie
static String[] Duties = {"TicketOffice", "EntranceTheater1", "EntranceTheater2", "CoatCheck"};
/**
* @param args
*/
public static void main(String[] args)
{
// TODO Auto-generated method stub
System.loadLibrary("KalisJava");
try
{
// Creation of the session
KSession session = new KSession();
// Creation of the problem "Movie theater" in this session
KProblem problem = new KProblem(session, "Movie Theater");
// Declaration and creation of the array of integer variables dutyOf
// dutyOf[p] is the duty where the person p will be affected
KIntVarArray dutyOf = new KIntVarArray();
// Filling of dutyOf : addition of nbPersons integer variables
// Each variable has a lower bound of 0 ( TicketOffice ) and an upper bound of nbDuties-1 ( CoatCheck )
for (int indexPerson = 0; indexPerson < nbPersons; indexPerson++)
{
dutyOf.add(new KIntVar(problem, peopleNames[indexPerson], 0, nbDuties - 1));
}
// Creation of the constraint : "Leslie must be at the second entrance of the theater",
// Post of this constraint in the problem
problem.post(new KEqualXc(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Leslie")), Arrays.asList(Duties).indexOf("EntranceTheater2")));
// Creation of the constraint : "Michael must be at the first entrance of the theater"
// Post of this constraint in the problem
problem.post(new KEqualXc(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Michael")), Arrays.asList(Duties).indexOf("EntranceTheater1")));
// For each duty, creation of the constraint of resource for this duty
// OccurTerm(duty,dutyOf) represents the number of variables in dutyOf that
// will be instantiated to duty
// Post of this constraint
int[] dutiesRequirements_int = new int[]{3, 2, 2, 1};
for (int duty = 0; duty < nbDuties; duty++)
{
problem.post(new KOccurrence(new KOccurTerm(duty, dutyOf), dutiesRequirements_int[duty], true, true));
}
// Equivalently, one could post one Global Cardinalty Constraint. This implementation is more efficient, implementing a specific algorithm propagation.
//KIntArray dutiesRequirements = new KIntArray();
//for (Integer integer1 : Arrays.asList(3, 2, 2, 1))
//{
// dutiesRequirements.add(integer1);
//}
//KIntArray vals = new KIntArray();
//for (Integer integer : Arrays.asList(0, 1, 2, 3))
//{
// vals.add(integer);
//}
// problem.post(new KGlobalCardinalityConstraint("Duty_resources_ctr\0", dutyOf, vals, dutiesRequirements, dutiesRequirements, nbDuties));
// Creation of the constraint : "David, Michael and Jason cannot work with each other",
// using explicitly the AllDifferent constraint's constructor
// Post of this constraint
KIntVarArray incompatibility = new KIntVarArray();
incompatibility.add(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("David")));
incompatibility.add(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Michael")));
incompatibility.add(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Jason")));
problem.post(new KAllDifferent("incompatibility", incompatibility));
// Creation and post of the constraint : "If Oliver is selling tickets, Marylin must be with him"
problem.post(new KGuard(new KEqualXc(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Oliver")), Arrays.asList(Duties).indexOf("TicketOffice")),
new KEqualXc(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Marylin")), Arrays.asList(Duties).indexOf("TicketOffice"))));
// Specification of the tree search controls to be used in the resolution algorithm
// Declaration and creation of the array of branching schemes
// It will contains the BranchingSchemes objects controlling the tree search
KBranchingSchemeArray myBranchingSchemeArray = new KBranchingSchemeArray();
// Creation of an BranchingScheme object of type AssignVar
// - peopleFirst :: It will work of dutyOf[Olivier] and dutyOf[Marylin]
// - SmallestDomain : At each node it will choose between this two variable the one with the smallest domain
// - Nearest : It will choose to assign the nearest value to the target from the variable's domain at this node
// Addition of this branching scheme in the array
KIntVarArray peopleFirst = new KIntVarArray();
peopleFirst.add(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Oliver")));
peopleFirst.add(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Marylin")));
// setTarget : specify value around which we would like to have our solution (used by Nearest Value Selector)
dutyOf.getElt(Arrays.asList(peopleNames).indexOf("David")).setTarget(2);
dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Jason")).setTarget(0);
dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Michael")).setTarget(1);
myBranchingSchemeArray.add(new KAssignVar(new KSmallestDomain(), new KNearestValue()));
// Creation of the solver using our tree search controls for this problem
KSolver solver = new KSolver(problem, myBranchingSchemeArray);
// Resolution
// Search of all the solutions to the problem
solver.findAllSolutions();
// Exploration of all the solutions
// Get of the number of solutions
int nbSolutions = problem.getNumberOfSolutions();
// For each solution:
for (int indexSolution = 0; indexSolution < nbSolutions; indexSolution++)
{
// Get the solution and stock it in a Solution object
KSolution solution = problem.getSolution(indexSolution);
// Print the variables values for this solution
System.out.println("Solution" + indexSolution + 1);
solution.print();
// Print the computation time the solver needed to find this solution
System.out.println("Computation time = " + solution.getDblAttrib(KSolver.DblAttrib.ComputationTime));
// Print the number of nodes explored by the solver to find this solution
System.out.println("Number of nodes = " + solution.getIntAttrib(KSolver.IntAttrib.NumberOfNodes));
// Print the depth of the node where this solution has been found
System.out.println("Depth = " + solution.getIntAttrib(KSolver.IntAttrib.Depth));
// Print the value of the variable dutyOf[Olivier] in this solution
System.out.println("dutyOf[Oliver] = " + solution.getValue(dutyOf.getElt(Arrays.asList(peopleNames).indexOf("Oliver"))));
}
// Printing global statistics about the resolution
System.out.println("Solver computation time = " + solver.getDblAttrib(KSolver.DblAttrib.ComputationTime) + " s.");
System.out.println("NumberOfNodes = " + solver.getIntAttrib(KSolver.IntAttrib.NumberOfNodes));
System.out.println("Depth = " + solver.getIntAttrib(KSolver.IntAttrib.Depth));
System.out.println("Number of solutions = " + nbSolutions);
System.out.println("End solving movie theater problem");
}
catch (Exception e)
{
e.printStackTrace();
}
}
}