Artelys Knitro 11.1 : Résolution ultra-rapide des problèmes sans dérivées !
Cas d’application : Découvrez comment nos clients approximent leurs dérivées en macroéconomie !
La macroéconomie inclut notamment l’étude de modèles nommés DGSE (pour modèles d’Equilibre Général Dynamique Stochastique) qui visent à représenter les effets des politiques économiques sur la croissance d’un pays. Ces modèles sont fréquemment utilisés par les banques centrales pour estimer la croissance nationale globale.
Nous avons travaillé sur les modèles DGSE de la Federal Reserve Bank of New York, implémentés en Matlab avec la toolbox IRIS par Iskander Karibzhanov, économiste pour la Banque du Canada. Ce modèle est un modèle fortement non linéaire pour lequel les dérivées exactes ne peuvent être fournies. Dans ce cas, le solveur approxime les dérivées par différences finies mais il n’est pas possible de les évaluer avec autant de précision que lorsque les dérivées exactes sont fournies.
La parallélisation des différences finies avec Artelys Knitro permet d’accélérer la résolution. L’utilisation de Knitro 11.1 a permis de réduire le temps de calcul d’un facteur 5 sur les instances étudiées tout en maintenant la qualité de la solution obtenue !

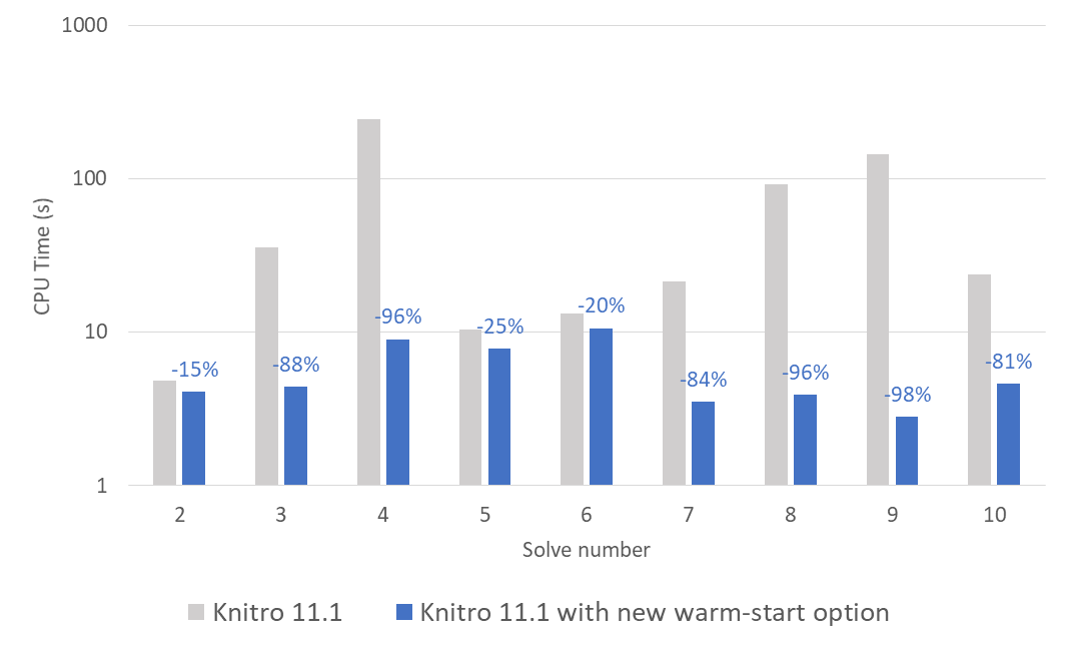
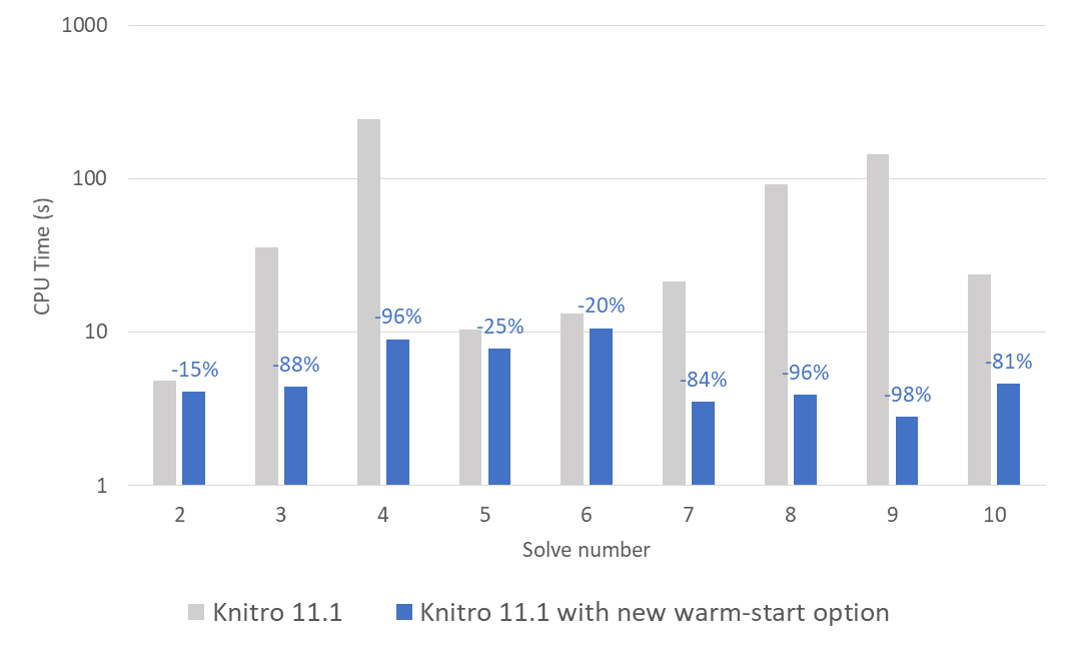
Nouvelle option de warm-start pour les méthodes de points intérieurs
Cette version voit également l’apparition d’une nouvelle option dédiée au warm-start pour les méthodes de points intérieurs (algorithmes 1&2). L’activation de cette option permet une résolution ultra-rapide de vos problèmes lorsque l’utilisateur a la connaissance d’un bon point initial. Cette option est particulièrement efficace pour les modèles nécessitant la résolution séquentielle de problèmes non linéaires. La figure ci-dessous présente un cas d’application nécessitant la résolution séquentielle de sous-problèmes non linéaires pour laquelle l’activation de l’option de warm-start divise le temps de calcul total par 10 !
Autres fonctionnalités d’Artelys Knitro 11.1
• Nouvelle API Python permettant une déclaration fine de la structure des contraintes (eg linéaire, quadratique, conique)
• Détection automatique de la convexité des problèmes QP/QCQP
• Nouvelles coupes de sac à dos liftées dédiées aux problèmes MINLP
• Amélioration de l’approximation L-BFGS
• Augmentation générale des performances sur les problèmes convexes en particulier pour les instances de très grande taille

Swissgrid sélectionne Artelys Crystal Super Grid
Artelys a le plaisir d’annoncer que Swissgrid, le Gestionnaire du Réseau de Transport (GRT) d’électricité suisse, a choisi Artelys Crystal Super Grid, notre solution de simulation multi-énergies, pour réaliser ses activités de planification stratégique et d’analyse du système électrique.

Artelys a mené l’évaluation des options de politiques visant à sécuriser l’inertie, pour la Commission Européenne
La direction générale de l’énergie (DG ENER) de la Commission Européenne a retenu Artelys (leader), Trinomics et Tractebel ENGIE pour étudier les solutions permettant d’assurer la stabilité en fréquence du système électrique européen à l’avenir. Le rapport de l’étude...

Artelys Knitro 15.0 : De nouveaux outils pour vos modèles de grande taille
Artelys est heureux d’annoncer la sortie de Knitro 15.0, qui met à disposition de nouveaux algorithmes et ainsi des améliorations de performances permettant de résoudre plus rapidement vos problèmes d’optimisation de grande taille, qu’ils soient linéaires ou non-linéaires.

Artelys développe Future Sight : un outil de visualisation au service de la transition énergétique
En tant que partenaire du « European Climate + Energy Modeling Forum » (ECEMF) – un projet Horizon 2020 Europe réunissant des instituts de recherche et des experts en modélisation énergétiques de premier plan en Europe – Artelys a contribué aux activités de modélisation alimentées par l’outil de modélisation Artelys Crystal Super Grid, et a dirigé le développement d’un outil de visualisation à part entière.