Tips and tricks
This last chapter contains some rules of the thumb to improve efficiency, solve memory issues and other frequent problems.
Automatic Differentiation (AD)
Why is Automatic Differentiation important?
Nonlinear optimization software relies on accurate and efficient derivative computations for faster solutions and improved robustness.
Knitro in particular has the ability to utilize second derivative (Hessian matrix) information for faster convergence. Computing partial derivatives and coding them manually in a programming language can be time consuming and error prone (Knitro does provide a function to check first derivatives against finite differences).
Automatic Differentiation (AD) is a modern technique which automatically and efficiently computes the exact derivatives so that the user is freed from dealing with this issue.
Most modeling languages provide automatic differentiation.
Option tuning for efficiency
If you are unsure how to set non-default options, or which user options to play with, simply running your model with the setting
tuner=1 will cause the Knitro-Tuner to run many instances of your model with a variety of option settings, and report some statistics and recommendations on what non-default option settings may improve performance on your model. Often significant performance improvements may be made by choosing non-default option settings. See The Knitro-Tuner for more details.The most important user option is the choice of which continuous nonlinear optimization algorithm to use, which is specified by the
algorithmoption. Please try all four options as it is often difficult to predict which one will work best, or try using the multi option (algorithm=5). In particular the Active Set algorithms may often work best for small problems, problems whose only constraints are simple bounds on the variables, or linear programs. The interior-point algorithms are generally preferable for large-scale problems.Perhaps the second most important user option setting is the
hessoptuser option that specifies which Hessian (or Hessian approximation) technique to use. If you (or the modeling language) are not providing the exact Hessian to Knitro, then you should experiment with different values here.One of the most important user options for the interior-point algorithms is the
bar_muruleoption, which controls the handling of the barrier parameter. It is recommended to experiment with different values for this user option if you are using one of the interior-point solvers in Knitro.If you are using the Interior/Direct algorithm and it seems to be taking a large number of conjugate gradient (CG) steps (as evidenced by a non-zero value under the CGits output column header on many iterations), then you should try a small value for the
bar_directintervaluser option (e.g., 0-2). This option will try to prevent Knitro from taking an excessive number of CG steps. Additionally, if there are solver iterations where Knitro slows down because it is taking a very large number of CG iterations, you can try enforcing a maximum limit on the number of CG iterations per algorithm iteration using thecg_maxituser option.The
linsolveroption can make a big difference in performance for some problems. For small problems (particularly small problems with dense Jacobian and Hessian matrices), it is recommended to try the qr, ma27, hyrbrid, and ma57 settings. For large problems, it is recommended to try the ma57, mklpardiso, ma97, and ma86 settings to see which is fastest. It is highly recommended to use an optimized BLAS, such as the Intel MKL BLAS (blasoption= 1) provided with Knitro, as this can result in significant speedups compared to the internal Knitro BLAS (blasoption= 0).When solving mixed integer problems (MIPs), if Knitro is struggling to find an integer feasible point, then you should try different values for the
mip_heuristic_strategyoption, and also experiment with enabling other mip_heuristic_ options, which will search for integer feasible points. Other important MIP options that can significantly impact the performance of Knitro are themip_method,mip_branchrule, andmip_selectruleuser options, as well as themip_nodealgoption which will determine the Knitro algorithm to use to solve the nonlinear, continuous subproblems generated during the branch-and-bound process.
Setting bounds efficiently
Why is Knitro not honoring my bound constraints?
By default Knitro does not enforce that simple bounds on the variables (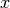 )
are satisfied throughout the optimization process. Rather, satisfaction of these bounds is only enforced at the solution
(within some feasibility tolerance).
)
are satisfied throughout the optimization process. Rather, satisfaction of these bounds is only enforced at the solution
(within some feasibility tolerance).
In some applications, however, the user may want to enforce that the initial point and all intermediate iterates satisfy the
bounds 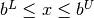 .
This can be enforced by setting
.
This can be enforced by setting KN_PARAM_HONORBNDS to 1.
Please note, the honor bounds option pertains only to the simple bounds defined with vectors 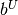 and
and 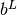 for
for 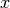 ,
not to the general equality and inequality constraints defined with the vectors
,
not to the general equality and inequality constraints defined with the vectors 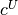 ,
, 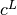 , and
, and  .
.
Do I need to specify a constraint with 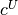 ,
, 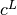 , and
, and  if I already specified it with the bounds parameters
if I already specified it with the bounds parameters 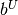 and
and 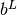 ?
?
No, if you have specified a constraint with the bounds parameters then you should not specify it with the general constraints.
For example, 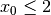 is best modeled by setting
is best modeled by setting 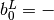
KN_INFINITY and 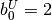 .
.
Duplicate specification of a constraint can make the problem more difficult to solve.
Do I need to initialize all of the bounds parameters? What if a variable is unbounded?
You only need to initialize finite bounds in your model using the API functions
KN_set_var_lobnds(),
KN_set_var_upbnds(), and KN_set_var_fxbnds(). Any variable bounds that are
not explicitly set are infinite (i.e. unbounded).
You can also explicitly mark infinite bounds using the API functions above by using
Knitro’s value for infinity, KN_INFINITY to denote unbounded.
Note that any finite variable bound larger than bndrange() in magnitude will be
treated as infinite by Knitro. To treat it as a real finite bound, you must either
increase the value of bndrange() to be larger than the largest finite
bound, or rescale the problem to make the finite bounds smaller in magnitude.
See include/knitro.h for the definition of KN_INFINITY.
Do I need to initialize all of the constraint parameters 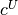 and
and 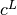 ? What if a constraint is unbounded?
? What if a constraint is unbounded?
You only need to initialize finite bounds in your model using the API functions
KN_set_con_lobnds(),
KN_set_con_upbnds(), and KN_set_con_eqbnds(). Any constraint bounds that are
not explicitly set are infinite (i.e. unbounded).
You can also explicitly mark infinite bounds using the API functions above by using
Knitro’s value for infinity, KN_INFINITY to denote unbounded.
Note that any finite constraint bound larger than bndrange() in magnitude will be
treated as infinite by Knitro. To treat it as a real finite bound, you must either
increase the value of bndrange() to be larger than the largest finite
bound, or rescale the problem to make the finite bounds smaller in magnitude.
See include/knitro.h for the definition of KN_INFINITY.
Memory issues
If you receive a Knitro termination message indicating that there was not enough memory on your computer to solve the problem, or if your problem appears to be running very slow because it is using nearly all of the available memory on your computer system, the following are some recommendations to try to reduce the amount of memory used by Knitro.
Experiment with different algorithms. Typically the Interior/Direct algorithm is chosen by default and uses the most memory. The Interior/CG and Active Set algorithms usually use much less memory. In particular if the Hessian matrix is large and dense and using most of the memory, then the Interior/CG method may offer big savings in memory. If the constraint Jacobian matrix is large and dense and using most of the memory, then the Active Set algorithm may use much less memory on your problem.
When using the default Interior/Direct algorithm, try setting the option
bar_linsys_storage= lowmem (1).If much of the memory usage seems to come from the Hessian matrix, then you should try different Hessian options via the
hessoptuser option. In particularhessoptsettings product_findiff, product, and lbfgs use the least amount of memory.Try different linear solver options in Knitro via the
linsolveruser option. Sometimes even if your problem definition (e.g. Hessian and Jacobian matrix) can be easily stored in memory, the sparse linear system solvers inside Knitro may require a lot of extra memory to perform and store matrix factorizations. For large problems you should try ma57, mklpardiso, ma97, and ma86, as one of these may use significantly less memory than the default option on some models. In addition, using a smallerlinsolver_pivottoluser option value may reduce the amount of memory needed for the linear solver.
Reproducibility issues across platform/computer
If you notice different results across different platforms/computers for the exact same Knitro run (same model, same initial conditions, same options), it is probably due to one of the following reasons:
The Knitro library is built with different compilers on different operating systems, which can cause small numerical differences that propagate.
The Intel MKL library has specializations to optimize performance for particular hardware/CPUs/environments which can also cause numerical differences.
To avoid the second issue you may set cpuplatform = compatible (1). If this doesn’t work, you may also try
setting blasoption = 0 to use internal Knitro BLAS functions (instead of the Intel MKL library), but note that
this may result in much slower performance.