Problem modification and re-solving

After invoking KN_solve() to perform an initial solve of the model, you may wish to make some small modifications to your model and then re-solve. This section outlines the modifications that can be made to an existing model after an initial solve, which allow for re-solving the existing model using the same Knitro solver instance.

Generally, as long as no structural changes beyond linear changes are made to the model, KN_solve() can be called in succession to re-solve a model after modifications. For example, user options, variable bounds, and constraint bounds can be changed between calls to KN_solve(), without having to first call KN_free() and reload the model from scratch. In addition, constant and linear structures in the model may be added, deleted, or changed without having to reconstruct the model. More extensive additions or changes to the model (such as adding quadratic structures or callbacks) require freeing the existing Knitro solver object and rebuilding the model from scratch.

More specifically, the following API functions may be used to modify a problem before re-solving.

Any user parameters may be changed before solving again via calls to KN_set_int_param(), KN_set_double_param() or similar API functions for setting user parameters.
The initial point may be set via calls to KN_set_var_primal_init_values(), KN_set_var_dual_init_values(), KN_set_con_dual_init_values(), or similar functions. If the initial point is not set using one of these functions, the re-solve will automatically use the solution of the previously solved problem as the initial point for the next solve.
Variable bounds may be changed via calls to KN_set_var_lobnds(), KN_set_var_upbnds(), KN_set_var_fxbnds() or similar API functions.
Variable types may be changed via calls to KN_set_var_types(), or similar API functions.
Constraint bounds may be changed via calls to KN_set_con_lobnds(), KN_set_con_upbnds(), KN_set_con_eqbnds() or similar API functions.
Constant structure for the objective or constraints may be added, deleted or changed using the API functions KN_add_obj_constant(), KN_del_obj_constant(), KN_chg_obj_constant(), KN_add_con_constants(), KN_del_con_constants(), and KN_chg_con_constants() and related API functions.
Linear structures for the objective or constraints may be added, deleted or changed using the API functions KN_add_obj_linear_struct(), KN_del_obj_linear_struct(), KN_chg_obj_linear_struct(), KN_add_con_linear_struct(), KN_del_con_linear_struct(), and KN_chg_con_linear_struct() and related API functions.
KN_add_vars()/KN_add_var() may be used to add new variables that will only appear in linear terms to the model. After adding the new variables, the API functions for adding linear structures described above may be used to add new linear terms involving these variables to the objective or constraints.
KN_add_cons()/KN_add_con() may be used to add new linear constraints to the model. After adding the new constraints, the API functions for adding constant or linear structures described above may be used to add constant or linear terms to these new constraints.

There are a few important points to note regarding problem modification.

The constant and linear structural changes in the model implemented through KN_add_*(), KN_del_*(), and KN_chg_*() functions are not actually updated until KN_solve() or KN_update() is called. Therefore, any API functions that retrieve these problem structures will not reflect any new changes made since the last call to KN_solve() or KN_update(). In contrast, typically model changes implemented through KN_set_*() functions (such as setting variable or constraint bounds) are updated immediately.
API functions that delete problem structure can only be used to delete structure that existed in the model prior to the last call to KN_solve() or KN_update(). Any new structure added since the last call to KN_solve() or KN_update() cannot be deleted. In practice, there would be no reason to delete such structure, since you can just avoid adding it in the first place if it is not wanted.
API functions for changing structures are just shorthand for deleting and then adding new structures. For example, if you want to change an existing linear constraint coefficient, calling KN_chg_con_linear_struct() is identical to calling KN_del_con_linear_struct() followed by KN_add_con_linear_struct() on that coefficient.
Although there is not currently an API function to directly remove linear constraints (Knitro API functions work on structures, rather than constraints), a linear constraint will effectively be removed by calling the API functions KN_del_con_constants() and KN_del_con_linear_struct() to remove all the constant and linear structures in the constraint, and removing any existing constraint bounds (by setting the lower constraint bound to -KN_INFINITY and the upper constraint bound to KN_INFINITY if necessary).

For more details on the API functions described above, please see the callable library API section in the Reference Manual Callable library API reference. Below we provide a simple example, demonstrating how to modify and then re-solve a problem using the same problem context structure. More examples may be found in the Knitro distribution examples/C directory.

Example

Consider the following nonlinear optimization problem from the Hock and Schittkowski test set provided as example examples/C/exampleNLP2.c.

max   x0*x1*x2*x3         (obj)
s.t.  x0^3 + x1^2 = 1     (c0)
      x0^2*x3 - x2 = 0    (c1)
      x3^2 - x1 = 0       (c2)

In examples/C/exampleNLP2Resolve.c and below, we show how to modify this problem by adding, deleting, or changing linear structures in the model, and then re-solve using the same Knitro solver instance.

Note

The Knitro distribution comes with several C language programs in the directory examples/C. The instructions in examples/C/README.txt explain how to compile and run the examples.

We will not repeat the code for solving the original model above. This is covered in the example from section Derivatives and in file examples/C/exampleNLP2.c.

In the code segments below, we show the modifications made after the initial call to KN_solve().

First, after the initial solve, we add a new linear term 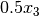$0.5 x_3$ to (c2), and add a new linear inequality constraint (c3) so the model becomes:

max   x0*x1*x2*x3             (obj)
s.t.  x0^3 + x1^2 = 1         (c0)
      x0^2*x3 - x2 = 0        (c1)
      x3^2 - x1 + 0.5x3 = 0   (c2)
      x1 + 2x2 + x3 <= 2.5    (c3)

Then it is re-solved using the same kc structure.

/*... Solve the initial problem. ...*/
nStatus = KN_solve (kc);


/*=============== MODIFY PROBLEM AND RE-SOLVE ===========*/

/** Add 0.5x3 linear term to c2 */
nVar = 3;
dCoef = 0.5;
error = KN_add_con_linear_struct_one (kc, 1, 2,
                                      &nVar,
                                      &dCoef);
if (error) exit(-1);

/** Now add a new linear constraint
 *    x1 + 2x2 + x3 <= 2.5 (c3)
 *  and re-solve. */
error = KN_add_con(kc, &cIndNew);
if (error) exit(-1);
error = KN_set_con_upbnd(kc, cIndNew, 2.5);
if (error) exit(-1);
/** Coefficients for 3 linear terms */
lconNewIndexVars[0] = 1; lconNewCoefs[0] = 1.0;
lconNewIndexVars[1] = 2; lconNewCoefs[1] = 2.0;
lconNewIndexVars[2] = 3; lconNewCoefs[2] = 1.0;
error = KN_add_con_linear_struct_one (kc, 3, cIndNew,
                                      lconNewIndexVars,
                                      lconNewCoefs);
if (error) exit(-1);

/** Tell Knitro to try a "warm-start" since it is starting from the solution
 *  of the previous solve, which may be a good initial point for the solution
 *  of the slightly modified problem. */
error = KN_set_int_param (kc, KN_PARAM_STRAT_WARM_START, KN_STRAT_WARM_START_YES);

/** Re-solve the modified problem. */
nStatus = KN_solve (kc);

Next we remove the linear term 0.5x3 from (c2), and change the linear term x1 in c(3) to be 3.5x1 so the model becomes

max   x0*x1*x2*x3             (obj)
s.t.  x0^3 + x1^2 = 1         (c0)
      x0^2*x3 - x2 = 0        (c1)
      x3^2 - x1 = 0           (c2)
      3.5x1 + 2x2 + x3 <= 2.5 (c3)

/*=============== MODIFY PROBLEM AND RE-SOLVE AGAIN ===========*/

/** Delete 0.5x3 linear term from c2 */
nVar = 3;
error = KN_del_con_linear_struct_one (kc, 1, 2,
                                      &nVar);
if (error) exit(-1);

/** Change x1 linear term in c3 to 3.5*x1 */
nVar = 1;
dCoef = 3.5;
error = KN_chg_con_linear_struct_one (kc, 1, 3,
                                      &nVar, &dCoef);
if (error) exit(-1);

/** Re-solve the modified problem again. */
nStatus = KN_solve (kc);