Multi-Start¶
Nonlinear optimization problems are often non-convex due to the
objective function, constraint functions, or both. When this is true, there
may be many points that satisfy the local optimality conditions.
Default Knitro behavior is to return the
first locally optimal point found. Knitro offers a simple
multi-start feature that searches for a better optimal point by
restarting Knitro from different initial points. The feature is
enabled by setting ms_enable = 1.
Note
In many cases the user would like to obtain the global optimum to the optimization problem; that is, the local optimum with the very best objective function value. Knitro cannot guarantee that multi-start will find the global optimum. In general, the global optimum can only be found with special knowledge of the objective and constraint functions; for example, the functions may need to be bounded by other piece-wise convex functions. Knitro executes with very little information about functional form. Although no guarantee can be made, the probability of finding a better local solution improves if more start points are tried.
Multi-Start algorithm¶
The multi-start procedure generates new start points by randomly selecting
components of x that satisfy lower and upper bounds on the variables.
Knitro finds a local optimum from each start point using the same
problem definition and user options.
The final solution returned from KN_solve() is the local optimum
with the best objective function value if any local optima have been found.
If no local optimum has been found, Knitro will return the best
feasible solution estimate it found. If no feasible solution estimate has
been found, Knitro will return the least infeasible point.
Parallel multi-start¶
The multi-start procedure can run in parallel on shared memory
multi-processor machines by setting numthreads greater
than 1. See Parallelism for more details on controlling
parallel performance in Knitro.
The option ms_numthreads can be used to set the number
of threads used specifically by the multi-start procedure. For instance, if
numthreads =16 and ms_numthreads =8,
Knitro will run 8 solves in parallel and each solve will be
allocated 2 threads.
The Knitro multi-start procedure is deterministic, even when
run in parallel using multiple threads. Unless it terminates
due to some time limit, it should always produce the same results.
The ms_terminate option can be used to control how the
multi-start procedure terminates. It can terminate after a preset
number of local solves (specified by ms_maxsolves), or
after the first locally optimal (or feasible) solution estimate is
found. By default the multi-start procedure will automatically terminate when
the probability of finding new local solutions is small (unless it reaches
the ms_maxsolves limit first). The option,
ms_terminaterule_tol,
can be used to control how quickly termination is triggered in this case.
Multi-Start output¶
For multi-start, you can have output from each local solve written to a file
named knitro_ms_x.log where “x” is the solve number by setting
the option ms_outsub=1.
Multi-Start options¶
The multi-start option is convenient for conducting a simple search for
a better solution point. Search time is improved if the variable bounds
are made as tight as possible, confining the search to a region where a
good solution is likely to be found. The user can restrict the multi-start
search region without altering bounds by using the options
ms_maxbndrange and ms_startptrange. The other multi-start
options are the following.
Option |
Meaning |
|---|---|
Enable multi-start |
|
Clustering strategy for multi-start |
|
Maximum unbounded variable range for multi-start |
|
Maximum Knitro solves for multi-start |
|
Feasible points to save from multi-start |
|
Specify number of threads for parallel multi-start |
|
Can write each solve to a file (parallel only) |
|
Tol for feasible points being equal |
|
Initial seed for generating random start points |
|
Maximum variable range for multi-start |
|
Maximum real time for multi-start subproblems, in seconds |
|
Termination condition for multi-start |
|
Tolerance for the rule-based termination of multi-start |
The number of start points tried by multi-start is specified with the
option ms_maxsolves. By default, for continuous models, Knitro will try
min(100, 10*n), where n is the number of variables in the problem. When applied to
node subproblems inside the branch-and-bound algorithm for mixed-integer problems,
Knitro will try 8 multi-start points by default.
Users may override the default by setting ms_maxsolves to
a specific value.
The ms_maxbndrange option applies to variables unbounded in at least one direction
(i.e., the upper or lower bound, or both, is infinite)
and keeps new start points within a total range equal to the value of
ms_maxbndrange.
The ms_startptrange option applies to all variables and keeps new start points within
a total range equal to the value of ms_startptrange, overruling
ms_maxbndrange if it is a tighter bound.
In general, use ms_startptrange to limit the multi-start search
only if the initial start point supplied by the user is known to be the center
of a desired search area. Use ms_maxbndrange as a surrogate bound
to limit the multi-start search when a variable is unbounded.
The ms_num_to_save option
allows a specific number of distinct feasible points to be saved in a file named
knitro_mspoints.log. Each point results from a Knitro solve
from a different starting point, and must satisfy the absolute and relative
feasibility tolerances. Different start points may return the same feasible
point, and the file contains only distinct points. The option
ms_savetol determines that two points are distinct if their
objectives or any solution components (including Lagrange multipliers)
are separated by more than the value of
ms_savetol using a relative tolerance test.
More specifically, two values x and y are considered distinct if:
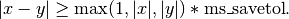
The file stores points in order from best objective to worst. If objectives
are the same (as defined by ms_savetol), then points are
ordered from smallest feasibility error to largest. The file can be read
manually, but conforms to a fixed property/value format for machine reading.
Instead of using multi-start to search for a global solution, a user may want to
use multi-start as a mechanism for finding any locally optimal or feasible solution
estimate of a non-convex problem and terminate as soon as one such point is found.
The ms_terminate option, provides the user more control over when to terminate
the multi-start procedure.
If ms_terminate = optimal the multi-start procedure will stop as soon as
the first locally optimal solution is found or after ms_maxsolves
– whichever comes first. If ms_terminate = feasible the multi-start
procedure will instead stop as soon as the first feasible solution estimate is found
or after ms_maxsolves – whichever comes first. If
ms_terminate = maxsolves, it will only terminate after ms_maxsolves.
If ms_terminate = rulebased, the multi-start procedure will stop when the
probability of finding new local solutions seems low based on some rules,
or after ms_maxsolves – whichever comes first.
The option ms_seed can be used to change the seed used to generate the random
initial points for multi-start.
Multi-Start callbacks¶
The multi-start procedure provides two callback utilities for the callable library API.
int KNITRO_API KN_set_ms_process_callback (KN_context_ptr kc,
KN_user_callback * const fnPtr,
void * const userParams);
int KNITRO_API KN_set_ms_initpt_callback (KN_context_ptr kc,
KN_ms_initpt_callback * const fnPtr,
void * const userParams);
The first callback can be used to perform some user task after each multi-start solve
and is set by calling KN_set_ms_process_callback(). You can use the second
callback to specify your own initial points for multi-start instead of using the
randomly generated Knitro initial points. This callback function can be set through the
function KN_set_ms_initpt_callback().
See the Callable library API reference section in the Reference Manual for details on setting these callback functions and the prototypes for these callback functions.
AMPL example¶
Let us consider again our AMPL example from Section Getting started with AMPL and run it with a different set of options:
1ampl: reset;
2ampl: option solver knitroampl;
3ampl: option knitro_options "ms_enable=1 ms_num_to_save=5 ms_savetol=0.01";
4ampl: model testproblem.mod;
5ampl: solve;
The Knitro log printed on screen changes to reflect the results of the many solver runs that were made during the multi-start procedure, and the very end of this log reads:
Multistart stopping, reached ms_maxsolves limit.
MULTISTART: Best locally optimal point is returned.
EXIT: Locally optimal solution found.
Final Statistics
----------------
Final objective value = 9.36000000004473e+02
Final feasibility error (abs / rel) = 7.11e-15 / 3.29e-18
Final optimality error (abs / rel) = 3.51e-08 / 1.38e-08
# of iterations = 582
# of CG iterations = 120
# of function evaluations = 0
# of gradient evaluations = 0
# of Hessian evaluations = 0
Total program time (secs) = 0.01360 ( 0.050 CPU time)
===============================================================================
Knitro 15.1.0: Locally optimal or satisfactory solution.
objective 936.000000004473; feasibility error 7.11e-15
582 iterations; 0 function evaluations
which shows that many more iterations were needed than without
multi-start. A file knitro_mspoints.txt was also created,
whose content reads:
// Knitro 15.1.0 Multi-start Repository for feasible points.
// Each point contains information about the problem and the point.
// Points are sorted by objective value, from best to worst.
// Next feasible point.
numVars = 3
numCons = 2
objGoal = MINIMIZE
obj = 9.3600000342420878e+02
knitroStatus = 0
localSolveNumber = 1
feasibleErrorAbsolute = 0.00e+00
feasibleErrorRelative = 0.00e+00
optimalityErrorAbsolute = 2.25e-07
optimalityErrorRelative = 1.41e-08
x[0] = 2.0511214409048425e-07
x[1] = 4.1077619358921463e-08
x[2] = 7.9999996834308824e+00
lambda[0] = -4.5247620510168322e-08
lambda[1] = 2.2857143915699769e+00
lambda[2] = -1.0285715141992103e+01
lambda[3] = -3.2000001143071813e+01
lambda[4] = -2.1985040913238130e-07
// Next feasible point.
numVars = 3
numCons = 2
objGoal = MINIMIZE
obj = 9.5100000269458542e+02
knitroStatus = 0
localSolveNumber = 2
feasibleErrorAbsolute = 0.00e+00
feasibleErrorRelative = 0.00e+00
optimalityErrorAbsolute = 3.67e-07
optimalityErrorRelative = 2.62e-08
x[0] = 6.9999996377946481e+00
x[1] = 7.4479065893720198e-08
x[2] = 2.6499084231411754e-07
lambda[0] = -6.3891336872934633e-08
lambda[1] = 1.7500001368019027e+00
lambda[2] = -2.1791026695882249e-07
lambda[3] = -1.7500002055167382e+01
lambda[4] = -5.2500010586300956e+00
In addition to the known solution with value 936 that we had already found with a single solver run, we discover another local minimum with value 951 that we had never seen before. In this case, the new solution is not as good as the first one, but sometimes running the multi-start algorithm significantly improves the objective function value with respect to single-run optimization.
MATLAB example¶
In order to run the multi-start algorithm in MATLAB, we must pass
the relevant set of options to Knitro via the Knitro options file.
Let us create a simple text file named knitro.opt with the
following content:
ms_enable 1
ms_num_to_save 5
ms_savetol 0.01
hessopt 2
(the last line hessopt 2 is necessary to remind Knitro to use approximate second derivatives, since we are not providing the exact hessian). Then let us run our MATLAB example from Section MATLAB example again, where the call to knitro_nlp has been replaced with:
knitro_nlp(@obj, x0, A, b, Aeq, beq, lb, ub, @nlcon, [], options, 'knitro.opt');
and where the knitro.opt file was placed in the current directory so that
MATLAB can find it. The Knitro log looks similar to what we observed with AMPL.
C example¶
The C example can also be easily modified to enable
multi-start by adding the following lines before the
call to KN_solve():
// multistart
if (KN_set_int_param_by_name (kc, "ms_enable", 1) != 0)
exit( -1 );
if (KN_set_int_param_by_name (kc, "ms_num_to_save", 5) != 0)
exit( -1 );
if (KN_set_double_param_by_name (kc, "ms_savetol", 0.01) != 0)
exit( -1 );
Again, running this example we get a Knitro log that looks similar to what we observed with AMPL.
Object-oriented example¶
The object-oriented example can be modified to enable
multi-start by adding the following lines before the
call to solver.solve():
// multistart
solver.setParam("ms_enable", 1);
solver.setParam("ms_num_to_save", 5);
solver.setParam("ms_savetol", 0.01);
Again, running this example we get a Knitro log that looks similar to the trace obtained with AMPL.