Nonlinear Least-Squares
Knitro provides a specialized API for nonlinear least-squares models of the following form:
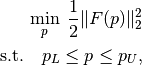
where 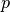 is a parameter to be optimized and
is a parameter to be optimized and 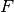 is a differentiable function,
which is called a residual.
This type of problem appears very often in statistics, data-mining and machine learning.
Using the nonlinear least-squares API, you are able to model a nonlinear least-squares
problem in standard form above and use the Gauss-Newton Hessian option.
is a differentiable function,
which is called a residual.
This type of problem appears very often in statistics, data-mining and machine learning.
Using the nonlinear least-squares API, you are able to model a nonlinear least-squares
problem in standard form above and use the Gauss-Newton Hessian option.
The Gauss-Newton Hessian provides a positive semi-definite Hessian approximation 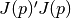 (where
(where 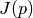 is the Jacobian matrix of the residual functions
is the Jacobian matrix of the residual functions 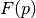 ) at every
iteration and has good local convergence properties in practice.
The Gauss-Newton Hessian option
) at every
iteration and has good local convergence properties in practice.
The Gauss-Newton Hessian option KN_HESSOPT_GAUSS_NEWTON, is the default Hessian option
when using the nonlinear least-squares API. The quasi-Newton Hessian options are also available
through the least-squares API, however, the user-supplied exact Hessian can only be specified
using the standard API.
Any of the Knitro nonlinear algorithms can be used through the least-squares API.
Knitro will behave like a Gauss-Newton method by using the
linesearch methods nlp_algorithm = KN_NLP_ALG_BAR_DIRECT or KN_NLP_ALG_ACT_SQP,
and will be very similar to the classical Levenberg-Marquardt method when
using the trust-region methods nlp_algorithm = KN_NLP_ALG_BAR_CG or KN_NLP_ALG_ACT_CG.
Residuals are added to a least-squares model using the KN_add_rsds().
The coefficients and sparsity structure for linear residuals (or linear terms inside
nonlinear residuals) can be provided to
Knitro throught the API function KN_add_rsd_linear_struct().
Constants can be added to residuals through KN_add_rsd_constants().
The nonlinear residuals and Jacobian are provided to Knitro using the callback functions
KN_add_lsq_eval_callback() and KN_set_cb_rsd_jac() described below.
Each user callback routine should return an int value of 0 if successful, or a negative
value to indicate that an error occurred during execution of the user-provided function.
If a callback function to evaluate the residual Jacobian is not provided, Knitro
will approximate it using finite-differences.
Please see Callable library API reference for more details on these API functions.
/** Add an evaluation callback for a least-squares models. Similar to KN_add_eval_callback()
* but for least-squares models.
*
* nR - number of residuals evaluated in the callback
* indexRsds - (length nR) index of residuals evaluated in the callback
* rsdCallback - a pointer to a function that evaluates any residual parts
* (specified by nR and indexRsds) involved in this callback
* cb - (output) the callback structure that gets created by
* calling this function; all the memory for this structure is
* handled by Knitro
*
* After a callback is created by "KN_add_lsq_eval_callback()", the user can then
* specify residual Jacobian information and structure through "KN_set_cb_rsd_jac()".
* If not set, Knitro will approximate the residual Jacobian. However, it is highly
* recommended to provide a callback routine to specify the residual Jacobian if at all
* possible as this will greatly improve the performance of Knitro. Even if a callback
* for the residual Jacobian is not provided, it is still helpful to provide the sparse
* Jacobian structure for the residuals through "KN_set_cb_rsd_jac()" to improve the
* efficiency of the finite-difference Jacobian approximation. Other optional
* information can also be set via "KN_set_cb_*() functions as detailed below.
*
* Returns 0 if OK, nonzero if error.
*/
int KNITRO_API KN_add_lsq_eval_callback ( KN_context_ptr kc,
const KNINT nR,
const KNINT * const indexRsds,
KN_eval_callback * const rsdCallback,
CB_context_ptr * const cb);
/** This API function is used to set the residual Jacobian structure and also
* (optionally) a callback function to evaluate the residual Jacobian provided
* through this callback.
*
* cb - a callback structure created from a previous call to
* KN_add_lsq_eval_callback()
* nnzJ - number of nonzeroes in the sparse residual Jacobian
* computed through this callback; set to KN_DENSE_ROWMAJOR to
* provide the full Jacobian in row major order (i.e. ordered
* by rows/residuals), or KN_DENSE_COLMAJOR to provide the full
* Jacobian in column major order (i.e. ordered by columns/
* variables)
* jacIndexRsds - (length nnzJ) residual index (row) of each nonzero;
* set to NULL if nnzJ=KN_DENSE_ROWMAJOR/KN_DENSE_COLMAJOR or nnzJ=0
* jacIndexVars - (length nnzJ) variable index (column) of each nonzero;
* set to NULL if nnzJ=KN_DENSE_ROWMAJOR/KN_DENSE_COLMAJOR or nnzJ=0
* rsdJacCallback - a pointer to a function that evaluates any residual Jacobian
* parts involved in this callback; set to NULL if using a finite-
* difference Jacobian approximation (specified via KN_set_cb_gradopt())
*
* The user should generally always try to define the sparsity structure
* for the Jacobian ("nnzJ", "jacIndexRsds", "jacIndexVars"). Even when
* using a finite-difference approximation to compute the Jacobian, knowing the
* sparse structure of the Jacobian can allow Knitro to compute this
* finite-difference approximation faster. However, if the user is unable to
* provide this sparsity structure, then one can set "nnzJ" to KN_DENSE_ROWMAJOR or
* KN_DENSE_COLMAJOR and set "jacIndexRsds" and "jacIndexVars" to NULL.
*/
int KNITRO_API KN_set_cb_rsd_jac ( KN_context_ptr kc,
CB_context_ptr cb,
const KNLONG nnzJ, /* or KN_DENSE_* */
const KNINT * const jacIndexRsds,
const KNINT * const jacIndexVars,
KN_eval_callback * const rsdJacCallback); /* nullable *
There is currently no callback for the exact Hessian in the least-squares API. If you wish to provide a callback for the user-supplied exact Hessian, you must use the standard API.
After solving, the residuals and residual Jacobian can be retrieved through the API
functions KN_get_rsd_values() and KN_get_rsd_jacobian_values().
See Callable library API reference for more details.
C example
The following C example illustrates how to use the Knitro least squares interface.
/* A simple nonlinear least-squares problem with 6 residual functions:
*
* min ( x0*1.309^x1 - 2.138 )^2 + ( x0*1.471^x1 - 3.421 )^2
* + ( x0*1.49^x1 - 3.597 )^2 + ( x0*1.565^x1 - 4.34 )^2
* + ( x0*1.611^x1 - 4.882 )^2 + ( x0*1.68^x1-5.66 )^2
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "knitro.h"
int callbackEvalR (KN_context_ptr kc,
CB_context_ptr cb,
KN_eval_request_ptr const evalRequest,
KN_eval_result_ptr const evalResult,
void * const userParams)
{
const double *x;
double *rsd;
if (evalRequest->type != KN_RC_EVALR)
{
printf ("*** callbackEvalR incorrectly called with eval type %d\n",
evalRequest->type);
return( -1 );
}
x = evalRequest->x;
rsd = evalResult->rsd;
/** Evaluate nonlinear residual components */
rsd[0] = x[0] * pow(1.309, x[1]);
rsd[1] = x[0] * pow(1.471, x[1]);
rsd[2] = x[0] * pow(1.49, x[1]);
rsd[3] = x[0] * pow(1.565, x[1]);
rsd[4] = x[0] * pow(1.611, x[1]);
rsd[5] = x[0] * pow(1.68, x[1]);
return( 0 );
}
int callbackEvalRJ (KN_context_ptr kc,
CB_context_ptr cb,
KN_eval_request_ptr const evalRequest,
KN_eval_result_ptr const evalResult,
void * const userParams)
{
const double *x;
double *rsdJac;
if (evalRequest->type != KN_RC_EVALRJ)
{
printf ("*** callbackEvalRJ incorrectly called with eval type %d\n",
evalRequest->type);
return( -1 );
}
x = evalRequest->x;
rsdJac = evalResult->rsdJac;
/** Evaluate non-zero residual Jacobian elements (row major order). */
rsdJac[0] = pow(1.309, x[1]);
rsdJac[1] = x[0] * log(1.309) * pow(1.309, x[1]);
rsdJac[2] = pow(1.471, x[1]);
rsdJac[3] = x[0] * log(1.471) * pow(1.471, x[1]);
rsdJac[4] = pow(1.49, x[1]);
rsdJac[5] = x[0] * log(1.49) * pow(1.49, x[1]);
rsdJac[6] = pow(1.565, x[1]);
rsdJac[7] = x[0] * log(1.565) * pow(1.565, x[1]);
rsdJac[8] = pow(1.611, x[1]);
rsdJac[9] = x[0] * log(1.611) * pow(1.611, x[1]);
rsdJac[10] = pow(1.68, x[1]);
rsdJac[11] = x[0] * log(1.68) * pow(1.68, x[1]);
return( 0 );
}
int main (int argc, char *argv[])
{
/** Declare variables. */
KN_context *kc;
int i, error;
int n, m;
/** Used to set constants for residuals */
double constants[6] = {-2.138, -3.421, -3.597, -4.34, -4.882, -5.66};
/** Pointer to structure holding information for evaluation
* callbacks. */
CB_context *cb;
/** Solution information. */
int nRC, nStatus;
double x[2];
double obj;
/** Create a new Knitro solver instance. */
error = KN_new(&kc);
if (error) exit(-1);
if (kc == NULL)
{
printf ("Failed to find a valid license.\n");
return( -1 );
}
/** Add the variables/parameters.
* Note: Any unset lower bounds are assumed to be
* unbounded below and any unset upper bounds are
* assumed to be unbounded above. */
n = 2; /* # of variables/parameters */
error = KN_add_vars(kc, n, NULL);
if (error) exit(-1);
/** Add the residuals. */
m = 6; /* # of residuals */
error = KN_add_rsds(kc, m, NULL);
if (error) exit(-1);
/** Set the array of constants in the residuals */
error = KN_add_rsd_constants_all(kc, constants);
if (error) exit(-1);
/** Add a callback function "callbackEvalR" to evaluate the nonlinear
* residual components. Note that the constant terms are added
* separately above, and will not be included in the callback. */
error = KN_add_lsq_eval_callback_all (kc, callbackEvalR, &cb);
if (error) exit(-1);
/** Also add a callback function "callbackEvalRJ" to evaluate the
* Jacobian of the residuals. If not provided, Knitro will approximate
* the residual Jacobian using finite-differencing. However, we recommend
* providing callbacks to evaluate the exact Jacobian whenever
* possible as this can drastically improve the performance of Knitro.
* We specify the residual Jacobian in "dense" row major form for simplicity.
* However for models with many sparse residuals, it is important to specify
* the non-zero sparsity structure of the residual Jacobian for efficiency
* (this is true even when using finite-difference gradients). */
error = KN_set_cb_rsd_jac (kc, cb, KN_DENSE_ROWMAJOR, NULL, NULL, callbackEvalRJ);
if (error) exit(-1);
/** Solve the problem.
*
* Return status codes are defined in "knitro.h" and described
* in the Knitro manual.
*/
nRC = KN_solve (kc);
/** Delete the knitro solver instance. */
KN_free (&kc);
return( 0 );
}