Callbacks
Knitro needs to evaluate the objective function and constraints (function values and ideally, their derivatives) at various points along the optimization process. If these functions are linear or quadratic then Knitro has specialized API routines for loading their linear and quadratic structures. However, in order to pass this information to Knitro for more general nonlinear functions, you need to provide a handle to a user-defined function that performs the necessary computation. This is referred to as a callback.
Callbacks in Knitro require you to supply several function pointers that Knitro calls when it needs new function, gradient or Hessian values for nonlinear functions (as well as for other specialized user non-evaluation callbacks decribed below or in Callable library API reference).
If your callback requires additional parameters beyond what is passed through the arguments, you are encouraged to create a structure containing them and pass its address as the userParams pointer. Knitro does not modify or dereference the userParams pointer, so it is safe to use for this purpose.
The C language prototypes for the Knitro callback functions
are defined in knitro.h. The prototype used for evaluation callbacks is:
/** Function prototype for evaluation callbacks. */
typedef int KN_eval_callback (KN_context_ptr kc,
CB_context_ptr cb,
KN_eval_request_ptr const evalRequest,
KN_eval_result_ptr const evalResult,
void * const userParams);
where the structures used to define the arguments evalRequest and evalResult
are given by:
/** Structure used to pass back evaluation information for evaluation callbacks.
*
* type: - indicates the type of evaluation requested
* threadID: - the thread ID associated with this evaluation request;
* useful for multi-threaded, concurrent evaluations
* x: - values of unknown (primal) variables used for all evaluations
* lambda: - values of unknown dual variables/Lagrange multipliers
* used for the evaluation of the Hessian
* sigma: - scalar multiplier for the objective component of the Hessian
* vec: - vector array value for Hessian-vector products (only used
* when user option hessopt=KN_HESSOPT_PRODUCT)
*/
typedef struct KN_eval_request {
int type;
int threadID;
const double * x;
const double * lambda;
const double * sigma;
const double * vec;
} KN_eval_request, *KN_eval_request_ptr;
/** Structure used to return results information for evaluation callbacks.
* The arrays (and their indices and sizes) returned in this structure are
* local to the specific callback structure used for the evaluation.
*
* obj: - objective function evaluated at "x" for EVALFC or
* EVALFCGA request (funcCallback)
* c: - (length nC) constraint values evaluated at "x" for
* EVALFC or EVALFCGA request (funcCallback)
* objGrad: - (length nV) objective gradient evaluated at "x" for
* EVALGA request (gradCallback) or EVALFCGA request (funcCallback)
* jac: - (length nnzJ) constraint Jacobian evaluated at "x" for
* EVALGA request (gradCallback) or EVALFCGA request (funcCallback)
* hess: - (length nnzH) Hessian evaluated at "x", "lambda", "sigma"
* for EVALH or EVALH_NO_F request (hessCallback)
* hessVec: - (length n=number variables in the model) Hessian-vector
* product evaluated at "x", "lambda", "sigma"
* for EVALHV or EVALHV_NO_F request (hessCallback)
* rsd: - (length nR) residual values evaluated at "x" for EVALR
* request (rsdCallback)
* rsdJac: - (length nnzJ) residual Jacobian evaluated at "x" for
* EVALRJ request (rsdJacCallback)
*/
typedef struct KN_eval_result {
double * obj;
double * c;
double * objGrad;
double * jac;
double * hess;
double * hessVec;
double * rsd;
double * rsdJac;
} KN_eval_result, *KN_eval_result_ptr;
The callback functions for evaluating the functions, gradients and Hessian are set as described below. Each user callback routine should return an int value of 0 if successful, or a negative value to indicate that an error occurred during execution of the user-provided function. See the Derivatives section for details on how to compute the Jacobian and Hessian matrices in a form suitable for Knitro.
Minimally, and as a first step, you must call KN_add_eval_callback()
to establish a callback to evaluate the nonlinear functions in your model.
/** This is the routine for adding a callback for (nonlinear) evaluations
* of objective and constraint functions. This routine can be called
* multiple times to add more than one callback structure (e.g. to create
* different callback structures to handle different blocks of constraints).
* This routine specifies the minimal information needed for a callback, and
* creates the callback structure "cb", which can then be passed to other
* callback functions to set additional information for that callback.
*
* evalObj - boolean indicating whether or not any part of the objective
* function is evaluated in the callback
* nC - number of constraints evaluated in the callback
* indexCons - (length nC) index of constraints evaluated in the callback
* (set to NULL if nC=0)
* funcCallback - a pointer to a function that evaluates the objective parts
* (if evalObj=KNTRUE) and any constraint parts (specified by
* nC and indexCons) involved in this callback; when
* eval_fcga=KN_EVAL_FCGA_YES, this callback should also evaluate
* the relevant first derivatives/gradients
* cb - (output) the callback structure that gets created by
* calling this function; all the memory for this structure is
* handled by Knitro
*
* After a callback is created by "KN_add_eval_callback()", the user can then specify
* gradient information and structure through "KN_set_cb_grad()" and Hessian
* information and structure through "KN_set_cb_hess()". If not set, Knitro will
* approximate these. However, it is highly recommended to provide a callback routine
* to specify the gradients if at all possible as this will greatly improve the
* performance of Knitro. Even if a gradient callback is not provided, it is still
* helpful to provide the sparse Jacobian structure through "KN_set_cb_grad()" to
* improve the efficiency of the finite-difference gradient approximations.
* Other optional information can also be set via "KN_set_cb_*() functions as
* detailed below.
*
* Returns 0 if OK, nonzero if error.
*/
int KNITRO_API KN_add_eval_callback ( KN_context_ptr kc,
const KNBOOL evalObj,
const KNINT nC,
const KNINT * const indexCons, /* nullable if nC=0 */
KN_eval_callback * const funcCallback,
CB_context_ptr * const cb);
This callback returns a callback structure cb that can then be passed to other
callback evaluation routines to specify particular, optional, properties
for that callback. For example, it can be passed to KN_set_cb_grad()
to specify a callback function for gradients (i.e. first derivatives) or
KN_set_cb_hess() to specify a callback for the Hessian. If these
are not set, Knitro will approximate derivatives internally. However, we
highly recommend providing callbacks to evaluate derivatives whenever possible
as this can dramatically improve the performance of Knitro.
Although the easiest approach is to create one callback structure
to use for all evaluations, it is possible to call KN_add_eval_callback()
multiple times to create different cb callback structures for different groups of
nonlinear functions. This would allow, for instance, providing exact derivatives
for some functions via callbacks, while having Knitro approximate other
derivatives using finite-differencing.
For least-squares problems use KN_add_lsq_eval_callback() and
KN_set_cb_rsd_jac(). See Nonlinear Least-Squares for more details.
Other evaluation callback API functions include KN_set_cb_user_params(),
KN_set_cb_gradopt(), and KN_set_cb_relstepsizes(). More may
be added in the future.
These are described in detail in Callable library API reference.
Knitro also provides a special callback function for output printing.
By default Knitro prints to stdout or a knitro.log file,
as determined by the outmode option.
Alternatively, you can define a callback function to handle
all output. This callback function can be set as shown below
int KNITRO_API KN_set_puts_callback (KN_context_ptr kc,
KN_puts * const fnPtr,
void * const userParams);
The prototype for the Knitro callback function used for handling output is
typedef int KN_puts (const char * const str,
void * const userParams);
In addition to the callbacks defined above, Knitro makes additional callbacks
available to the user for features such as multi-start and MINLP, including
KN_set_newpt_callback(),
KN_set_mip_node_callback(), and
KN_set_ms_initpt_callback().
The prototype used for many of the other non-evaluation user callbacks (e.g. the newpoint callback) is:
/** Type declaration for several non-evaluation user callbacks defined
* below.
*/
typedef int KN_user_callback ( KN_context_ptr kc,
const double * const x,
const double * const lambda,
void * const userParams);
Please see a complete list and description of Knitro callback functions in
the Callable library API reference section in the Reference Manual.
In addition, we recommend
closely reviewing the examples provided in examples/C which provide
examples of how to use most of these callback functions.
For information on setting callbacks in the object-oriented interface, see the Object-oriented interface reference.
Example
Consider the following nonlinear optimization problem from the Hock and Schittkowski test set.
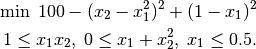
This problem is coded as examples/C/exampleNLP1.c.
Note
The Knitro distribution comes with several C language programs in
the directory examples/C. The instructions in
examples/C/README.txt explain how to compile and run the examples.
This section overviews the coding of driver programs using the callback interface,
but the working examples provide more complete detail.
Every driver starts by allocating a new Knitro solver instance
and checking that it succeeded (KN_new() might return NULL
if the Artelys license check fails):
#include "knitro.h"
/*... Include other headers, define main() ...*/
KN_context *kc;
/*... Declare other local variables ...*/
double xLoBnds[2] = {-KN_INFINITY, -KN_INFINITY};
double xUpBnds[2] = {0.5, KN_INFINITY};
double xInitVals[2] = {-2.0, 1.0};
double cLoBnds[2] = {1.0, 0.0};
error = KN_new(&kc);
if (error) exit(-1);
if (kc == NULL)
{
printf ("Failed to find a valid license.\n");
return( -1 );
}
The next task is to load the problem definition into the solver using various API functions for adding variables and constraints, bounds, linear and quadratic structures, etc. The code below captures the basic problem definition passed to Knitro:
/** Initialize Knitro with the problem definition. */
/** Add the variables and set their bounds.
* Note: any unset lower bounds are assumed to be
* unbounded below and any unset upper bounds are
* assumed to be unbounded above. */
n = 2;
error = KN_add_vars(kc, n, NULL);
if (error) exit(-1);
error = KN_set_var_lobnds_all(kc, xLoBnds); /* not necessary since infinite */
if (error) exit(-1);
error = KN_set_var_upbnds_all(kc, xUpBnds);
if (error) exit(-1);
/** Define an initial point. If not set, Knitro will generate one. */
error = KN_set_var_primal_init_values_all(kc, xInitVals);
if (error) exit(-1);
/** Add the constraints and set their lower bounds */
m = 2;
error = KN_add_cons(kc, m, NULL);
if (error) exit(-1);
error = KN_set_con_lobnds_all(kc, cLoBnds);
if (error) exit(-1);
/** Both constraints are quadratic so we can directly load all the
* structure for these constraints. */
/** First load quadratic structure x0*x1 for the first constraint */
indexVar1 = 0; indexVar2 = 1; coef = 1.0;
error = KN_add_con_quadratic_struct_one (kc, 1, 0,
&indexVar1, &indexVar2, &coef);
if (error) exit(-1);
/** Load structure for the second constraint. below we add the linear
* structure and the quadratic structure separately, though it
* is possible to add both together in one call to
* "KN_add_con_quadratic_struct_one()" since this api function also
* supports adding linear terms. */
/** Add linear term x0 in the second constraint */
indexVar1 = 0; coef = 1.0;
error = KN_add_con_linear_struct_one (kc, 1, 1,
&indexVar1, &coef);
if (error) exit(-1);
/** Add quadratic term x1^2 in the second constraint */
indexVar1 = 1; indexVar2 = 1; coef = 1.0;
KN_add_con_quadratic_struct_one (kc, 1, 1,
&indexVar1, &indexVar2, &coef);
After loading the basic problem information, we add the callbacks for evaluating the nonlinear objective function (and it’s derivatives) as shown below.
/** Add a callback function "callbackEvalF" to evaluate the nonlinear
* (non-quadratic) objective. Note that the linear and
* quadratic terms in the objective could be loaded separately
* via "KN_add_obj_linear_struct()" / "KN_add_obj_quadratic_struct()".
* However, for simplicity, we evaluate the whole objective
* function through the callback. */
error = KN_add_eval_callback (kc, KNTRUE, 0, NULL, callbackEvalF, &cb);
if (error) exit(-1);
/** Also add a callback function "callbackEvalG" to evaluate the
* objective gradient. If not provided, Knitro will approximate
* the gradient using finite-differencing. However, we recommend
* providing callbacks to evaluate the exact gradients whenever
* possible as this can drastically improve the performance of Knitro.
* We specify the objective gradient in "dense" form for simplicity.
* However for models with many constraints, it is important to specify
* the non-zero sparsity structure of the constraint gradients
* (i.e. Jacobian matrix) for efficiency (this is true even when using
* finite-difference gradients). */
error = KN_set_cb_grad (kc, cb, KN_DENSE, NULL, 0, NULL, NULL, callbackEvalG);
if (error) exit(-1);
/** Add a callback function "callbackEvalH" to evaluate the Hessian
* (i.e. second derivative matrix) of the objective. If not specified,
* Knitro will approximate the Hessian. However, providing a callback
* for the exact Hessian (as well as the non-zero sparsity structure)
* can greatly improve Knitro performance and is recommended if possible.
* Since the Hessian is symmetric, only the upper triangle is provided.
* Again for simplicity, we specify it in dense (row major) form. */
error = KN_set_cb_hess (kc, cb, KN_DENSE_ROWMAJOR, NULL, NULL, callbackEvalH);
if (error) exit(-1);
These evaluation callback functions use the KN_eval_callback() prototype.
In examples/C/exampleNLP1.c these are named
callbackEvalF, callbackEvalG, and callbackEvalH.
/*------------------------------------------------------------------*/
/* FUNCTION callbackEvalF */
/*------------------------------------------------------------------*/
/** The signature of this function matches KN_eval_callback in knitro.h.
* Only "obj" is set in the KN_eval_result structure.
*/
int callbackEvalF (KN_context_ptr kc,
CB_context_ptr cb,
KN_eval_request_ptr const evalRequest,
KN_eval_result_ptr const evalResult,
void * const userParams)
{
const double *x;
double *obj;
double dTmp;
if (evalRequest->type != KN_RC_EVALFC)
{
printf ("*** callbackEvalFC incorrectly called with eval type %d\n",
evalRequest->type);
return( -1 );
}
x = evalRequest->x;
obj = evalResult->obj;
/** Evaluate nonlinear objective */
dTmp = x[1] - x[0]*x[0];
*obj = 100.0 * (dTmp*dTmp) + ((1.0 - x[0])*(1.0 - x[0]));
return( 0 );
}
/*------------------------------------------------------------------*/
/* FUNCTION callbackEvalG */
/*------------------------------------------------------------------*/
/** The signature of this function matches KN_eval_callback in knitro.h.
* Only "objGrad" is set in the KN_eval_result structure.
*/
int callbackEvalG (KN_context_ptr kc,
CB_context_ptr cb,
KN_eval_request_ptr const evalRequest,
KN_eval_result_ptr const evalResult,
void * const userParams)
{
const double *x;
double *objGrad;
double dTmp;
if (evalRequest->type != KN_RC_EVALGA)
{
printf ("*** callbackEvalGA incorrectly called with eval type %d\n",
evalRequest->type);
return( -1 );
}
x = evalRequest->x;
objGrad = evalResult->objGrad;
/** Evaluate gradient of nonlinear objective */
dTmp = x[1] - x[0]*x[0];
objGrad[0] = (-400.0 * dTmp * x[0]) - (2.0 * (1.0 - x[0]));
objGrad[1] = 200.0 * dTmp;
return( 0 );
}
/*------------------------------------------------------------------*/
/* FUNCTION callbackEvalH */
/*------------------------------------------------------------------*/
/** The signature of this function matches KN_eval_callback in knitro.h.
* Only "hess" and "hessVec" are set in the KN_eval_result structure.
*/
int callbackEvalH (KN_context_ptr kc,
CB_context_ptr cb,
KN_eval_request_ptr const evalRequest,
KN_eval_result_ptr const evalResult,
void * const userParams)
{
const double *x;
double sigma;
double *hess;
if ( evalRequest->type != KN_RC_EVALH
&& evalRequest->type != KN_RC_EVALH_NO_F)
{
printf ("*** callbackEvalHess incorrectly called with eval type %d\n",
evalRequest->type);
return( -1 );
}
x = evalRequest->x;
/** Scale objective component of hessian by sigma */
sigma = *(evalRequest->sigma);
hess = evalResult->hess;
/** Evaluate the hessian of the nonlinear objective.
* Note: Since the Hessian is symmetric, we only provide the
* nonzero elements in the upper triangle (plus diagonal).
* These are provided in row major ordering as specified
* by the setting KN_DENSE_ROWMAJOR in "KN_set_cb_hess()".
* Note: The Hessian terms for the quadratic constraints
* will be added internally by Knitro to form
* the full Hessian of the Lagrangian. */
hess[0] = sigma * ( (-400.0 * x[1]) + (1200.0 * x[0]*x[0]) + 2.0); // (0,0)
hess[1] = sigma * (-400.0 * x[0]); // (0,1)
hess[2] = sigma * 200.0; // (1,1)
return( 0 );
}
Back in the main program KN_solve() is invoked to find the solution:
/** Solve the problem.
*
* Return status codes are defined in "knitro.h" and described
* in the Knitro manual.
*/
nStatus = KN_solve (kc);
/** Delete the Knitro solver instance. */
KN_free (&kc);