| KAbs |
This class creates a X = abs(Y) constraint
Example :
|
| KAbs.PropagationLevel |
Propagation level of the constraint
|
| KAbsoluteToleranceOptimalityChecker |
An OptimalityToleranceChecker to use with any type of
KNumVar objective, which use an absolute difference criteria.
|
| KACBinConstraint |
This class implements a generic class for propagation of any binary constraint by local 2-consistency (arc consistency) \
Two algorithms (AC3 and AC2001) are available for propagation of the constraint.
Example : X == Y + C
|
| KACBinConstraint.acAlgorithms |
Differents level of propagation for the constraints
|
| KACBinTableConstraint |
This class implements a generic class for propagation of any binary constraint by local 2-consistency (arc consistency).
Two algorithms (AC3 and AC2001) are available for propagation of the constraint.
|
| KACBinTableConstraint.acAlgorithms |
Arc-consistency algorithms for binary table constraint
|
| KAllDifferent |
This class creates a X1 <> X2 <> ...
|
| KAllDifferent.PropagationLevel |
Differents level of propagation for the constraints
|
| KAssignAndForbid |
Assign And Forbid branching scheme
Example :
|
| KAssignVar |
AssignVar Branching scheme
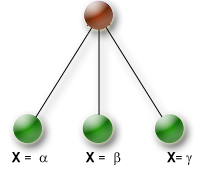
Example: |
| KAuxVar |
This class represents an auxiliary variable to use in relaxations.
KAuxVar objects represent auxiliary variables, consisting of a name, lower
and upper bounds, and a type that is either "global" or "continuous".
|
| KBestBoundValue |
Value selector that selects the value of a variable that implies the best
bound for the objective.
For each possible value in the domain of a given variable, the variable
is instantiated on this value and the propagation is launched.
|
| KBiLevelLinearRelaxationSolverConfigurator |
|
| KBinTerm |
This class represent an expression of the form X (+ , -) Y + cste where X and
Y are variables and cste an integer constant.
|
| KBranchingScheme |
Abstract class defining branching schemes.
Search is made thanks to a tree search algorithm.
|
| KBranchingSchemeArray |
This class implements an array of KBranchingScheme
Example :
|
| KBranchingSchemeGroup |
A branching scheme group represents a list of branching schemes to use nested
branching schemes.
|
| KBranchingSchemeGroupArray |
List of brancing scheme group.
|
| KBranchingSchemeGroupSelector |
Selection object to choose among a list of branching scheme group.
|
| KBranchingSchemeGroupSerializer |
A nested branching scheme.
From a list of branching scheme groups, this brancing scheme apply
iteratively each group.
The default group selector uses input order.
|
| KClpLinearRelaxationSolver |
Linear relaxation solver for Clp
|
| KCoinLinearRelaxationSolver |
This linear relaxation solver relies on CoinMP to solve the LP/MIP problem.
Example:
|
| KConditionNumLinComb |
Conditionnal numeric linear combination constraint.
This constraint can be represented as a linear combination
Sum(a_i * X_i * f(X_i)) { <= , != , == } C where the function f(X_i) is an
indicator (1 or 0) function to specify.
|
| KConditionNumLinComb.LinCombOperator |
Available operators for the combination
|
| KConjunction |
This class creates a Binary conjunction on two constraints `C1 and C2`.
Example :
|
| KConstraint |
This class is an abstract interface for all constraints in Artelys Kalis
|
| KConstraintArray |
This class implements an array of KConstraint
Example :
|
| KCopiableRelaxationSolverConfigurator |
|
| KCumulativeResourceConstraint |
This constraint states that some tasks requiring a resource do not exceed the
resource capacity.
|
| KCumulativeResourceConstraintResourceUsage |
A time-dependant resource usage constraint.
|
| KCycle |
The cycle constraint ensures that the graph implicitly represented by a set of variables and their domain contains no sub-tours (tour visiting a partial number of nodes).
|
| KDiscreteResource |
Discrete resource
A discrete resource can process several tasks at the same time.
The following schema shows an example with three tasks A,B and C executing on
a disjunctive resource and on a cumulative resource with resource usage 3 for
task A, 1 for task B and 1 for task C :
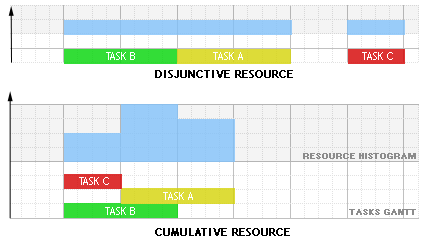
Tasks may require, provide, consume and produce resources :
- A task requires a resource if some amount of the resource capacity must be made available for the execution of the activity. |
| KDiscreteResource.PropagationHint |
Propagation Hint Attributes
|
| KDisjunction |
This class creates a Binary disjunction on two constraints `C1 or C2`
Example :
|
| KDisjunctionArray |
This class implements an array of KDisjunction
Example :
|
| KDisjunctionInputOrder |
This class implements a disjunction selector that selects the disjunction in the input order.
|
| KDisjunctionPriorityOrder |
This class implements a disjunction selector that selects first the disjunction ith the highest priority
Example :
|
| KDisjunctionSelector |
Abstract interface class for disjunction selection heuristic
|
| KDistanceEqualXyc |
This class creates a abs(X-Y) == C constraint
Example :
|
| KDistanceGreaterThanXyc |
This class creates a abs(X-Y) >= C constraint
Example :
|
| KDistanceLowerThanXyc |
This class creates a abs(X-Y) <= C constraint
Example :
|
| KDistanceNotEqualXyc |
This class creates a abs(X-Y) != C constraint
Example :
|
| KDoubleAnnotation |
|
| KDoubleArray |
This class implements an array of doubles
Example :
|
| KElement |
This class creates a x == tab[i + cste] constraint
Example :
|
| KElement2D |
This class creates a X == Tab[I + cste1][J + cste2] constraint
Example :
|
| KEltTerm |
This class represent an expression of type Tab[I] where Tab is an array of integer value and I is the indexing variable
Example :
|
| KEltTerm2D |
This class represent an expression of type Tab[I+a][J+b] where Tab is an array of integer value; I,J are the indexing variable and a and b indexing offsets
Example :
|
| KEqualXc |
This class creates a X == C constraint.
Example :
|
| KEqualXyc |
This class creates a X == Y + C constraint.
Example :
|
| KEquiv |
This class creates an Equivalence on two constraints `C1 <==> C2`.
Example :
|
| KFinishedMessage |
|
| KFloatVar |
This class implements a variable with continuous real valued domain.
Conceptually the continuous variables can be represented the following way :
Example:
|
| KFloatVar.PrecisionRelativity |
|
| KFloatVarBranchingScheme |
This branching scheme is suited for branching on KFloatVar objects.
|
| KFloatVarSelector |
Float variable selector
|
| KGeneralizedArcConsistencyConstraint |
This class implements a generic class for propagation of any nary constraint by forward checking/arc consistency or generalized arc consistency
|
| KGeneralizedArcConsistencyConstraint.acAlgorithms |
Possible propagation algorithms
|
| KGeneralizedArcConsistencyTableConstraint |
This class implements a generic class for propagation of any n-ary constraint by generalized arc consistency \
|
| KGlobalCardinalityConstraint |
This class implements a Global Cardinality Constraint.
A GCC (Global Cardinality Constraint) over a set of variables is defined by three arrays called
values,
lowerBound, and upperBound.
|
| KGreaterOrEqualXc |
This class creates a X >= C constraint.
Example :
|
| KGreaterOrEqualXyc |
This class creates a X >= Y + C constraint
Example :
|
| KGuard |
This class creates an implication on two constraints `C1 ==> C2`
Example :
|
| KHybridSolution |
This class represents a solution of a relaxation solver, that is, a mapping
from variables (KNumVar and/or KAuxVar) to their value.
Example :
|
| KInputOrder |
This class implements a variable selector that selects the first uninstantiated variable in the input order.
Example :
|
| KIntAnnotation |
|
| KIntArray |
This class implements an array of integers
Example :
|
| KIntegerObjectiveOptimalityChecker |
An OptimalityToleranceChecker to use with integer objective only.
|
| KIntervalDomain |
Branching scheme for splitting float variables into a set of intervals.
This branching scheme split the domain of a float variable into interval
of length `gap`.
|
| KIntMatrix |
This class implements an matrix of integers
|
| KIntSetIntAnnotation |
|
| KIntVar |
This class implements an integer variable with enumerated (finite) domain.
Decision variables are the variable quantities that we are trying to
instantiate in order to satisfy the constraints of our problem.
In this version, Artelys Kalis works with integer variables : decision
variables which are constrained to take only integer values.
These integer variables are represented by instances of the class KIntVar.
Example :
|
| KIntVarArray |
This class implements an array of KIntVar with enumerated (finite) domains
Example :
|
| KIntVarBranchingScheme |
Abstract class for Branching scheme.
|
| KIntVarMatrix |
This class implements an matrix of KIntVar
Example :
|
| KLargestDomain |
This class implements a variable selector that selects the first uninstantiated variable with the smallest domain.
Example :
|
| KLargestDurationDomain |
Largest domain duration task selection heuristic
|
| KLargestEarliestCompletionTime |
Largest Earliest Completion time task selection heuristic
|
| KLargestEarliestStartTime |
Largest Earliest Start time task selection heuristic
|
| KLargestLatestCompletionTime |
Largest Latest Completion time task selection heuristic
|
| KLargestLatestStartTime |
Largest Latest Start time task selection heuristic
|
| KLargestMax |
This class implements a variable selector that selects first the variable
with the largest upperbound in its domain.
Example:
|
| KLargestMin |
This class implements a variable selector that selects first the variable
with the largest lower bound.
Example:
|
| KLargestReducedCost |
This variable selector selects the variable with biggest reduced cost in current LP solution
of the provided linear relaxation solver.
Note that it does NOT call the solve() method of the solver automatically.
The current LP solution is simply read as it is.
|
| KLessOrEqualXc |
This class creates a X <= C constraint.
|
| KLinComb |
This class creates a Sum(ai.Xi) { <= , != , == } C constraint
Example :
|
| KLinComb.LinCombOperator |
|
| KLinearRelaxation |
This class represents a linear relaxation of a domain.
A linear relaxation consists of the following.
- A set of involved variables
- A type for each variable (either continuous or global).
|
| KLinearRelaxationSolver |
This class is intended as a superclass for linear relaxation solvers.
Such a solver must be provided with
- a linear relaxation (KLinearRelaxation)
- an objective variable (KNumVar)
- a sense for optimization (KProblem::Sense).
It relies on a LP/MIP solver to provide the following information:
- a value (a bound for the relaxed problem, cf method getBound())
- a solution, possibly not feasible for the original problem, but which can be used to guide the search for a feasible solution
- if the problem is LP, reduced costs (that can be used for instance in the "reduced cost fixing" procedure).
|
| KLinearRelaxationSolver.SolveAlgorithm |
Resolution algorithms
|
| KLinearRelaxationSolverConfigurator |
|
| KLinRel |
This class represents a linear relation (equality or inequality) between variables.
Variables involved in the KLinRel object can be a mix of KNumVar and KAuxVar.
|
| KLinTerm |
This class represent a linear term of the form Sum(coeffs[i].lvars[i]) + cst
Example :
|
| KMax |
This class creates a vMax = max(X1,X2,...,Xn) constraint
Example :
|
| KMaxDegree |
This class implements a variable selector that selects first the variable
involved in the maximum number of constraints.
Example :
|
| KMaxRegretOnLowerBound |
This class implements a variable selector that selects first the variable with maximum regret on its lowerbound.
Example :
|
| KMaxRegretOnUpperBound |
This class implements a variable selector that selects first the variable
with maximum regret on its upperbound.
Example :
|
| KMaxToMin |
This class implements a value selector that returns values in decreasing
order.
Example :
|
| KMessage |
|
| KMessageBox |
|
| KMiddle |
This class implements a value selector that selects the nearest value from
the middle value in the domain of the variable.
Example :
|
| KMin |
This class creates a vMin = min(X1,X2,...,Xn) constraint
Example :
|
| KMinMaxConflict |
Value selector that selects the value of a variable that implies the best
problem size reduction when instantiated.
For each possible value of the domain of the variable, the variable is
instantiated and the problem size reduction is evaluated.
|
| KMinToMax |
This class implements a value selector that returns values in increasing
order.
Example :
|
| KMostFractional |
This variable selector selects the variable with biggest fractional part in
the current solution held by the provided linear relaxation solver.
Note that it does NOT call the "solve" method of the solver, so if you want
the relaxation to be re-solved at each node, you must use method
KSolver::setOtherNodesRelaxationSolver.
|
| KNearestNeighbor |
A nearest neighboor branching scheme based on a distance matrix.
|
| KNearestRelaxedValue |
This value selector chooses the value closest to the relaxed solution
contained in the provided solver.
|
| KNearestValue |
This class implements a value selector that selects the nearest value from
target in the domain of the variable.
Example :
|
| KNonLinearTerm |
This class represent a non linear term.
Example :
|
| KNonLinearTerm.AlgebricOperator |
|
| KNonLinearTerm.CompareOperator |
|
| KNonLinearTerm.NonLinFunction |
|
| KNotEqualXc |
This class creates a X != C constraint
Example :
|
| KNotEqualXyc |
This class creates a X <> Y + C constraint
Example :
|
| KNumAnnotation |
|
| KNumDistanceEqualXyc |
This class creates a abs(X-Y) == C constraint
Example :
|
| KNumDistanceGreaterThanXyc |
This class creates a `abs(X-Y) >= C` constraint
Example :
|
| KNumDistanceLowerThanXyc |
This class creates a `abs(X-Y) <= C` constraint
Example :
|
| KNumEqualXc |
This class creates a `X == C` constraint
Example :
|
| KNumEqualXYc |
This class creates a `X == Y + C` constraint
Example :
|
| KNumEqualXYZ |
This class creates a `X == Y + Z` constraint
Example :
|
| KNumGreaterOrEqualXc |
This class creates a `X >= C` constraint
Example :
|
| KNumGreaterOrEqualXyc |
This class creates a `X >= Y + C` constraint
Example :
|
| KNumInputOrder |
This class implements a variable selector that selects the first uninstantiated variable in the input order.
Example :
|
| KNumLargestReducedCost |
This variable selector selects the variable with biggest reduced cost in
current LP solution of the provided linear relaxation solver.
|
| KNumLessOrEqualXc |
This class creates a `X <= C` constraint
Example :
|
| KNumLinComb |
This class creates a Sum(ai.Xi) { <= , != , == } C constraint
Example :
|
| KNumLinComb.LinCombOperator |
|
| KNumLowerOrEqualXyc |
This class creates a `X <= Y + C` constraint
Example :
|
| KNumMiddle |
This class implements a value selector that selects the nearest value from
the middle value in the domain of the variable.
Example :
|
| KNumNearestRelaxedValue |
This value selector chooses the value closest to the relaxed solution
contained in the provided solver.
If the relaxed value for a KFloatVar variable is within its bounds, the
selected value is simply the relaxed value.
|
| KNumNearestValue |
This class implements a value selector that selects the nearest value from target in the domain of the variable .
Example :
|
| KNumNonLinearComb |
This class represents a constraint to propagate any non linear constraint of
the form KNonLinearTerm COMPARATOR KNonLinearTerm.
|
| KNumNonLinearComb.NonLinearCombOperator |
Available operators for the constraint
|
| KNumObjectiveOptimalityChecker |
An OptimalityToleranceChecker to use with any type of
KNumVar objective, which use both a relative and absolute
difference criteria.
|
| KNumSmallestDomain |
Smallest domain variable selector
|
| KNumValueSelector |
Abstract interface class for value selection heuristic
|
| KNumVar |
Superclass of decision variables
|
| KNumVar.Type |
Variable types
|
| KNumVarArray |
This class implements an array of KNumVar.
Example :
|
| KNumVariableSelector |
Abstract interface class for variable selection heuristic.
|
| KNumXEqualsAbsY |
This class creates a `X = |Y|` constraint
Example :
|
| KNumXEqualsAtan2YZ |
This class creates a X = atan2(Y, Z) constraint.
Atan2(Y, Z) is defined as follow :
- atan(Y/Z) if Z > 0
- atan(Y/Z) + PI if Z < 0 and Y >= 0
- atan(Y/Z) - PI if Z < 0 and Y < 0
- (+ PI / 2) if Z = 0 and Y > 0
- (- PI / 2) if Z = 0 and Y < 0
- undefined if Z = 0 and Y = 0
Domain of X variable is at least (-PI, PI].
Example :
|
| KNumXEqualsLnY |
This class creates a X = ln(Y) constraint
Example :
|
| KNumXEqualsYArithPowC |
This class creates a X = Y ^ C constraint
Example :
|
| KNumXEqualsYSquared |
This class creates a `X = Y^2` constraint
Example :
|
| KNumXEqualsYTimesC |
This class creates a `X = Y * C` constraint
Example :
|
| KNumXEqualsYTimesZ |
This class creates a `X == Y * Z` constraint
Example :
|
| KNumXOperatorACosY |
This class creates a X {==,<=,>=} acos(Y) constraint
Example :
|
| KNumXOperatorASinY |
This class creates a X {==,<=,>=} asin(Y) constraint
Example :
|
| KNumXOperatorATanY |
This class creates a X {==,<=,>=} atan(Y) constraint
Example :
|
| KNumXOperatorCosY |
This class creates a X {==,<=,>=} cos(Y) constraint
Example :
|
| KNumXOperatorExpY |
This class creates a X {==,<=,>=} exp(Y) constraint
Example :
|
| KNumXOperatorLnY |
This class creates a X {==,<=,>=} ln(Y) constraint
Example :
|
| KNumXOperatorSinY |
This class creates a X {==,<=,>=} sin(Y) constraint
Example :
|
| KNumXOperatorTanY |
This class creates a X {==,<=,>=} tan(Y) constraint
Example :
|
| KOccurrence |
This class creates an occurence constraint of a value in a list of variables
Example :
|
| KOccurTerm |
This class represent an expression of type occur(target,lvars) where target
is the value for wich we want to restrict the number of occurence(s) in the
lVars array of variables.
Example :
|
| KOptimalityToleranceChecker |
This interface sets a framework for objects providing method to check if the
current solution is close enough to the optimum, and, if not, to give a new
bound to set on the objective variable.
|
| KOptimizeListener |
|
| KOptimizeWithISListener |
|
| KOtherNodeLinearRelaxationSolverConfigurator |
|
| KParallelBranchingScheme |
Parallel branching scheme
Example:
|
| KParallelSolverEventListener |
|
| KPathOrder |
A variable selector based on a path order.
The initial successor is chosen randomly.
|
| KProbe |
Probe branching scheme
|
| KProbeDisjunction |
ProbeDisjunction branching scheme
|
| KProblem |
Constraint satisfaction and optimization problems include variables,
constraints ( modeling entities ) and might have solutions after search.
Such problems are represented in Artelys Kalis by objects of the class
KProblem.
|
| KProblem.constraintClass |
Constraint classes for which an automatic relaxation is available
|
| KProblem.LogLevel |
Ouput log level
|
| KProblem.Sense |
Sense for optimization
|
| KRandomValue |
This class implements a value selector that selects a value at random in the domain of the variable.
Example :
|
| KRandomVariable |
This class implements a variable selector that selects an uninstantiated
variable at random.
Example :
|
| KRelation |
A relation term between an expression and constants.
|
| KRelation.Comparator |
|
| KRelativeToleranceOptimalityChecker |
An OptimalityToleranceChecker to use with any type of
KNumVar objective, which use a relative difference criteria.
|
| KRelaxationSolver |
This class is intended as a superclass for linear relaxation solvers.
Such a solver must be provided with
- a linear relaxation (KLinearRelaxation)
- an objective variable (KNumVar)
- a sense for optimization (KProblem::Sense).
It relies on a LP/MIP solver to provide the following information:
- a value (a bound for the relaxed problem, cf method getBound())
- a solution, possibly not feasible for the original problem, but which can be used to guide the search for a feasible solution
- if the problem is LP, reduced costs (that can be used for instance in the "reduced cost fixing" procedure).
|
| KRelaxationSolverConfigurator |
|
| KResource |
Resources (machines, raw material etc) can be of two different types :
- Disjunctive when the resource can process only one task at a time (represented by the class KUnaryResource).
- Cumulative when the resource can process several tasks at the same time (represented by the class KDiscreteResource).
Traditional examples of disjunctive resources are Jobshop problems,
cumulative resources are heavily used for the Resource-Constrained Project
Scheduling Problem (RCPSP).
|
| KResourceArray |
This class implements an array of KResource
Example :
|
| KResourceSelector |
Resource selection heuristic
|
| KResourceUsage |
A KResourceUsage object can be used to describe the a specific usage of a
given resource.
|
| KResourceUsageArray |
Utility container for storing a list of KResourceUsage
|
| KSchedule |
Scheduling and planning problems are concerned with determining a plan for
the execution of a given set of tasks.
The objective may be to generate a feasible schedule that satisfies the given
constraints (such as sequence of tasks or limited resource availability) or
to optimize a given criterion such as the makespan of the schedule.
Artelys-Kalis defines several aggregate modeling objects to simplify the
formulation of standard scheduling problems like tasks,resources and schedule
objects.
|
| KSchedule.ScheduleStatus |
|
| KSession |
Nothing can be done in Artelys Kalis outside a KSession object.
|
| KSettleDisjunction |
KSettleDisjunction branching scheme
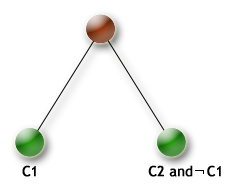
Example : |
| KSmallestDomain |
This class implements a variable selector that selects the first uninstantiated variable with the smallest domain.
Example :
|
| KSmallestDomDegRatio |
This class implements a variable selector that selects first the variable with the smallest ratio domain size / degree in the constraint graph.
Example :
|
| KSmallestEarliestCompletionTime |
Smallest Earliest Completion time task selection heuristic
|
| KSmallestEarliestStartTime |
Smallest Earliest Start time task selection heuristic
|
| KSmallestLatestCompletionTime |
Smallest Latest Completion time task selection heuristic
|
| KSmallestLatestStartTime |
Smallest Latest Start time task selection heuristic
|
| KSmallestMax |
This class implements a variable selector that selects first the variable
with the smallest upperbound.
Example:
|
| KSmallestMin |
This class implements a variable selector that selects the first uninstantiated variable with the smallest value in its domain.
Example :
|
| KSmallestTargetStartTime |
Smallest Target Start time task selection heuristic
|
| KSolution |
This class represents a solution of a KProblem.
Example :
|
| KSolutionArray |
An array of KSolution objects
|
| KSolutionContainer |
This class represent a pool of solution of a KProblem.
Example:
|
| KSolver |
KSolver is the main class for solving problems defined in a KProblem instance.
Once the problem has been fully built, we can begin to look for solutions.
For this, the main class to be used is KSolver, which allows us to :
look for one solution
look for all solutions
look for another solution when we already know some of them
look for the optimal solution according to the problem objective
A KSolver object must be associated to a specific problem.
|
| KSolver.DblAttrib |
Double attributes
|
| KSolver.DblControl |
Double controls
|
| KSolver.IntAttrib |
Integer attributes
|
| KSolver.IntControl |
Integer controls
|
| KSolver.SearchLimitAttrib |
Search limit attributes
|
| KSolver.ToleranceLimitAttrib |
Tolerance limits attributes
|
| KSolverEventListener |
Callbacks for a KSolver events.
|
| KSplitDomain |
SplitDomain Branching scheme
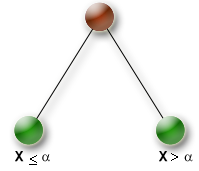
Example : |
| KSplitNumDomain |
SplitDomain Branching scheme

Example : |
| KTask |
Tasks (processing operations, activities) are represented by the class KTask.
|
| KTaskArray |
This class implements an array of KTask
Example :
|
| KTaskInputOrder |
Tasks input order selection heuristic
|
| KTaskRandomOrder |
Tasks random order selection heuristic
|
| KTaskSelector |
Abstract interface class for task selection heuristic
A custom scheduling optimization strategy can be specified by using the
KTaskSerializer branching scheme to select the task to be scheduled and value
choice heuristics for its start and duration variables.
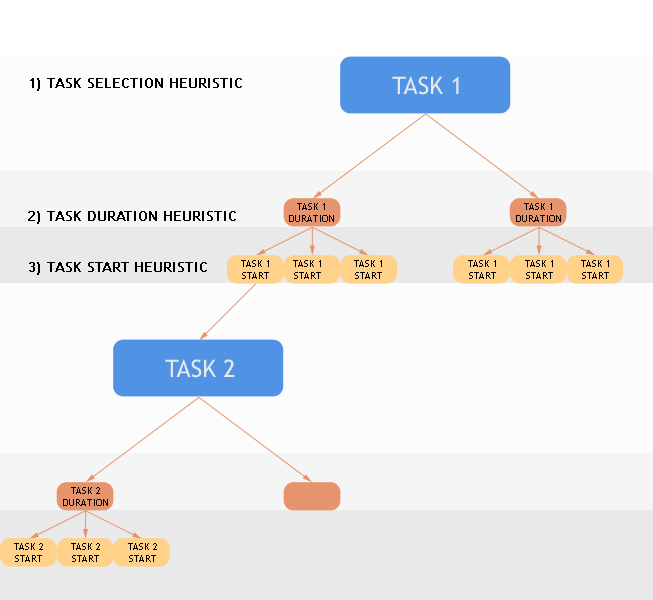
|
| KTaskSerializer |
Task-based branching strategy
A custom scheduling optimization strategy can be specified by using the
KTaskSerializer branching scheme to select the task to be scheduled and value
choice heuristics for its start, duration and assignments variables.

|
| KTaskSerializer.varOrder |
Variable branching orders for each task
|
| KTasksRankConstraint |
Constraint linking tasks and rank variables for unary scheduling.
|
| KTerm |
Superclass of KUnTerm and KBinTerm
|
| KTimeTable |
Timetable object for time-dependant resource usage constraint.
|
| KTopNodeLinearRelaxationSolverConfigurator |
|
| KTupleArray |
This class implements an array of tuples of fixed arity
Example :
|
| KUnaryResource |
Unary Resource
Unary resources can process only one task at a time.
The following schema shows an example with three tasks A,B and C executing
on a disjunctive resource and on a cumulative resource with resource usage 3
for task A, 1 for task B and 1 for task C :

Tasks may require, provide, consume and produce resources :
- A task requires a resource if some amount of the resource capacity must be made available for the execution of the activity. |
| KUnaryResource.PropagationHint |
Propagation Hint Attributes
|
| KUnaryResourceConstraint |
This constraint states that some tasks are not overlapping chronologically.
Resources (machines, raw material etc) can be of two different types :
- Disjunctive when the resource can process only one task at a time (represented by the class KUnaryResource).
- Cumulative when the resource can process several tasks at the same time (represented by the class
KDiscreteResource).
Traditional examples of disjunctive resources are Jobshop problems, cumulative resources are heavily used for the
Resource-Constrained Project Scheduling Problem (RCPSP).
|
| KUnaryResourceConstraint.PropagationLevel |
Differents level of propagation for the constraints
|
| KUnTerm |
This class represent an expression of the form X + cste where X is a variable
and cste , an integer constant
|
| KUserConstraint |
Abstract interface class for definition of user constraints
To create your own constraints in Artelys Kalis, you must create a specific
class that inherits from the KUserConstraint class.
|
| KUserConstraint.askRet |
Return values for `askIfEntailed`
|
| KUserNumConstraint |
The KUserNumConstraint is the generic counterpart to the KUserConstraint for
implementing user constraints when using numeric variables.
|
| KUserNumConstraint.askRet |
askIfEntailed return values
|
| KValueSelector |
Abstract interface class for value selection heuristic
|
| KVariableSelector |
Abstract interface class for variable selection heuristic
|
| KWidestDomain |
This class implements a variable selector that selects the first
uninstantiated variable with the widest domain.
Example :
|
| KXEqualYMinusZ |
This class creates a X == Y - Z constraint
Example :
|
| KXPRSLinearRelaxationSolver |
This linear relaxation solver relies on XPress Optimizer to solve the LP/MIP
problem.
Example:
|







