Constraints examples¶
This chapter contains a collection of examples demonstrating the use of Artelys Kalis for solving different types of (optimization) problems. The first section shows different ways of defining and posting constraints for simple linear constraints. The following sections each introduce a new constraint type.
Constraint all-different : Sudoku¶
Sudoku puzzles, originating from Japan, have recently made their appearance in many western newspapers. The idea of these puzzles is to complete a given, partially filled 9 × 9 board with the numbers 1 to 9 in such a way that no line, column, or 3 × 3 subsquare contains a number more than once. The figures Fig. 8 and Fig. 9 show two instances of such puzzles. Whilst sometimes tricky to solve for a human, these puzzles lend themselves to solving by a constraint programming approach.
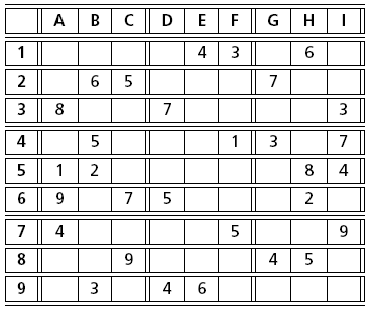
Fig. 8 Sudoku (‘The Times’, 26 January, 2005)¶
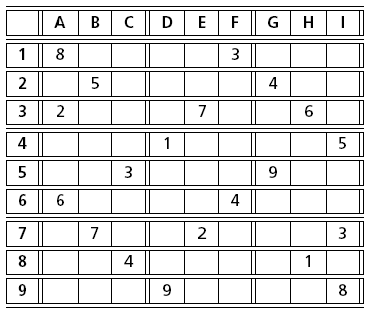
Fig. 9 Sudoku (‘The Guardian’, 29 July, 2005)¶
Model formulation¶
As in the examples, we denote the columns of the board by the set \(XS = \{A, B, ..., I\}\) and the rows by \(YS = \{0, 1, ..., 8\}\). For every \(x\) in \(XS\) and \(y\) in \(YS\) we define a decision variable \(V_{xy}\) taking as its value the number at the position \((x, y)\).
The only constraints in this problem are:
all numbers in a row must be different,
all numbers in a column must be different,
all numbers in a 3 × 3 subsquare must be different.
These constraints can be stated with the KAllDifferent constraint that ensures that all variables in the relation take different values.
In addition, certain variables \(V_{xy}\) are fixed to the given values.
Implementation¶
The implementation for the Sudoku puzzle in figure Fig. 9 looks as follows:
// index variables
int indexX,indexY;
// Creation of the problem in this session
KProblem problem(session,"Sudoku");
// creation of a 9x9 matrix of KintVar
// we use the following bijection: A,B,..,I <-> 0,1,..,8
char name[80];
KIntVar *** vars = new KIntVar **[9];
for (indexX = 0;indexX < 9 ; indexX++)
{
vars[indexX] = new KIntVar * [9];
for (indexY = 0;indexY < 9 ; indexY++)
{
sprintf(name,"v[%i,%i]",indexX,indexY);
vars[indexX][indexY] = new KIntVar(problem,name,1,9);
}
}
// Data from "The Guardian", 29 July, 2005. http://www.guardian.co.uk/sudoku
vars[0][0]->instantiate(8); vars[5][0]->instantiate(3);
vars[1][1]->instantiate(5); vars[6][1]->instantiate(4);
vars[0][2]->instantiate(2); vars[4][2]->instantiate(7); vars[7][2]->instantiate(6);
vars[3][3]->instantiate(1); vars[8][3]->instantiate(5);
vars[2][4]->instantiate(3); vars[6][4]->instantiate(9);
vars[0][5]->instantiate(6); vars[5][5]->instantiate(4);
vars[1][6]->instantiate(7); vars[4][6]->instantiate(2); vars[8][6]->instantiate(3);
vars[2][7]->instantiate(4); vars[7][7]->instantiate(1);
vars[3][8]->instantiate(9); vars[8][8]->instantiate(8);
// All-different values in rows
for (indexX = 0;indexX < 9 ; indexX++)
{
KIntVarArray tmpY;
for (indexY = 0;indexY < 9 ; indexY++)
{
tmpY += *vars[indexX][indexY];
}
problem.post(new KAllDifferent("alldiffVert",tmpY,KAllDifferent::GENERALIZED_ARC_CONSISTENCY));
}
// All-different values in columns
for (indexY = 0;indexY < 9 ; indexY++)
{
KIntVarArray tmpX;
for (indexX = 0;indexX < 9 ; indexX++)
{
tmpX += *vars[indexX][indexY];
}
problem.post(new KAllDifferent("alldiffHoriz",tmpX,KAllDifferent::GENERALIZED_ARC_CONSISTENCY));
}
// All-different values in 3x3 squares
int i,j;
for (j=0;j<3;j++)
{
for (i=0;i<3;i++)
{
KIntVarArray tmpXY;
for (indexY = i*3;indexY < i*3+3 ; indexY++)
{
for (indexX = j*3;indexX < j*3+3 ; indexX++)
{
tmpXY += *vars[indexX][indexY];
}
}
problem.post(new KAllDifferent("alldiff3x3",tmpXY,KAllDifferent::GENERALIZED_ARC_CONSISTENCY));
}
}
// propagating problem
if (problem.propagate())
{
printf("Problem is infeasible\n");
exit(1);
}
// creation of the solver
KSolver solver(problem);
// look for all solutions
int result = solver.findAllSolutions();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();
printf("|-------|-------|-------|\n");
for (indexY = 0;indexY < 9 ; indexY++)
{
printf("| %i %i %i | %i %i %i | %i %i %i |\n",
sol->getValue(*vars[0][indexY]),
sol->getValue(*vars[1][indexY]),
sol->getValue(*vars[2][indexY]),
sol->getValue(*vars[3][indexY]),
sol->getValue(*vars[4][indexY]),
sol->getValue(*vars[5][indexY]),
sol->getValue(*vars[6][indexY]),
sol->getValue(*vars[7][indexY]),
sol->getValue(*vars[8][indexY])
);
if (indexY % 3 == 2)
{
printf("|-------|-------|-------|\n");
}
}
// memory desallocation
for (indexX = 0;indexX < 9 ; indexX++)
{
for (indexY = 0;indexY < 9 ; indexY++)
{
delete vars[indexX][indexY];
}
delete[] vars[indexX];
}
delete[] vars;
import sys, os
from kalis import *
# Creation of the session
session = KSession()
# Creation of the problem in this session
problem = KProblem(session, "Sudoku")
# Creation of a 9x9 matrix of KintVar
vars = [
[
KIntVar(problem, "v[{},{}]".format(i,j), 1, 9)
for j in xrange(9)
]
for i in xrange(9)
]
pb = raw_input("Enter problem to be solved (1 or 2): ")
# Data from "The Guardian", 29 July, 2005. http://www.guardian.co.uk/sudoku
if pb == "1":
vars[0][0].instantiate(8); vars[5][0].instantiate(3)
vars[1][1].instantiate(5); vars[6][1].instantiate(4)
vars[0][2].instantiate(2); vars[4][2].instantiate(7); vars[7][2].instantiate(6)
vars[3][3].instantiate(1); vars[8][3].instantiate(5)
vars[2][4].instantiate(3); vars[6][4].instantiate(9)
vars[0][5].instantiate(6); vars[5][5].instantiate(4)
vars[1][6].instantiate(7); vars[4][6].instantiate(2); vars[8][6].instantiate(3)
vars[2][7].instantiate(4); vars[7][7].instantiate(1)
vars[3][8].instantiate(9); vars[8][8].instantiate(8)
elif pb == "2":
vars[0][3].instantiate(3); vars[0][6].instantiate(5)
vars[1][4].instantiate(4); vars[1][7].instantiate(8)
vars[2][1].instantiate(1); vars[2][3].instantiate(5)
vars[2][4].instantiate(7); vars[2][5].instantiate(9)
vars[2][6].instantiate(4); vars[2][8].instantiate(3)
vars[3][0].instantiate(5); vars[3][2].instantiate(2)
vars[4][2].instantiate(4); vars[4][6].instantiate(1)
vars[5][6].instantiate(9); vars[5][8].instantiate(7)
vars[6][0].instantiate(4); vars[6][2].instantiate(7)
vars[6][3].instantiate(9); vars[6][4].instantiate(1)
vars[6][5].instantiate(5); vars[6][7].instantiate(3)
vars[7][1].instantiate(6); vars[7][4].instantiate(8)
vars[8][2].instantiate(1); vars[8][5].instantiate(3)
else:
print "problem must be 1 or 2, not {}".format(pb)
del session
exit(1)
# All-different values in rows
for i in xrange(9):
tmpI = KIntVarArray()
for j in xrange(9):
tmpI.add(vars[i][j])
problem.post(KAllDifferent("alldiffVert {}".format(i), tmpI, KAllDifferent.GENERALIZED_ARC_CONSISTENCY))
# All-different values in columns
for j in xrange(9):
tmpJ = KIntVarArray()
for i in xrange(9):
tmpJ.add(vars[i][j])
problem.post(KAllDifferent("alldiffHoriz {}".format(j), tmpJ, KAllDifferent.GENERALIZED_ARC_CONSISTENCY))
# All-different values in 3x3 squares
for offsetI in xrange(0,9,3):
for offsetJ in xrange(0,9,3):
tmpIJ = KIntVarArray()
for i in xrange(3):
for j in xrange(3):
tmpIJ.add(vars[i + offsetI][j + offsetJ])
problem.post(KAllDifferent("alldiff3x3 {},{}".format(offsetI, offsetJ), tmpIJ, KAllDifferent.GENERALIZED_ARC_CONSISTENCY))
# Propagate problem
if problem.propagate():
print "Problem is infeasible"
exit(1)
# Solve the problem
solver = KSolver(problem)
solver.findAllSolutions()
# Get solution
sol = problem.getSolution()
# Print solution resume
sol.printResume();
print "|-------|-------|-------|"
for j in xrange(9):
print "| {} {} {} | {} {} {} | {} {} {} |".format(
sol.getValue(vars[0][j]), sol.getValue(vars[1][j]), sol.getValue(vars[2][j]),
sol.getValue(vars[3][j]), sol.getValue(vars[4][j]), sol.getValue(vars[5][j]),
sol.getValue(vars[6][j]), sol.getValue(vars[7][j]), sol.getValue(vars[8][j])
)
if j % 3 == 2:
print "|-------|-------|-------|"
del session
import com.artelys.kalis.*;
import java.io.*;
public class Sudoku {
public static void main(String[] args) {
try {
System.loadLibrary("Kalis"); // uses java option -Djava.library.path=path to find Kalis.dll
System.loadLibrary("KalisJava"); // uses java option -Djava.library.path=path to find KalisJava.dll
KSession session = new KSession();
// Creation of the problem in this session
KProblem problem = new KProblem(session, "Sudoku", 4);
KIntVar[][] vars = new KIntVar[9][9];
int i, j;
for (i = 0; i < 9; i++) {
for (j = 0; j < 9; j++) {
vars[i][j] = new KIntVar(problem, String.format("v[%d,%d]",
i, j), 1, 9);
}
}
System.out.print("Enter problem to be solved (1 or 2): ");
BufferedReader br = new BufferedReader(new InputStreamReader(
System.in));
String pb = br.readLine();
if (pb.equals("1")) {
vars[0][0].instantiate(8);
vars[5][0].instantiate(3);
vars[1][1].instantiate(5);
vars[6][1].instantiate(4);
vars[0][2].instantiate(2);
vars[4][2].instantiate(7);
vars[7][2].instantiate(6);
vars[3][3].instantiate(1);
vars[8][3].instantiate(5);
vars[2][4].instantiate(3);
vars[6][4].instantiate(9);
vars[0][5].instantiate(6);
vars[5][5].instantiate(4);
vars[1][6].instantiate(7);
vars[4][6].instantiate(2);
vars[8][6].instantiate(3);
vars[2][7].instantiate(4);
vars[7][7].instantiate(1);
vars[3][8].instantiate(9);
vars[8][8].instantiate(8);
} else if (pb.equals("2")) {
vars[0][3].instantiate(3);
vars[0][6].instantiate(5);
vars[1][4].instantiate(4);
vars[1][7].instantiate(8);
vars[2][1].instantiate(1);
vars[2][3].instantiate(5);
vars[2][4].instantiate(7);
vars[2][5].instantiate(9);
vars[2][6].instantiate(4);
vars[2][8].instantiate(3);
vars[3][0].instantiate(5);
vars[3][2].instantiate(2);
vars[4][2].instantiate(4);
vars[4][6].instantiate(1);
vars[5][6].instantiate(9);
vars[5][8].instantiate(7);
vars[6][0].instantiate(4);
vars[6][2].instantiate(7);
vars[6][3].instantiate(9);
vars[6][4].instantiate(1);
vars[6][5].instantiate(5);
vars[6][7].instantiate(3);
vars[7][1].instantiate(6);
vars[7][4].instantiate(8);
vars[8][2].instantiate(1);
vars[8][5].instantiate(3);
} else {
throw new RuntimeException(String.format(
"problem must be 1 or 2, not '%s'", pb));
}
// *** Modeling of the problem
i = 0;
for (KIntVar[] row : vars) {
KIntVarArray tmpRow = new KIntVarArray();
for (KIntVar cell : row) {
tmpRow.add(cell);
}
problem.post(new KAllDifferent(
String.format("alldiffHoriz#%d", i++),
tmpRow,
KAllDifferent.PropagationLevel.GENERALIZED_ARC_CONSISTENCY
.swigValue()));
}
for(i = 0; i < 9; i++) {
KIntVarArray tmpCol = new KIntVarArray();
for(j = 0; j < 9; j++) {
tmpCol.add(vars[j][i]);
}
problem.post(new KAllDifferent(
String.format("alldiffVert#%d", i),
tmpCol,
KAllDifferent.PropagationLevel.GENERALIZED_ARC_CONSISTENCY
.swigValue()));
}
int[] offsets = {0,3,6};
for(int offsetI : offsets) {
for(int offsetJ : offsets) {
KIntVarArray tmpSquare = new KIntVarArray();
for(i = offsetI; i < offsetI+3; i++) {
for(j = offsetJ; j < offsetJ+3; j++) {
tmpSquare.add(vars[j][i]);
}
}
problem.post(new KAllDifferent(
String.format("alldiff%dx%d", offsetI, offsetJ),
tmpSquare,
KAllDifferent.PropagationLevel.GENERALIZED_ARC_CONSISTENCY
.swigValue()));
}
}
if (problem.propagate()) {
throw new RuntimeException("Problem is infeasible");
}
KSolver solver = new KSolver(problem);
solver.findAllSolutions();
KSolution sol = problem.getSolution();
sol.printResume();
System.out.println("|-------|-------|-------|");
for(j = 0; j < 9; j++) {
System.out.println(String.format("| %d %d %d | %d %d %d | %d %d %d |",
sol.getValue(vars[0][j]), sol.getValue(vars[1][j]), sol.getValue(vars[2][j]),
sol.getValue(vars[3][j]), sol.getValue(vars[4][j]), sol.getValue(vars[5][j]),
sol.getValue(vars[6][j]), sol.getValue(vars[7][j]), sol.getValue(vars[8][j])));
if (j % 3 == 2)
System.out.println("|-------|-------|-------|");
}
} catch (Exception e) {
e.printStackTrace();
}
}
}
Results¶
The model shown above generates the following output; this puzzle has only one solution, as is usually the case for Sudoku puzzles.
The KAllDifferent constructor takes an optional third argument that allows the user to specify the propagation algorithm to be used for evaluating the constraint. If we change from the default setting (KAllDifferent::FORWARD_CHECKING) to the more aggressive strategy KAllDifferent::GENERALIZED_ARC_CONSISTENCY by adding this choice as the third argument of the constructor of KAllDifferent, we observe that the number of
nodes is reduced to a single node the problem is solved by simply posting the constraints. Whereas the time spent in the search is down to zero, the constraint posting now takes 4-5 times longer (still just a fraction of a second) due to the larger computational overhead of the generalized arc consistency algorithm. Allover, the time for problem definition and solving is reduced to less than a tenth of the previous time. As a general rule, the generalized arc
consistency algorithm achieves stronger pruning (i.e., it removes more values from the domains of the variables). However, due to the increase in computation time its use is not always justified. The reader is therefore encouraged to try both algorithm settings in his models.
Constraint distance: Frequency assignment¶
The area of telecommunications, and in particular mobile telecommunications, gives rise to many different variants of frequency assignment problems. We are given a network of cells (nodes) with requirements of discrete frequency bands. Each cell has a given demand for a number of frequencies (bands). Figure 11.2.1 shows the structure of the network. Nodes linked by an edge are considered as neighbors. They must not be assigned the same frequencies to avoid interference. Furthermore, if a cell uses several frequencies they must all be different by at least 2. The objective is to minimize the total number of frequencies used in the network.
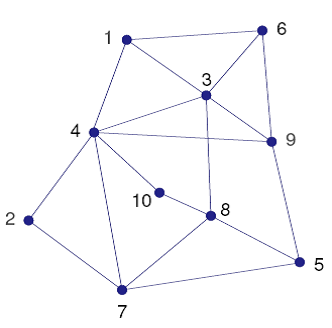
Fig. 11 Telecommunications network¶
The following table lists the number of frequency demands for every cell:
Cell |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Demand |
4 |
5 |
2 |
3 |
2 |
4 |
3 |
4 |
3 |
2 |
Model formulation¶
Let \(NODES\) be the set of all nodes in the network and \(DEM_n\) the demand of frequencies at node \(n \in NODES\). The network is given as a set of edges \(LINKS\). Furthermore, let \(DEMANDS = \{1, 2, . . . ,NUMDEM\}\) be the set of frequencies, numbered consecutively across all nodes where the upper bound \(NUMDEM\) is given by the total number of demands. The auxiliary array \(INDEX_n\) indicates the starting index in \(DEMANDS\) for node \(n\). For representing the frequency assigned to every demand \(d \in DEMANDS\) we introduce the variables \(use\) that take their values from the set \(\{1, 2, . . . ,NUMDEM\}\). The two sets of constraints (different frequencies assigned to neighboring nodes and minimum distance between frequencies within a node) can then be modeled as follows.
The objective function is to minimize to the number of frequencies used. We formulate this by minimizing the largest frequency number that occurs for the \(use\) variables:
Implementation¶
The edges forming the telecommunications network are modeled as a list \(LINK\), where edge \(l\) is given as \((LINK(l,1),LINK(l,2))\). For the implementation of the constraints on the values of frequencies assigned to the same node we have two equivalent choices with Kalis, namely using abs or distance constraints.
const int NODES = 10;
// Range of links between nodes
const int LINKS = 18 ;
// Demand of nodes
int DEM[] = {4, 5, 2, 3, 2, 4, 3, 4, 3, 2};
// Neighboring nodes
int LINK[18][2] = {{1, 3}, {1, 4}, {1, 6},{2, 4}, {2, 7},{3, 4}, {3, 6}, {3, 8}, {3, 9},{4, 7}, {4, 9}, {4,10},{5, 7}, {5, 8}, {5, 9},{6, 9}, {7, 8}, {8,10}};
// Start index in 'use'
int INDEX[10];
// Upper bound on no. of freq.
int NUMDEM;
int n;
NUMDEM = 0;
for (n=0;n<NODES;n++) {
NUMDEM += DEM[n];
}
// Correspondence of nodes and demand indices:
// use[d] d = 0, ..., DEM[1] correspond to the demands of node 0
// d = DEM[0]+1, ..., DEM[0]+DEM(1)) - " - node 2 etc.
INDEX[0] = 0;
for (n=1;n<NODES;n++) {
INDEX[n] = INDEX[n-1] + DEM[n-1];
}
// Creation of the problem in this session
KProblem problem(session,"Frequency assignment");
char name[80];
// Frequency used for a demand
KIntVarArray use;
int d,c;
for (d=0;d<NUMDEM;d++) {
sprintf(name,"use(%i)",d);
use += (* new KIntVar(problem,name,1,NUMDEM) );
}
KIntVar numfreq(problem,"numfreq",0,LINKS);
// All frequencies attached to a node must be different by at least 2
for (n=0;n<NODES;n++) {
for (c=INDEX[n];c<= INDEX[n] + DEM[n] - 1;c++) {
for (d=INDEX[n];d<= INDEX[n] + DEM[n] - 1;d++) {
if (c < d) {
problem.post(KDistanceGreaterThanXyc(use[c],use[d],2));
}
}
}
}
// Neighboring nodes take all-different frequencies
int l;
for (l=0;l<LINKS;l++) {
KIntVarArray diff;
for (d=INDEX[LINK[l][0]-1];d <= INDEX[LINK[l][0]-1] + DEM[LINK[l][0]-1]-1 ;d++) {
diff += use[d];
}
for (d=INDEX[LINK[l][1]-1];d <= INDEX[LINK[l][1]-1] + DEM[LINK[l][1]-1]-1 ;d++) {
diff += use[d];
}
problem.post(KAllDifferent("diff",diff,KAllDifferent::USING_GCC));
}
// Objective function: minimize the number of frequencies used, that is
//minimize the largest value assigned to 'use'
problem.post(KMax("maxuse",numfreq,use,false));
// propagating problem
if (problem.propagate()) {
printf("Problem is infeasible\n");
exit(1);
}
// Search strategy
KBranchingSchemeArray myBa;
myBa += KAssignVar(KSmallestDomain(),KMinToMax(),use);
// Solve the problem
// creation of the solver
KSolver solver(problem,myBa);
solver.setDblControl(KSolver::MaxComputationTime,1.0);
solver.setSolutionFunctionPtr(solution_found,&problem);
// Try to find solution(s) with strategy 1
problem.setSense(KProblem::Minimize);
problem.setObjective(numfreq);
int nsol = -1;
if (solver.optimize()) {
solver.printStats();
KSolution * sol = &problem.getSolution();
nsol = sol->getObjectiveValue();
numfreq.setSup(nsol-1);
}
printf("Number of frequencies: %f\n", problem.getSolution().getObjectiveValue());
printf("Frequency assignment: \n");
for (n=0;n<NODES;n++) {
printf("Node %i: ",n);
for (d=INDEX[n];d<=INDEX[n]+DEM[n]-1;d++) {
printf("%i ",problem.getSolution().getValue(use[d]));
}
printf("\n");
}
// Search strategy
KBranchingSchemeArray myBa2;
myBa2 += KAssignVar(KMaxDegree(),KMinToMax(),use);
// Solve the problem
// creation of the solver
KSolver solver2(problem,myBa2);
solver2.setSolutionFunctionPtr(solution_found,&problem);
// Try to find solution(s) with strategy 2
if (solver2.optimize()) {
solver2.printStats();
KSolution * sol = &problem.getSolution();
}
printf("Number of frequencies: %f\n", problem.getSolution().getObjectiveValue());
printf("Frequency assignment: \n");
for (n=0;n<NODES;n++) {
printf("Node %i: ",n);
for (d=INDEX[n];d<=INDEX[n]+DEM[n]-1;d++) {
printf("%i ",problem.getSolution().getValue(use[d]));
}
printf("\n");
}
import sys
from kalis import *
### Data creation
# Demand of nodes
nodes_demands = [4, 5, 2, 3, 2, 4, 3, 4, 3, 2]
# Neighboring nodes
links = [(1, 3), (1, 4), (1, 6),(2, 4), (2, 7),(3, 4), (3, 6), (3, 8), (3, 9),(4, 7), (4, 9), (4,10),(5, 7), (5, 8), (5, 9),(6, 9), (7, 8), (8,10)]
# Set upper bound and total demand
nb_demands = sum(nodes_demands)
nb_nodes = len(nodes_demands)
nb_links = len(links)
# Correspondance between demands and nodes
demands_index = [0]
for n in range(1, nb_nodes):
demands_index.append(demands_index[n-1] + nodes_demands[n-1])
### Creation of the problem
# Creation of the Kalis session
session = KSession()
# Creation of the optimization problem
problem = KProblem(session, "Frequency assignment")
### Creation of the variables
# One variable for each demand representing the id of the given frequency
use = KIntVarArray()
for d in range(nb_demands):
use += KIntVar(problem, "use(%d)" % n, 1, nb_demands)
# Variable for the objective value:
nb_of_frequencies = KIntVar(problem, 'nb of frequencies', 0, nb_links)
### Creation of the constraints
# All frequencies attached to a node must be different by at least 2
for n in range(nb_nodes):
for d1 in range(demands_index[n], demands_index[n] + nodes_demands[n]):
for d2 in range(d1 + 1, demands_index[n] + nodes_demands[n]):
problem.post(KDistanceGreaterThanXyc(use[d1], use[d2], 2))
# Neighboring nodes take all-different frequencies
for l in links:
diff = KIntVarArray()
# Add all first link node frequencies demands
n1 = l[0] - 1
for d in range(demands_index[n1], demands_index[n1] + nodes_demands[n1]):
diff += use[d]
n2 = l[1] - 1
for d in range(demands_index[n2], demands_index[n2] + nodes_demands[n2]):
diff += use[d]
problem.post(KAllDifferent("diff", diff, KAllDifferent.USING_GCC))
# Objective function: minimize the number of used frequencies, that is minimize the largest
# value assigned in the 'use' array.
problem.post(KMax("maxuse", nb_of_frequencies, use, False))
# Propagate the problem
if problem.propagate():
print("Problem is infeasible")
sys.exit(1)
# Set the search strategy
my_branching_array = KBranchingSchemeArray()
my_branching_array += KAssignVar(KSmallestDomain(), KMinToMax(), use)
### Solve the problem
# Set callback to print solution when a new one is found
class SolutionListener(KSolverEventListener):
def __init__(self, problem):
KSolverEventListener.__init__(self, problem)
def solutionFound(self, solution, thread_id):
solution.printResume()
# creation of the solver
solver = KSolver(problem, my_branching_array)
solver.setDblControl(KSolver.MaxComputationTime, 1.0)
solver.setSolverEventListener(SolutionListener(problem))
# Try to find solution with a first strategy
problem.setSense(KProblem.Minimize)
problem.setObjective(nb_of_frequencies)
nb_of_used_frequencies = -1
if solver.optimize():
solver.printStats()
solution = problem.getSolution()
nb_of_used_frequencies = solution.getObjectiveValue()
nb_of_frequencies.setSup(int(nb_of_used_frequencies) - 1)
print("Number of frequencies: %d" % problem.getSolution().getObjectiveValue())
print("Frequency assignment:")
for n in range(nb_nodes):
print("Node %d: " % (n + 1), end='')
for d in range(demands_index[n], demands_index[n] + nodes_demands[n]):
print("%d " % problem.getSolution().getValue(use[d]), end='')
print("")
# Try to find solution with a second strategy
my_branching_array2 = KBranchingSchemeArray()
my_branching_array2 += KAssignVar(KMaxDegree(), KMinToMax(), use)
solver2 = KSolver(problem, my_branching_array2)
if solver2.optimize():
solver2.printStats()
solution = problem.getSolution()
print("Number of frequencies: %d" % solution.getObjectiveValue())
print("Frequency assignment:")
for n in range(nb_nodes):
print("Node %d: " % (n + 1), end='')
for d in range(demands_index[n], demands_index[n] + nodes_demands[n]):
print("%d " % problem.getSolution().getValue(use[d]), end='')
print("")
int NODES = 10;
// Range of links between nodes
int LINKS = 18 ;
// Demand of nodes
int[] DEM = {4, 5, 2, 3, 2, 4, 3, 4, 3, 2};
// Neighboring nodes
int[][] LINK = {{1, 3}, {1, 4}, {1, 6},{2, 4}, {2, 7},{3, 4}, {3, 6}, {3, 8}, {3, 9},{4, 7}, {4, 9}, {4,10},{5, 7}, {5, 8}, {5, 9},{6, 9}, {7, 8}, {8,10}};
// Start index in 'use'
int[] INDEX = new int[NODES];
// Upper bound on no. of freq.
int NUMDEM;
System.loadLibrary("KalisJava");
try {
NUMDEM = 0;
int indexNode;
for (indexNode=0; indexNode < NODES; indexNode++)
{
NUMDEM += DEM[indexNode];
}
// Correspondence of nodes and demand indices:
// use[d] d = 0, ..., DEM[1] correspond to the demands of node 0
// d = DEM[0]+1, ..., DEM[0]+DEM(1)) - " - node 2 etc.
INDEX[0] = 0;
for (indexNode=1;indexNode<NODES;indexNode++)
{
INDEX[indexNode] = INDEX[indexNode-1] + DEM[indexNode-1];
}
KSession session = new KSession();
// Creation of the problem in this session
KProblem problem = new KProblem(session,"Frequency assignment");
// Frequency used for a demand
KIntVarArray use = new KIntVarArray();
int d,c;
for (d=0;d<NUMDEM;d++) {
use.add(new KIntVar(problem,"use("+d+")",1,NUMDEM) );
}
KIntVar numfreq = new KIntVar(problem,"numfreq",0,LINKS);
// All frequencies attached to a node must be different by at least 2
for (indexNode=0; indexNode<NODES; indexNode++) {
for (c=INDEX[indexNode];c<= INDEX[indexNode] + DEM[indexNode] - 1;c++) {
for (d=INDEX[indexNode];d<= INDEX[indexNode] + DEM[indexNode] - 1;d++) {
if (c < d) {
problem.post(new KDistanceGreaterThanXyc(use.getElt(c),use.getElt(d),2));
}
}
}
}
// Neighboring nodes take all-different frequencies
int l;
for (l=0;l<LINKS;l++) {
KIntVarArray diff = new KIntVarArray();
for (d=INDEX[LINK[l][0]-1];d <= INDEX[LINK[l][0]-1] + DEM[LINK[l][0]-1]-1 ;d++) {
diff.add(use.getElt(d));
}
for (d=INDEX[LINK[l][1]-1];d <= INDEX[LINK[l][1]-1] + DEM[LINK[l][1]-1]-1 ;d++) {
diff.add(use.getElt(d));
}
problem.post(new KAllDifferent("diff",diff,KAllDifferent.PropagationLevel.USING_GCC));
}
// Objective function: minimize the number of frequencies used, that is
//minimize the largest value assigned to 'use'
problem.post(new KMax("maxuse",numfreq,use,false));
// propagating problem
if (problem.propagate()) {
System.out.println("Problem is infeasible");
exit(1);
}
// Search strategy
KBranchingSchemeArray myBa = new KBranchingSchemeArray();
myBa.add(new KAssignVar(new KSmallestDomain(),new KMinToMax(),use));
// Solve the problem
// creation of the solver
KSolver solver = new KSolver(problem,myBa);
solver.setDblControl(KSolver.DblControl.MaxComputationTime,1.0);
// Try to find solution(s) with strategy 1
problem.setSense(KProblem.Sense.Minimize);
problem.setObjective(numfreq);
int nsol = -1;
if (solver.optimize() > 0)
{
solver.printStats();
KSolution sol = problem.getSolution();
nsol = (int) sol.getObjectiveValue();
numfreq.setSup(nsol - 1);
}
System.out.println("Number of frequencies: " + problem.getSolution().getObjectiveValue());
System.out.println("Frequency assignment: ");
for (indexNode=0; indexNode<NODES; indexNode++) {
System.out.println("Node " + indexNode);
for (d=INDEX[indexNode]; d<=INDEX[indexNode]+DEM[indexNode]-1;d++) {
System.out.println(problem.getSolution().getValue(use.getElt(d)));
}
}
// Search strategy
KBranchingSchemeArray myBa2 = new KBranchingSchemeArray();
myBa2.add(new KAssignVar(new KMaxDegree(), new KMinToMax(), use));
// Solve the problem
// creation of the solver
KSolver solver2 = new KSolver(problem,myBa2);
// Try to find solution(s) with strategy 2
if (solver2.optimize() > 0) {
solver2.printStats();
KSolution sol = problem.getSolution();
}
System.out.println("Number of frequencies: " + problem.getSolution().getObjectiveValue());
System.out.println("Frequency assignment: ");
for (indexNode=0; indexNode<NODES; indexNode++)
{
System.out.println("Node " + indexNode);
for (d = INDEX[indexNode]; d <= INDEX[indexNode] + DEM[indexNode] - 1; d++)
{
System.out.println(problem.getSolution().getValue(use.getElt(d)));
}
}
} catch (Exception e)
{
e.printStackTrace();
}
With just the default search strategy this model finds a solution of value 11 but it runs for a long time without being able to prove optimality. When experimenting with different search strategies we have found that the strategy obtained by changing the variable selection criterion to KMaxDegree is able to prove optimality easily once a good solution is known. This problem is therefore solved in two steps: First, we use the default strategy for finding a good solution. This search is stopped after one second by setting a time limit. The search is then restarted with a second strategy and the bound on the objective value from the previous run. Another new feature demonstrated by this implementation is the use of a callback, more precisely the solution callback of Artelys Kalis. The solution callback is defined with a user subroutine that will be called by the solver whenever the search has found a solution. Its typical uses are logging or storing of intermediate solutions or performing some statistics. Our procedure solution_found() simply prints out the solution that has been found.
int solution_found(void *param) {
KProblem * p = (KProblem *) param;
p->getSolution().printResume();
return 0;
}
class SolutionListener(KSolverEventListener):
def __init__(self, problem):
KSolverEventListener.__init__(self, problem)
def solutionFound(self, solution, thread_id):
solution.printResume()
class MySolverEventListener extends KSolverEventListener
{
public void nodeExplored() {
System.out.println("Node explored");
}
public void branchGoDown() {
System.out.println("Branch go down");
}
public void branchGoUp() {
System.out.println("Branch go up");
}
public void branchingScheme() {
}
public boolean stopComputations() {
return false;
}
public void solutionFound() {
System.out.println("A solution has been found!");
}
}
Improving the problem formulation¶
We may observe that in our problem formulation all demand variables within a node and the constraints on these variables are entirely symmetric. In the absence of other constraints, we may reduce these symmetries by imposing an order on the \(use\) variables, \(use_d + 1 \leq use_{d+1}\) for demands \(d\) and \(d+1\) belonging to the same cell. Doing so, the problem is solved to optimality within less than 40 nodes using just the default strategy. We may take this a step further by writing: \(use_d + 2 \leq use_{d+1}\). The addition of these constraints shortens the search by yet a few more nodes. They can even be used simply in replacement of the abs or distance constraints.
Constraint element: Sequencing jobs on a single machine¶
The problem described in this section is taken from Section 7.4 Sequencing jobs on a bottleneck machine of the book Applications of optimization with Xpress-MP. The aim of this problem is to provide a model that may be used with different objective functions for scheduling operations on a single (bottleneck) machine. We shall see here how to minimize the total processing time, the average processing time, and the total tardiness. A set of tasks (or jobs) is to be processed on a single machine. The execution of tasks is nonpreemptive (that is, an operation may not be interrupted before its completion). For every task \(i\) its release date, duration, and due date are given in the following table :
Job |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Release date |
2 |
5 |
4 |
0 |
0 |
8 |
9 |
Duration |
5 |
6 |
8 |
4 |
2 |
4 |
2 |
Due date |
10 |
21 |
15 |
10 |
5 |
15 |
22 |
What is the optimal value for each of the objectives: minimizing the total duration of the schedule (makespan), the mean processing time or the total tardiness (that is, the amount of time by which the completion of jobs exceeds their respective due dates) ?
Model formulation¶
We are going to present a model formulation that is close to the Mathematical Programming formulation in Applications of optimization with Xpress-MP. In model formulation we are going to deal with the different objective functions in sequence, but the body of the models will remain the same. To represent the sequence of jobs we introduce variables \(rank_k\) with \(k \in JOBS = \{1, . . . , NJ\}\) that take as value the number of the job in position (rank) \(k\). Every job \(j\) takes a single position. This constraint can be represented by a KAllDifferent on the \(rank_k\) variables:
The processing time \(dur_k\) for the job in position \(k\) is given by \(DUR_{rank_k}\) (where \(DUR_j\) denotes the duration given in the table in the previous section). Similarly, the release time \(rel_k\) is given by \(REL_{rank_k}\) (where \(REL_j\) denotes the given release date):
If \(start_k\) is the start time of the job at position \(k\), this value must be at least as great as the release date of the job assigned to this position. The completion time \(comp_k\) of this job is the sum of its start time plus its duration:
Another constraint is needed to specify that two jobs cannot be processed simultaneously. The job in position \(k+1\) must start after the job in position \(k\) has finished, hence the following constraints:
Objective 1: The first objective is to minimize the makespan (completion time of the schedule), or, equivalently, to minimize the completion time of the last job (job with rank \(NJ\)). The complete model is then given by the following (where \(MAXTIME\) is a sufficiently large value, such as the sum of all release dates and all durations):
Objective 2: For minimizing the average processing time, we introduce an additional variable \(totComp\) representing the sum of the completion times of all jobs. We add the following constraint to the problem to calculate \(totComp\):
The new objective consists of minimizing the average processing time, or equivalently, minimizing the sum of the job completion times: \(\text{minimize }totComp\)
Objective 3: If we now aim to minimize the total tardiness, we again introduce new variables this time to measure the amount of time that jobs finish after their due date. We write \(late_k\) for the variable that corresponds to the tardiness of the job with rank \(k\). Its value is the difference between the completion time of a job \(j\) and its due date \(DUE_j\). If the job finishes before its due date, the value must be zero. We thus obtain the following constraints:
For the formulation of the new objective function we introduce the variable \(totLate\) representing the total tardiness of all jobs. The objective now is to minimize the value of this variable:
Implementation¶
The implementation below (BottleneckSequencing.cpp) solves the same problem three times, each time with a different objective, and prints the resulting solutions.
// Number of tasks
int NTASKS = 7;
// Release date of tasks
int REL[] = { 2, 5, 4, 0, 0, 8, 9};
// Duration of tasks
int DUR[] = { 5, 6, 8, 4, 2, 4, 2};
// Due date of tasks
int DUE[] = {10, 21, 15, 10, 5, 15, 22};
// Number of job at position k
KIntVarArray rank;
// Start time of job at position k
KIntVarArray start;
// Duration of job at position k
KIntVarArray dur;
// Completion time of job at position k
KIntVarArray comp;
// Release date of job at position k
KIntVarArray rel;
// Creation of the problem in this session
KProblem problem(session,"B-4 Sequencing");
// compute some statistics
int indexTask;
int MAXTIME = 0;
int MINDUR = MAX_INT;
int MAXDUR = 0;
int MINREL = MAX_INT;
int MAXREL = 0;
int MINDUE = MAX_INT;
int MAXDUE = 0;
int SDUR = 0;
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
if (MINDUR > DUR[indexTask]) {
MINDUR = DUR[indexTask];
}
if (MAXDUR < DUR[indexTask]) {
MAXDUR = DUR[indexTask];
}
if (MINREL > REL[indexTask]) {
MINREL = REL[indexTask];
}
if (MAXREL < REL[indexTask]) {
MAXREL = REL[indexTask];
}
if (MINDUE > DUE[indexTask]) {
MINDUE = DUE[indexTask];
}
if (MAXDUE < DUE[indexTask]) {
MAXDUE = DUE[indexTask];
}
SDUR += DUR[indexTask];
}
MAXTIME = MAXREL + SDUR;
char name[80];
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
sprintf(name,"rank(%i)",indexTask);
rank += (* new KIntVar(problem,name,0,NTASKS-1));
}
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
sprintf(name,"start(%i)",indexTask);
start += (* new KIntVar(problem,name,0,MAXTIME));
}
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
sprintf(name,"dur(%i)",indexTask);
dur += (* new KIntVar(problem,name,MINDUR,MAXDUR));
}
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
sprintf(name,"comp(%i)",indexTask);
comp += (* new KIntVar(problem,name,0,MAXTIME));
}
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
sprintf(name,"rel(%i)",indexTask);
rel += (* new KIntVar(problem,name,MINREL,MAXREL));
}
// One position per job
problem.post(KAllDifferent("alldiff(rank)",rank));
// Duration of job at position k
KIntArray idur;
KIntArray irel;
KIntArray idue;
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
idur += DUR[indexTask];
irel += REL[indexTask];
idue += DUE[indexTask];
}
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
KEltTerm kelt(idur,rank[indexTask]);
problem.post(kelt == dur[indexTask]);
// Release date of job at position k
KEltTerm keltrel(irel,rank[indexTask]);
problem.post(keltrel == rel[indexTask]);
}
for (indexTask = 0;indexTask < NTASKS-1; indexTask++) {
// Sequence of jobs
problem.post(start[indexTask+1] >= start[indexTask] + dur[indexTask]);
}
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
// Start times
problem.post(start[indexTask] >= rel[indexTask]);
// Completion times
problem.post(comp[indexTask] == start[indexTask] + dur[indexTask]);
}
// propagating problem
if (problem.propagate()) {
printf("Problem is infeasible\n");
exit(1);
}
// Set the branching strategy
KBranchingSchemeArray myBa;
myBa += KSplitDomain(KSmallestDomain(),KMinToMax());
// creation of the solver
KSolver solver(problem,myBa);
// **********************
// Objective 1: Makespan
// **********************
problem.setObjective(comp[NTASKS-1]);
problem.setSense(KProblem::Minimize);
// look for all solutions
int result = solver.optimize();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();
// solution printing
printf("Completion time: %i\n",problem.getSolution().getValue(comp[NTASKS-1]));
printf("Rel\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",REL[indexTask]);
}
printf("\nDur\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",DUR[indexTask]);
}
printf("\nStart\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",problem.getSolution().getValue(start[indexTask]));
}
printf("\nEnd\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",problem.getSolution().getValue(comp[indexTask]));
}
printf("\nDue\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",DUE[indexTask]);
}
printf("\n");
// ***************************************
// Objective 2: Average completion time:
// ***************************************
KLinTerm totalCompletionTerm;
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
totalCompletionTerm = totalCompletionTerm + comp[indexTask];
}
KIntVar averageCompletion(problem,"average completion",0,1000);
problem.post(averageCompletion == totalCompletionTerm);
problem.setObjective(averageCompletion);
result = solver.optimize();
// solution printing
printf("Completion time: %i\n",problem.getSolution().getValue(comp[NTASKS-1]));
printf("average: %i\n",problem.getSolution().getValue(averageCompletion));
printf("Rel\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",REL[indexTask]);
}
printf("\nDur\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",DUR[indexTask]);
}
printf("\nStart\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",problem.getSolution().getValue(start[indexTask]));
}
printf("\nEnd\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",problem.getSolution().getValue(comp[indexTask]));
}
printf("\nDue\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",DUE[indexTask]);
}
printf("\n");
// *****************************
// Objective 3: total lateness:
// *****************************
// Lateness of job at position k
KIntVarArray late;
// Due date of job at position k
KIntVarArray due;
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
sprintf(name,"due(%i)",indexTask);
due += (* new KIntVar(problem,name,MINDUE,MAXDUE));
sprintf(name,"late(%i)",indexTask);
late += (* new KIntVar(problem,name,0,MAXTIME));
}
// Due date of job at position k
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
KEltTerm keltdue(idue,rank[indexTask]);
problem.post(keltdue == due[indexTask]);
}
KLinTerm totLatTerm;
// building each tasks with fixed time horizon (0..HORIZON)
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
// Late jobs: completion time exceeds the due date
problem.post(late[indexTask] >= (comp[indexTask]) - due[indexTask]);
totLatTerm = totLatTerm + late[indexTask];
}
KIntVar totLate(problem,"total lateness",0,1000);
problem.post(totLate == totLatTerm);
problem.setObjective(totLate);
result = solver.optimize();
// solution printing
printf("Completion time: %i\n",problem.getSolution().getValue(comp[NTASKS-1]));
printf("average: %i\n",problem.getSolution().getValue(averageCompletion));
printf("Tardiness: %i\n",problem.getSolution().getValue(totLate));
printf("Rel\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",REL[indexTask]);
}
printf("\nDur\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",DUR[indexTask]);
}
printf("\nStart\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",problem.getSolution().getValue(start[indexTask]));
}
printf("\nEnd\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",problem.getSolution().getValue(comp[indexTask]));
}
printf("\nDue\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",DUE[indexTask]);
}
printf("\nLate\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",problem.getSolution().getValue(late[indexTask]));
}
printf("\n");
import sys
from kalis import *
### Data creation
nb_tasks = 7
release_dates = [2, 5, 4, 0, 0, 8, 9]
durations = [5, 6, 8, 4, 2, 4, 2]
due_dates = [10, 21, 15, 10, 5, 15, 22]
### Variable creation
# Tasks positions
rank = KIntVarArray()
# Jobs starting dates
jobs_start = KIntVarArray()
# Duration of job for each position
jobs_durations = KIntVarArray()
# Completion time for each position
jobs_completions = KIntVarArray()
# Release date of job for each postion
jobs_release_dates = KIntVarArray()
### Creation of the problem
# Creation of the Kalis session
session = KSession()
# Creation of the optimization problem
problem = KProblem(session, "B-4 Sequencing")
# Compute some statistics
min_duration = min(durations)
max_duration = max(durations)
min_release_date = min(release_dates)
max_realease_date = max(release_dates)
min_due_date = min(due_dates)
max_due_date = max(due_dates)
max_time = max_realease_date + sum(durations)
for task_index in range(nb_tasks):
rank += KIntVar(problem, "rank(%d)" % task_index, 0, nb_tasks - 1)
jobs_start += KIntVar(problem, "start(%d)" % task_index, 0, max_time)
jobs_durations += KIntVar(problem, "dur(%d)" % task_index, min_duration, max_duration)
jobs_completions += KIntVar(problem, "comp(%d)" % task_index, 0, max_time)
jobs_release_dates += KIntVar(problem, "rel(%d)" % task_index, min_release_date, max_realease_date)
### Creation of the constraints
# One position per job
problem.post(KAllDifferent("alldiff(rank)", rank))
# Convert python lists data to KIntArray
K_durations = KIntArray()
K_release_dates = KIntArray()
for task_index in range(nb_tasks):
res = K_durations.add(durations[task_index])
res = K_release_dates.add(release_dates[task_index])
# Corresponding durations and jobs durations variables with a KElement constraint
# i.e. "durations[rank[task_index]] == jobs_durations[task_index]"
for task_index in range(nb_tasks):
duration_kelt = KEltTerm(K_durations, rank[task_index])
problem.post(duration_kelt == jobs_durations[task_index])
release_date_kelt = KEltTerm(K_release_dates, rank[task_index])
problem.post(release_date_kelt == jobs_release_dates[task_index])
# Ordering of starting dates between jobs
for task_index in range(nb_tasks - 1):
problem.post(jobs_start[task_index + 1] >= jobs_start[task_index] + jobs_durations[task_index])
# Ordering start times and release dates
for task_index in range(nb_tasks):
problem.post(jobs_start[task_index] >= jobs_release_dates[task_index])
# Job completion date is equal to its start date plus its duration
for task_index in range(nb_tasks):
problem.post(jobs_completions[task_index] == jobs_start[task_index] + jobs_durations[task_index])
# First propagation of the problem
if problem.propagate():
print("Problem is infeasible")
sys.exit(1)
### Solve the problem
# Set the branching scheme
my_branching_array = KBranchingSchemeArray()
my_branching_array += KSplitDomain(KSmallestDomain(), KMinToMax())
# Creation of the solver
solver = KSolver(problem, my_branching_array)
### Objective 1 : minimize the makespan
problem.setObjective(jobs_completions[nb_tasks - 1])
problem.setSense(KProblem.Minimize)
# Look for all feasible solutions
result = solver.optimize()
# Printing the solution
def printSequencingSolution(solution):
print("Completion time: ", solution.getObjectiveValue())
print("Release dates: ", end='\t')
for task_index in range(nb_tasks):
print(release_dates[task_index], end="\t")
print("\nDurations: ", end='\t')
for task_index in range(nb_tasks):
print(durations[task_index], end="\t")
print("\nStart dates: ", end='\t')
for task_index in range(nb_tasks):
print(solution.getValue(jobs_start[task_index]), end="\t")
print("\nEnd dates: ", end='\t')
for task_index in range(nb_tasks):
print(solution.getValue(jobs_completions[task_index]), end="\t")
print("\nDue dates: ", end='\t')
for task_index in range(nb_tasks):
print(due_dates[task_index], end="\t")
print("")
if result:
solution = problem.getSolution()
solution.printResume()
printSequencingSolution(solution)
### Objective 2: minimize the average completion time
jobs_completions_sum = 0
for task_index in range(nb_tasks):
jobs_completions_sum += jobs_completions[task_index]
# The average completion time is defined as equal to the sum of the completion times since it
# is equivalent for the optimization phase.
average_completion = KIntVar(problem, "average completion", 0, 1000)
problem.post(average_completion == jobs_completions_sum)
problem.setObjective(average_completion)
result = solver.optimize()
if result:
solution = problem.getSolution()
solution.printResume()
printSequencingSolution(solution)
### Objective 3: minimize the average completion time
# Declare lateness of each job as a variable
jobs_lateness = KIntVarArray()
for task_index in range(nb_tasks):
jobs_lateness += KIntVar(problem, "late(%d)" % task_index, 0, max_time)
# Declare due date of each job as a variable
jobs_due_dates = KIntVarArray()
for task_index in range(nb_tasks):
jobs_due_dates += KIntVar(problem, "due(%d)" % task_index, min_due_date, max_due_date)
# Convert python lists to KIntArray
K_due_dates = KIntArray()
for task_index in range(nb_tasks):
res = K_due_dates.add(due_dates[task_index])
# Set due date for each job (i.e. "jobs_due_dates[rank[task_index]] == due_dates[task_index]")
for task_index in range(nb_tasks):
due_date_kelt = KEltTerm(K_due_dates, rank[task_index])
problem.post(due_date_kelt == jobs_due_dates[task_index])
# Adding lateness constraint
lateness_sum = 0
for task_index in range(nb_tasks):
problem.post(jobs_lateness[task_index] >= jobs_completions[task_index] - jobs_due_dates[task_index])
lateness_sum += jobs_lateness[task_index]
total_lateness = KIntVar(problem, "total lateness", 0, nb_tasks * max_time)
problem.post(total_lateness == lateness_sum)
problem.setObjective(total_lateness)
result = solver.optimize()
if result:
solution = problem.getSolution()
print("Completion time: %d" % solution.getValue(jobs_completions[nb_tasks-1]))
print("average: %f" % (solution.getValue(average_completion) / nb_tasks))
print("Tardiness: %d" % solution.getValue(total_lateness))
printSequencingSolution(solution)
// Number of tasks
int NTASKS = 7;
// Release date of tasks
int REL[] = { 2, 5, 4, 0, 0, 8, 9};
// Duration of tasks
int DUR[] = { 5, 6, 8, 4, 2, 4, 2};
// Due date of tasks
int DUE[] = {10, 21, 15, 10, 5, 15, 22};
System.loadLibrary("KalisJava");
try
{
// Number of job at position k
KIntVarArray rank = new KIntVarArray();
// Start time of job at position k
KIntVarArray start = new KIntVarArray();
// Duration of job at position k
KIntVarArray dur = new KIntVarArray();
// Completion time of job at position k
KIntVarArray comp = new KIntVarArray();
// Release date of job at position k
KIntVarArray rel = new KIntVarArray();
KSession session = new KSession();
// Creation of the problem in this session
KProblem problem = new KProblem(session, "B-4 Sequencing");
// compute some statistics
int indexTask;
int MAXTIME = 0;
int MINDUR = Integer.MAX_VALUE;
int MAXDUR = 0;
int MINREL = Integer.MAX_VALUE;
int MAXREL = 0;
int MINDUE = Integer.MAX_VALUE;
int MAXDUE = 0;
int SDUR = 0;
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
if (MINDUR > DUR[indexTask])
{
MINDUR = DUR[indexTask];
}
if (MAXDUR < DUR[indexTask])
{
MAXDUR = DUR[indexTask];
}
if (MINREL > REL[indexTask])
{
MINREL = REL[indexTask];
}
if (MAXREL < REL[indexTask])
{
MAXREL = REL[indexTask];
}
if (MINDUE > DUE[indexTask])
{
MINDUE = DUE[indexTask];
}
if (MAXDUE < DUE[indexTask])
{
MAXDUE = DUE[indexTask];
}
SDUR += DUR[indexTask];
}
MAXTIME = MAXREL + SDUR;
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
rank.add(new KIntVar(problem, "use(" + indexTask + ")", 0, NTASKS - 1));
}
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
start.add(new KIntVar(problem, "start(" + indexTask + ")", 0, MAXTIME));
}
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
dur.add(new KIntVar(problem, "dur(" + indexTask + ")", MINDUR, MAXDUR));
}
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
comp.add(new KIntVar(problem, "comp(" + indexTask + ")", 0, MAXTIME));
}
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
rel.add(new KIntVar(problem, "rel(" + indexTask + ")", MINREL, MAXREL));
}
// One position per job
problem.post(new KAllDifferent("alldiff(rank)", rank));
// Duration of job at position k
KIntArray idur = new KIntArray();
KIntArray irel = new KIntArray();
KIntArray idue = new KIntArray();
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
idur.add(DUR[indexTask]);
irel.add(REL[indexTask]);
idue.add(DUE[indexTask]);
}
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
KEltTerm kelt = new KEltTerm(idur, rank.getElt(indexTask));
problem.post(new KElement(kelt, dur.getElt(indexTask)));
// Release date of job at position k
KEltTerm keltrel = new KEltTerm(irel, rank.getElt(indexTask));
problem.post(new KElement(keltrel, rel.getElt(indexTask)));
}
for (indexTask = 0; indexTask < NTASKS - 1; indexTask++)
{
// Sequence of jobs
// Create the linear combination start.getElt(indexTask+1) - start.getElt(indexTask) - dur.getElt(indexTask))
KLinTerm linearTerm = new KLinTerm();
linearTerm.add(start.getElt(indexTask+1),1);
linearTerm.add(start.getElt(indexTask),-1);
linearTerm.add(dur.getElt(indexTask),-1);
// add the linear combination equality startDates[3] - 1 * startDates[0] - varObj == 0
KNumVarArray intVarArrayToSet = linearTerm.getLvars();
KDoubleArray coeffsToSet = linearTerm.getCoeffs();
problem.post(new KNumLinComb("",coeffsToSet,intVarArrayToSet,0,KNumLinComb.LinCombOperator.GreaterOrEqual));
}
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
// Start times
problem.post(new KGreaterOrEqualXyc(start.getElt(indexTask), rel.getElt(indexTask), 0));
// Completion times
// Create the linear combination comp.getElt(indexTask) - start.getElt(indexTask) - dur.getElt(indexTask)
KLinTerm linearTerm = new KLinTerm();
linearTerm.add(comp.getElt(indexTask),1);
linearTerm.add(start.getElt(indexTask),-1);
linearTerm.add(dur.getElt(indexTask),-1);
// add the linear combination equality startDates[3] - 1 * startDates[0] - varObj == 0
KNumVarArray intVarArrayToSet = linearTerm.getLvars();
KDoubleArray coeffsToSet = linearTerm.getCoeffs();
problem.post(new KNumLinComb("",coeffsToSet,intVarArrayToSet,0,KNumLinComb.LinCombOperator.Equal));
}
// propagating problem
if (problem.propagate())
{
System.out.println("Problem is infeasible");
exit(1);
}
// Set the branching strategy
KBranchingSchemeArray myBa = new KBranchingSchemeArray();
myBa.add(new KSplitDomain(new KSmallestDomain(), new KMinToMax()));
// creation of the solver
KSolver solver = new KSolver(problem, myBa);
// **********************
// Objective 1: Makespan
// **********************
problem.setObjective(comp.getElt(NTASKS - 1));
problem.setSense(KProblem.Sense.Minimize);
// look for all solutions
int result = solver.optimize();
// solution printing
KSolution sol = problem.getSolution();
// print solution resume
sol.printResume();
// solution printing
System.out.println("Completion time: " + problem.getSolution().getValue(comp.getElt(NTASKS - 1)));
System.out.print("Rel\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(REL[indexTask] + "\t");
}
System.out.print("\nDur\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(DUR[indexTask] + "\t");
}
System.out.print("\nStart\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(problem.getSolution().getValue(start.getElt(indexTask)) + "\t");
}
System.out.print("\nEnd\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(problem.getSolution().getValue(comp.getElt(indexTask)) + "\t");
}
System.out.print("\nDue\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(DUE[indexTask] + "\t");
}
System.out.print("\n");
// ***************************************
// Objective 2: Average completion time:
// ***************************************
KLinTerm totalCompletionTerm = new KLinTerm();
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
totalCompletionTerm.add(comp.getElt(indexTask), 1);
}
KIntVar averageCompletion = new KIntVar(problem, "average completion", 0, 1000);
// Create the linear combination averageCompletion - totalCompletionTerm
totalCompletionTerm.add(averageCompletion,-1);
KNumVarArray intVarArrayToSet = totalCompletionTerm.getLvars();
KDoubleArray coeffsToSet = totalCompletionTerm.getCoeffs();
problem.post(new KNumLinComb("",coeffsToSet,intVarArrayToSet,0,KNumLinComb.LinCombOperator.Equal));
problem.setObjective(averageCompletion);
result = solver.optimize();
// solution printing
System.out.println("Completion time: " + problem.getSolution().getValue(comp.getElt(NTASKS - 1)));
System.out.println("average: " + problem.getSolution().getValue(averageCompletion));
System.out.print("\nRel\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(REL[indexTask] + "\t");
}
System.out.print("\nDur\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(DUR[indexTask] + "\t");
}
System.out.print("\nStart\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(problem.getSolution().getValue(start.getElt(indexTask)) + "\t");
}
System.out.print("\nEnd\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(problem.getSolution().getValue(comp.getElt(indexTask)) + "\t");
}
System.out.print("\nDue\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(DUE[indexTask] + "\t");
}
System.out.print("\n");
// *****************************
// Objective 3: total lateness:
// *****************************
// Lateness of job at position k
KIntVarArray late = new KIntVarArray();
// Due date of job at position k
KIntVarArray due = new KIntVarArray();
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
due.add(new KIntVar(problem, "due(" + indexTask + ")", MINDUE, MAXDUE));
late.add(new KIntVar(problem, "late(" + indexTask + ")", 0, MAXTIME));
}
// Due date of job at position k
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
KEltTerm keltdue = new KEltTerm(idue, rank.getElt(indexTask));
problem.post(new KElement(keltdue, due.getElt(indexTask)));
}
KLinTerm totLatTerm = new KLinTerm();
// building each tasks with fixed time horizon (0..HORIZON)
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
// Late jobs: completion time exceeds the due date
// Create the linear combination late.getElt(indexTask) - comp.getElt(indexTask) + due.getElt(indexTask)
KLinTerm linearTerm = new KLinTerm();
linearTerm.add(late.getElt(indexTask),1);
linearTerm.add(comp.getElt(indexTask),-1);
linearTerm.add(due.getElt(indexTask),+1);
// add the linear combination equality startDates[3] - 1 * startDates[0] - varObj == 0
KNumVarArray intVarArrayToSet_linearTerm = linearTerm.getLvars();
KDoubleArray coeffsToSet_linearTerm = linearTerm.getCoeffs();
problem.post(new KNumLinComb("",coeffsToSet_linearTerm,intVarArrayToSet_linearTerm,0,KNumLinComb.LinCombOperator.GreaterOrEqual));
totLatTerm.add(late.getElt(indexTask), 1);
}
KIntVar totLate = new KIntVar(problem, "total lateness", 0, 1000);
totLatTerm.add(totLate,-1);
// add the linear combination equality startDates[3] - 1 * startDates[0] - varObj == 0
KNumVarArray intVarArrayToSet_totLatTerm = totLatTerm.getLvars();
KDoubleArray coeffsToSet_totLatTerm = totLatTerm.getCoeffs();
problem.post(new KNumLinComb("",coeffsToSet_totLatTerm,intVarArrayToSet_totLatTerm,0,KNumLinComb.LinCombOperator.Equal));
problem.setObjective(totLate);
result = solver.optimize();
// solution printing
System.out.println("Completion time: " + problem.getSolution().getValue(comp.getElt(NTASKS - 1)));
System.out.println("average: " + problem.getSolution().getValue(averageCompletion));
System.out.println("Tardiness: " + problem.getSolution().getValue(totLate));
System.out.print("\nRel\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(REL[indexTask] + "\t");
}
System.out.print("\nDur\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(DUR[indexTask] + "\t");
}
System.out.print("\nStart\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(problem.getSolution().getValue(start.getElt(indexTask)) + "\t");
}
System.out.print("\nEnd\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(problem.getSolution().getValue(comp.getElt(indexTask)) + "\t");
}
System.out.print("\nDue\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(DUE[indexTask] + "\t");
}
System.out.print("\nLate\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(problem.getSolution().getValue(late.getElt(indexTask)) + "\t");
}
System.out.print("\n");
}
catch (Exception e)
{
e.printStackTrace();
}
Results¶
The minimum makespan of the schedule is 31, the minimum sum of completion times is 103 (which gives an average of 103 / 7 = 14. 71). A schedule with this objective value is 5 \(\rightarrow\) 4 \(\rightarrow\) 1 \(\rightarrow\) 6 \(\rightarrow\) 2 \(\rightarrow\) 3. If we compare the completion times with the due dates we see that jobs 1, 2, 3, and 6 finish late (with a total tardiness of 21). The minimum tardiness is 18. A schedule with this tardiness is 5 \(\rightarrow\) 1 \(\rightarrow\) 4 \(\rightarrow\) 6 \(\rightarrow\) 2 \(\rightarrow\) 7 \(\rightarrow\) 3 where jobs 4 and 7 finish one time unit late and job 3 is late by 16 time units, and it terminates at time 31 instead of being ready at its due date, time 15. This schedule has an average completion time of 15.71.
Constraint occurrence: Sugar production¶
The problem description in this section is taken from Section 6.4 Cane sugar production of the book Applications of optimization with Xpress-MP. The harvest of cane sugar in Australia is highly mechanized. The sugar cane is immediately transported to a sugarhouse in wagons that run on a network of small rail tracks. The sugar content of a wagonload depends on the field it has been harvested from and on the maturity of the sugar cane. Once harvested, the sugar content decreases rapidly through fermentation and the wagonload will entirely lose its value after a certain time. At this moment, eleven wagons loaded with the same quantity have arrived at the sugarhouse. They have been examined to find out the hourly loss and the remaining life span (in hours) of every wagon, these data are summarized in the following table:
Lot |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Loss (kg/h) |
43 |
26 |
37 |
28 |
13 |
54 |
62 |
49 |
19 |
28 |
30 |
Life span (h) |
8 |
8 |
2 |
8 |
4 |
8 |
8 |
8 |
8 |
8 |
8 |
Every lot may be processed by any of the three, fully equivalent production lines of the sugarhouse. The processing of a lot takes two hours. It must be finished at the latest at the end of the life span of the wagonload. The manager of the sugarhouse wishes to determine a production schedule for the currently available lots that minimizes the total loss of sugar.
Model formulation¶
Let \(WAGONS = {1, ..., NW}\) be the set of wagons, \(NL\) the number of production lines and \(DUR\) the duration of the production process for every lot. The hourly loss for every wagon \(w\) is given by \(LOSS_w\) and its life span by \(LIFE_w\). We observe that, in an optimal solution, the production lines need to work without any break otherwise we could reduce the loss in sugar by advancing the start of the lot that follows the break. This means that the completion time of every lot is of the form \(s \times DUR\), with \(s > 0\) and is an integer. The maximum value of \(s\) is the number of time slots (of length \(DUR\)) that the sugarhouse will work, namely \(NS = \text{ceil}(NW / NL)\), where ceil stands for rounded to the next largest integer. If \(NW / NL\) is an integer, every line will process exactly \(NS\) lots. Otherwise, some lines will process \(NS - 1\) lots, but at least one line processes \(NS\) lots. In all cases, the length of the optimal schedule is \(NS \times DUR\) hours. We call \(SLOTS = \{1 ,... ,NS\}\) the set of time slots. Every lot needs to be assigned to a time slot. We define variables \(process_w\) for the time slot assigned to wagon \(w\) and variables \(loss_w\) for the loss incurred by this wagonload. Every time slot may take up to \(NL\) lots because there are \(NL\) parallel lines; therefore, we limit the number of occurrences of time slot values among the \(process_w\) variables (this constraint relation is often called cardinality constraint) :
The loss of sugar per wagonload \(w\) and time slot \(s\) is \(COST_{w,s} = s \times DUR \times LOSS_w\). Let variables \(loss_w\) denote the loss incurred by wagon load \(w\):
The objective function (total loss of sugar) is then given as the sum of all losses:
Implementation¶
The following model is the implementation of this problem. It uses the function ceil to calculate the maximum number of time slots. The constraints on the processing variables are expressed by occurrence relations and the losses are obtained via element constraints. The branching strategy uses the variable selection criterion KLargestMin, that is, choosing the variable with the largest lower bound.
// Number of wagon loads of sugar
int NW = 11;
// Number of production lines
int NL = 3;
// Time slots for production
int NS = ceil(NW/((float)NL));
// Loss in kg/hour
int LOSS[] = { 43 ,26, 37, 28, 13, 54, 62, 49, 19, 28 ,30};
// Remaining time per lot (in hours)
int LIFE[] = { 8 , 8, 2, 8 , 4 , 8 , 8, 8, 6, 8 , 8};
// Cost per wagon
KIntArray COST;
// Duration of the production
int DUR = 2;
// Loss per wagon
KIntVarArray loss;
// Time slots for wagon loads
KIntVarArray process;
// Objective variable
KIntVar * totalLoss;
// Creation of the problem in this session
KProblem problem(session,"A-4 Cane sugar production 1");
int w;
// Variables creation
char name[80];
for (w=0;w<NW;w++) {
sprintf(name,"process(%i)",w);
process += (* new KIntVar(problem,name,0,NS-1) ) ;
}
for (w=0;w<NW;w++) {
sprintf(name,"loss(%i)",w);
loss += (* new KIntVar(problem,name,0,10000) ) ;
}
int s;
// Wagon loads per time slot
for (s=0; s < NS; s++) {
KOccurTerm oc(s, process);
problem.post(new KOccurrence(oc, NL, false, true));
}
// Limit on raw product life
for (w = 0; w < NW; w++) {
process[w].setSup(floor(LIFE[w]/((float)DUR))-1);
}
// initialization of COST array
for (s = 0; s < NS; s++) {
COST += 0;
}
KLinTerm totLossTerm;
// Objective function: total loss
for (w = 0; w < NW; w++) {
for (s=0;s<NS;s++) {
COST[s] = (s+1)*DUR*LOSS[w];
}
KEltTerm kelt(COST,process[w]);
problem.post(new KElement(kelt, loss[w],"element"));
totLossTerm = totLossTerm + loss[w];
}
totalLoss = new KIntVar(problem,"totalLoss",0,10000);
problem.post(totLossTerm == *totalLoss);
// propagating problem
if (problem.propagate()) {
printf("Problem is infeasible\n");
exit(1);
}
// search strategy customization
KBranchingSchemeArray myBa;
myBa += KAssignVar(KSmallestMax(),KMinToMax(),process);
// Solve the problem
// creation of the solver
KSolver solver(problem,myBa);
// setting objective and sense of optimization
problem.setSense(KProblem::Minimize);
problem.setObjective(*totalLoss);
int result = solver.optimize();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();
// Solution printing
printf("Total loss: %i\n", sol->getValue(*totalLoss));
for (s = 0; s < NS; s++) {
printf("Slot %i: ", s);
for (w=0;w<NW;w++) {
if (sol->getValue(process[w]) == s) {
printf("wagon %i (%i) ",w,(s+1)*DUR*LOSS[w]);
}
}
printf("\n");
}
from kalis import *
import math
### Data
nb_wagons = 11
nb_production_lines = 3
nb_time_slots = math.ceil(nb_wagons / float(nb_production_lines))
# Loss in kg/hour
wagons_loss_rate = [43, 26, 37, 28, 13, 54, 62, 49, 19, 28, 30]
wagons_life_span = [8, 8, 2, 8, 4, 8, 8, 8, 6, 8, 8]
# Duration of the production
production_duration = 2
### Creation of the problem
# Creation of the Kalis session
session = KSession()
# Creation of the optimization problem
problem = KProblem(session, "A-4 Cane sugar production 1")
### Variables creation
# Loss per wagon
wagon_loss = KIntVarArray()
for w in range(nb_wagons):
wagon_loss += KIntVar(problem, "loss(%d)" % w, 0 , 10000)
# Time slots for wagon loads
wagon_process = KIntVarArray()
for w in range(nb_wagons):
wagon_process += KIntVar(problem, "process(%d)" % w, 0, nb_time_slots - 1)
### Set constraints
# Set the cardinality constraint
for s in range(nb_time_slots):
oc = KOccurTerm(s, wagon_process)
problem.post(KOccurrence(oc, nb_production_lines, False, True))
# limit on raw product life:
for w in range(nb_wagons):
wagon_process[w].setSup(math.floor(wagons_life_span[w] / float(production_duration)) - 1)
# Set the each wagon loss according to its processing order
for w in range(nb_wagons):
# Set cost per wagon
cost = KIntArray()
for t in range(nb_time_slots):
res = cost.add( (t + 1) * production_duration * wagons_loss_rate[w] )
# Add KElement constraint
kelt = KEltTerm(cost, wagon_process[w])
problem.post(KElement(kelt, wagon_loss[w], "element(%d)" % w))
# Objective value
wagons_loss_sum = 0
for w in range(nb_wagons):
wagons_loss_sum += wagon_loss[w]
total_loss = KIntVar(problem, "totalLoss", 0, 10000)
problem.post(total_loss == wagons_loss_sum)
# First propagation to check inconsistency
if problem.propagate():
print("Problem is infeasible")
sys.exit(1)
### Solve the problem
# Search strategy customization
my_branching_scheme = KBranchingSchemeArray()
my_branching_scheme += KAssignVar(KSmallestMax(), KMinToMax(), wagon_process)
# Set the solver
solver = KSolver(problem, my_branching_scheme)
# Setting objective and sense of optimization
problem.setSense(KProblem.Minimize)
problem.setObjective(total_loss)
# Run optimization
result = solver.optimize()
if result:
solution = problem.getSolution()
solution.printResume()
print("Total loss:", solution.getValue(total_loss))
for t in range(nb_time_slots):
print("Slot %d:" % t, end='')
for w in range(nb_wagons):
if solution.getValue(wagon_process[w]) == t:
print(" wagon %d (%d)" % (w, (t + 1) * production_duration * wagons_loss_rate[w]), end='')
print("")
// Number of wagon loads of sugar
int NW = 11;
// Number of production lines
int NL = 3;
// Time slots for production
int NS = (int) Math.ceil(NW / (float) NL);
// Loss in kg/hour
int[] LOSS = {43, 26, 37, 28, 13, 54, 62, 49, 19, 28, 30};
// Remaining time per lot (in hours)
int[] LIFE = {8, 8, 2, 8, 4, 8, 8, 8, 6, 8, 8};
// Cost per wagon
KIntArray COST = new KIntArray();
// Duration of the production
int DUR = 2;
// Loss per wagon
KIntVarArray loss = new KIntVarArray();
// Time slots for wagon loads
KIntVarArray process = new KIntVarArray();
// Objective variable
KIntVar totalLoss = new KIntVar();
// Creation of the session
KSession session = new KSession();
// Creation of the problem in this session
KProblem problem = new KProblem(session, "A-4 Cane sugar production 1");
int w;
// Variables creation
for (w = 0; w < NW; w++)
{
process.add(new KIntVar(problem, "process(" + w + ")", 0, NS - 1));
}
for (w = 0; w < NW; w++)
{
loss.add(new KIntVar(problem, "loss(" + w + ")", 0, 10000));
}
int s;
// Wagon loads per time slot
for (s = 0; s < NS; s++)
{
KOccurTerm oc = new KOccurTerm(s, process);
problem.post(new KOccurrence(oc, NL, false, true));
}
// Limit on raw product life
for (w = 0; w < NW; w++)
{
process.getElt(w).setSup(Math.floor(LIFE[w] / DUR) - 1);
}
KLinTerm totLossTerm = new KLinTerm();
// Objective function: total loss
for (w = 0; w < NW; w++)
{
for (s = 0; s < NS; s++)
{
COST.add((s + 1) * DUR * LOSS[w]);
}
KEltTerm kelt = new KEltTerm(COST,process.getElt(w));
problem.post(new KElement(kelt, loss.getElt(w),"element"));
totLossTerm.add(loss.getElt(w),1);
}
totalLoss = new KIntVar(problem,"totalLoss",0,10000);
KNumVarArray intVarArrayToSet = totLossTerm.getLvars();
KDoubleArray coeffsToSet = totLossTerm.getCoeffs();
intVarArrayToSet.add(totalLoss);
coeffsToSet.add(-1);
problem.post(new KNumLinComb("",coeffsToSet,intVarArrayToSet,0,KNumLinComb.LinCombOperator.Equal));
// propagating problem
if (problem.propagate())
{
System.out.println("Problem is infeasible");
exit(1);
}
// search strategy customization
KBranchingSchemeArray myBa = new KBranchingSchemeArray();
myBa.add(new KAssignVar(new KSmallestMax(), new KMinToMax(), process));
// Solve the problem
// creation of the solver
KSolver solver = new KSolver(problem, myBa);
// setting objective and sense of optimization
problem.setSense(KProblem.Sense.Minimize);
problem.setObjective(totalLoss);
int result = solver.optimize();
// solution printing
KSolution sol = problem.getSolution();
// print solution resume
sol.printResume();
// Solution printing
System.out.println("Total loss: " + sol.getValue(totalLoss));
for (s = 0; s < NS; s++)
{
System.out.print("Slot " + s + " :");
for (w = 0; w < NW; w++)
{
if (sol.getValue(process.getElt(w)) == s)
{
System.out.print("wagon " + w + " (" + (s + 1) * DUR * LOSS[w] + ")");
}
}
System.out.println();
}
An alternative formulation of the constraints on the processing variables is to replace the KOccurrence constraints by a single KGlobalCardinalityConstraint, indicating for every time slot the minimum and maximum number (\(MINUSE_s = 0\) and \(MAXUSEs = NL\)) of production lines that may be used.
int * vals = new int[NS];
int * low = new int[NS];
int * upp = new int[NS];
for (s=0;s<NS;s++) {
vals[s] = s;
low[s] = 0;
upp[s] = NL;
}
problem.post(new KGlobalCardinalityConstraint("Wagon_loads_per_time_slot\0", process, vals, low, upp, NS));
delete[] vals;
delete[] low;
delete[] upp;
vals = KIntArray()
low = KIntArray()
upp = KIntArray()
for t in range(nb_time_slots):
res = vals.add(t)
res = low.add(0)
res = upp.add(nb_production_lines)
problem.post(KGlobalCardinalityConstraint("Wagon_loads_per_time_slot", wagon_process, vals, low, upp, nb_time_slots))
KIntArray vals = new KIntArray();
KIntArray low = new KIntArray();
KIntArray upp = new KIntArray();
for (s = 0; s < NS; s++)
{
vals.add(s);
low.add(0);
upp.add(NL);
}
problem.post(new KGlobalCardinalityConstraint("Wagon_loads_per_time_slot", process, vals, low, upp, NS));
Yet another formulation of this problem is possible with Artelys Kalis, namely interpreting it as a cumulative scheduling problem where the wagon loads are represented by tasks of unit duration, scheduled on a discrete resource with a capacity corresponding to the number of production lines.
Results¶
We obtain a total loss of 1620 kg of sugar. The corresponding schedule of lots is shown in the following table (there are several equivalent solutions) :
Slot 1 |
Slot 2 |
Slot 3 |
Slot 4 |
lot 3 (74 kg) |
lot 1 (172 kg) |
lot 4 (168 kg) |
lot 2 (208 kg) |
lot 6 (108 kg) |
lot 5 (52 kg) |
lot 9 (114 kg) |
lot 10 (224 kg) |
lot 7 (124 kg) |
lot 8 (196 kg) |
lot 11 (180 kg) |
Implies constraint : Paint production¶
The problem description in this section is taken from Section 7.5 Paint production of the book Applications of optimization with Xpress-MP. As a part of its weekly production a paint company produces five batches of paints, always the same, for some big clients who have a stable demand. Every paint batch is produced in a single production process, all in the same blender that needs to be cleaned between every two batches. The durations of blending paint batches 1 to 5 are respectively 40, 35, 45, 32, and 50 minutes. The cleaning times depend on the colors and the paint types. For example, a long cleaning period is required if an oil-based paint is produced after a water-based paint, or to produce white paint after a dark color. The times are given in minutes in the following table:
CLEAN(i,j) |
1 |
2 |
3 |
4 |
5 |
1 |
0 |
11 |
7 |
13 |
11 |
2 |
5 |
0 |
13 |
15 |
15 |
3 |
13 |
15 |
0 |
23 |
11 |
4 |
9 |
13 |
5 |
0 |
3 |
5 |
3 |
7 |
7 |
7 |
0 |
Since the company also has other activities, it wishes to deal with this weekly production in the shortest possible time (blending and cleaning). Which is the corresponding order of paint batches? The order will be applied every week, so the cleaning time between the last batch of one week and the first of the following week needs to be counted for the total duration of cleaning.
Formulation of model 1¶
As for the problem in section 11.3 we are going to present two alternative model formulations. The first one is closer to the Mathematical Programming formulation in Applications of optimization with Xpress-MP, the second uses a two-dimensional element constraint. Let \(JOBS = \{1, ..., NJ\}\) be the set of batches to produce, \(DUR_j\) the processing time for batch \(j\), and \(CLEAN_{i,j}\) the cleaning time between the consecutive batches \(i\) and \(j\). We introduce decision variables \(succ_j\) taking their values in \(JOBS\), to indicate the successor of every job, and variables \(clean_j\) for the duration of the cleaning after every job. The cleaning time after every job is obtained by indexing \(CLEAN_{i,j}\) with the value of \(succ_j\). We thus have the following problem formulation:
The objective function sums up the processing and cleaning times of all batches. The last (all-different) constraint guarantees that every batch occurs exactly once in the production sequence.
Unfortunately, this model does not guarantee that the solution forms a single cycle. Solving it indeed results in a total duration of 239 with an invalid solution that contains two sub-cycles 1 \(\rightarrow\) 3 \(\rightarrow\) 2 \(\rightarrow\) 1 and 4 \(\rightarrow\) 5 \(\rightarrow\) 4. A first possibility is to add a disjunction excluding this solution to our model and re-solve it iteratively until we reach a solution without sub-cycles.
However, this procedure is likely to become impractical with larger data sets since it may potentially introduce an extremely large number of disjunctions. We therefore choose a different, a-priori formulation of the sub-cycle elimination constraints with a variable \(y_j\) per batch and \((NJ-1)^2\) implication constraints.
The variables \(y_j\) correspond to the position of job \(j\) in the production cycle. With these constraints, job 1 always takes the first position.
Implementation of model 1¶
The implementation of the model formulated in the previous section is quite straightforward. The sub-cycle elimination constraints are implemented as logic relations with implies (a stronger formulation of these constraints is obtained by replacing the implications by equivalences, using KEquiv).
// Number of paint batches (=jobs)
int NJ = 5;
// Durations of jobs
int DUR[] = {40, 35, 45, 32, 50};
// Cleaning times between jobs
int CLEAN[5][5] = {
{ 0, 11, 7, 13, 11 },
{ 5, 0, 13, 15, 15 },
{ 13, 15, 0, 23, 11 },
{ 9, 13, 5, 0, 3 },
{ 3, 7, 7, 7, 0 } };
// Cleaning times after a batch
KIntArray CB;
// Successor of a batch
KIntVarArray succ;
// Cleaning time after batches
KIntVarArray clean;
// Variables for excluding subtours
KIntVarArray y;
// Objective variable
KIntVar * cycleTime;
// Creation of the problem in this session
KProblem problem(session,"B-5 Paint production");
// variables creation
char name[80];
int j,i;
for (j=0;j<NJ;j++) {
sprintf(name,"succ(%i)",j);
succ += (* new KIntVar( problem,name,0,NJ-1) );
succ[j].remVal(j);
sprintf(name,"y(%i)",j);
y += (* new KIntVar( problem,name,0,NJ-1) );
}
// initialization of CB array
for (j=0;j<NJ;j++) {
CB += 0;
}
// Cleaning time after every batch
for (j=0;j<NJ;j++) {
sprintf(name,"clean(%i)",j);
clean += (* new KIntVar( problem,name,0,1000) );
for (i=0;i<NJ;i++) {
CB[i] = CLEAN[j][i];
}
KEltTerm kelt(CB,succ[j]);
problem.post(new KElement(kelt,clean[j],"element"));
}
// objective variable creation
cycleTime = new KIntVar(problem,"cycleTime",0,1000);
// Objective: minimize the duration of a production cycle
KLinTerm cycleTerm;
for (j=0;j<NJ;j++) {
cycleTerm = cycleTerm + clean[j] + DUR[j];
}
problem.post(cycleTerm == *cycleTime);
// One successor and one predecessor per batch
problem.post(new KAllDifferent("alldiff",succ));
// Exclude subtours
for (i=0;i<NJ;i++) {
for (j=1;j<NJ;j++) {
if (i!=j) {
problem.post(new KGuard( succ[i] == j , y[j] == y[i] + 1 ); }
}
}
// propagating problem
if (problem.propagate()) {
printf("Problem is infeasible\n");
exit(1);
}
// Solve the problem
// creation of the solver
KSolver solver(problem);
// setting objective and sense of optimization
problem.setSense(KProblem::Minimize);
problem.setObjective(*cycleTime);
int result = solver.optimize();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();
// Solution printing
printf("Minimum cycle time: %i\n", sol->getValue(*cycleTime));
printf("Sequence of batches:\nBatch Duration Cleaning\n");
int first=0;
do {
printf("%i\t%i\t%i\n", first, DUR[first],sol->getValue(clean[first]));
first = sol->getValue(succ[first]);
} while (first!=0);
from kalis import *
### Data
# Number of paint batches (=jobs)
nb_jobs = 5
# Durations of jobs
jobs_durations = [40, 35, 45, 32, 50]
# Cleaning times between jobs
jobs_cleaning_times = [[0, 11, 7, 13, 11],
[5, 0, 13, 15, 15],
[13, 15, 0, 23, 11],
[9, 13, 5, 0, 3],
[3, 7, 7, 7, 0]]
max_cleaning_time = max(max(jobs_cleaning_times[j]) for j in range(nb_jobs))
### Creation of the problem
# Creation of the Kalis session
session = KSession()
# Creation of the optimization problem
problem = KProblem(session, "B-5 Paint production")
### Variables creation
# Successor of a batch
batch_successor = KIntVarArray()
for j in range(nb_jobs):
batch_successor += KIntVar(problem, "succ(%d)" % j, 0, nb_jobs - 1)
batch_successor[j].remVal(j)
# Cleaning times after a batch
batch_cleaning_time = KIntVarArray()
for j in range(nb_jobs):
batch_cleaning_time += KIntVar(problem, "clean(%d)" % j, 0, max_cleaning_time)
# Variables for excluding subtours
job_position_in_cycle = KIntVarArray() # i.e. y_j variables
for j in range(nb_jobs):
job_position_in_cycle += KIntVar(problem, "y(%d)" % j, 0, nb_jobs - 1)
### Constraints creation
# Cleaning time after every batch:
# i.e. "batch_cleaning_time[j] == jobs_cleaning_times[batch_succesor[j]]"
for j in range(nb_jobs):
K_cleaning_time = KIntArray() # convert Python list to KIntArray
for i in range(nb_jobs):
res = K_cleaning_time.add(jobs_cleaning_times[j][i])
kelt = KEltTerm(K_cleaning_time, batch_successor[j])
problem.post(kelt == batch_cleaning_time[j])
# One successor and on predecessor per batch
problem.post(KAllDifferent("alldiff", batch_successor))
# Exclude subtours
for i in range(nb_jobs):
for j in range(1, nb_jobs):
if i != j:
problem.post( KGuard(batch_successor[i] == j,
job_position_in_cycle[j] == (job_position_in_cycle[i] + 1)))
# Set objective
cycle_time = KIntVar(problem, "cycle_time", 0, 1000)
batch_cleaning_times_sum = 0
for j in range(nb_jobs):
batch_cleaning_times_sum += batch_cleaning_time[j]
problem.post(cycle_time == (batch_cleaning_times_sum + sum(jobs_durations)))
# First propagation to check inconsistency
if problem.propagate():
print("Problem is infeasible")
sys.exit(1)
### Solve the problem
# Set the solver
solver = KSolver(problem)
# Setting objective and sense of optimization
problem.setSense(KProblem.Minimize)
problem.setObjective(cycle_time)
# Run optimization
result = solver.optimize()
# Solution printing
if result:
solution = problem.getSolution()
solution.printResume()
print("Minimum cycle time: %d" % solution.getValue(cycle_time))
print("Sequence of batches:")
print("Batch Duration Cleaning")
j = solution.getValue(batch_successor[0])
while j != 0:
print("%d\t%d\t%d" % (j, jobs_durations[j],
solution.getValue(batch_cleaning_time[j])))
j = solution.getValue(batch_successor[j])
// Number of paint batches (=jobs)
int NJ = 5;
// Durations of jobs
int[] DUR = {40, 35, 45 ,32 ,50};
// Cleaning times between jobs
int[][] CLEAN = {
{ 0, 11, 7, 13, 11 },
{ 5, 0, 13, 15, 15 },
{ 13, 15, 0, 23, 11 },
{ 9, 13, 5, 0, 3 },
{ 3, 7, 7, 7, 0 } };
// Cleaning times after a batch
KIntArray CB = new KIntArray();
// Successor of a batch
KIntVarArray succ = new KIntVarArray();
// Cleaning time after batches
KIntVarArray clean = new KIntVarArray();
// Variables for excluding subtours
KIntVarArray y = new KIntVarArray();
// Objective variable
KIntVar cycleTime = new KIntVar();
// Creation of the problem in this session
KProblem problem = new KProblem(session,"B-5 Paint production");
// variables creation
int j,i;
for (j=0;j<NJ;j++)
{
succ.add(new KIntVar(problem,"succ(" + j + ")",0,NJ-1));
succ.getElt(j).remVal(j);
y.add(new KIntVar(problem,"y(" + j + ")",0,NJ-1));
}
// Cleaning time after every batch
for (j=0;j<NJ;j++)
{
clean.add(new KIntVar(problem,"clean(" + j + ")",0,1000) );
for (i=0;i<NJ;i++)
{
CB.add(CLEAN[j][i]);
}
KEltTerm kelt = new KEltTerm(CB,succ.getElt(j));
problem.post(new KElement(kelt,clean.getElt(j),"element"));
}
// objective variable creation
cycleTime = new KIntVar(problem,"cycleTime",0,1000);
// Objective: minimize the duration of a production cycle
KLinTerm cycleTerm = new KLinTerm();
int sumOfDUR = 0;
for (j=0;j<NJ;j++)
{
cycleTerm.add(clean.getElt(j),1);
sumOfDUR += DUR[j];
}
KNumVarArray intVarArrayToSet = cycleTerm.getLvars();
KDoubleArray coeffsToSet = cycleTerm.getCoeffs();
intVarArrayToSet.add(cycleTime);
coeffsToSet.add(-1);
problem.post(new KNumLinComb("",coeffsToSet,intVarArrayToSet,-sumOfDUR,KNumLinComb.LinCombOperator.Equal));
// One successor and one predecessor per batch
problem.post(new KAllDifferent("alldiff",succ));
// Exclude subtours
for (i=0;i<NJ;i++)
{
for (j=1;j<NJ;j++)
{
if (i!=j)
{
problem.post(new KGuard( new KEqualXc(succ.getElt(i),j) , new KGreaterOrEqualXyc(y.getElt(j),y.getElt(i), 1)));
}
}
}
// propagating problem
if (problem.propagate())
{
System.out.println("Problem is infeasible");
exit(1);
}
// Solve the problem
// creation of the solver
KSolver solver = new KSolver(problem);
// setting objective and sense of optimization
problem.setSense(KProblem.Sense.Minimize);
problem.setObjective(cycleTime);
int result = solver.optimize();
// solution printing
KSolution sol = problem.getSolution();
// print solution resume
sol.printResume();
// Solution printing
System.out.println("Minimum cycle time: " + sol.getValue(cycleTime));
System.out.println("Sequence of batches:");
System.out.println("Batch Duration Cleaning:");
int first=0;
do {
System.out.print(first + "\t" + DUR[first] + "\t" + sol.getValue(clean.getElt(first)) + "\n");
first = sol.getValue(succ.getElt(first));
} while (first!=0);
Formulation of model 2¶
We may choose to implement the paint production problem using rank variables similarly to the sequencing model in section 11.3. As before, let \(JOBS = \{1, ..., NJ\}\) be the set of batches to produce, \(DUR_j\) the processing time for batch \(j\), and \(CLEAN_{i,j}\) the cleaning time between the consecutive batches \(i\) and \(j\). We introduce decision variables \(rank_k\) taking their values in \(JOBS\), for the number of the job in position \(k\). Variables \(clean_k\) with \(k \in JOBS\) now denote the duration of the \(k^{\text{th}}\) cleaning time. This duration is obtained by indexing \(CLEAN_{i,j}\) with the values of two consecutive \(rank_k\) variables. We thus have the following problem formulation.
As in model 1, the objective function sums up the processing and cleaning times of all batches. Although not strictly necessary from the mathematical point of view, we use different sum indices for durations and cleaning times to show the difference between summing over jobs or job positions. We now have an all-different constraint over the rank variables to guarantee that every batch occurs exactly once in the production sequence.
Implementation of model 2¶
The implementation of the second model uses the 2-dimensional version of the KElement constraint in Artelys Kalis.
// Number of paint batches (=jobs)
int NJ = 5;
// Durations of jobs
int DUR[] = {40, 35, 45 ,32 ,50};
// Cleaning times between jobs
KIntMatrix CLEAN(5,5,0,"CLEAN");
CLEAN[0][0] = 0;CLEAN[1][0] = 11;CLEAN[2][0] = 7;CLEAN[3][0] = 13;CLEAN[4][0] = 11;
CLEAN[0][1] = 5;CLEAN[1][1] = 0;CLEAN[2][1] = 13;CLEAN[3][1] = 15;CLEAN[4][1] = 15;
CLEAN[0][2] = 13;CLEAN[1][2] = 15;CLEAN[2][2] = 0;CLEAN[3][2] = 23;CLEAN[4][2] = 11;
CLEAN[0][3] = 9;CLEAN[1][3] = 13;CLEAN[2][3] = 5;CLEAN[3][3] = 0;CLEAN[4][3] = 3;
CLEAN[0][4] = 3;CLEAN[1][4] = 7;CLEAN[2][4] = 7;CLEAN[3][4] = 7;CLEAN[4][4] = 0;
// Successor of a batch
KIntVarArray rank;
// Cleaning time after batches
KIntVarArray clean;
// Objective variable
KIntVar * cycleTime;
// Creation of the problem in this session
KProblem problem(session,"B-5 Paint production");
// variables creation
char name[80];
int k,j,i;
for (j=0;j<NJ;j++) {
sprintf(name,"rank(%i)",j);
rank += (* new KIntVar( problem,name,0,NJ-1) );
sprintf(name,"clean(%i)",j);
clean += (* new KIntVar( problem,name,0,1000) );
}
// Cleaning time after every batch
for (k=0;k<NJ;k++) {
if (k < NJ-1) {
KEltTerm2D kelt(CLEAN,rank[k],rank[k+1]);
problem.post(new KElement2D(kelt,clean[k],"element"));
} else {
KEltTerm2D kelt(CLEAN,rank[k],rank[0]);
problem.post(new KElement2D(kelt,clean[k],"element"));
}
}
// objective variable creation
cycleTime = new KIntVar(problem,"cycleTime",0,1000);
// Objective: minimize the duration of a production cycle
KLinTerm cycleTerm;
for (j=0;j<NJ;j++) {
cycleTerm = cycleTerm + DUR[j];
}
KLinTerm cleanTerm;
for (k=0;k<NJ;k++) {
cleanTerm = cleanTerm + clean[k];
}
problem.post(cycleTerm + cleanTerm == *cycleTime);
// One position for every job
problem.post(new KAllDifferent("alldiff",rank));
// propagating problem
if (problem.propagate()) {
printf("Problem is infeasible\n");
exit(1);
}
// Solve the problem
// creation of the solver
KSolver solver(problem);
// setting objective and sense of optimization
problem.setSense(KProblem::Minimize);
problem.setObjective(*cycleTime);
int result = solver.optimize();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();
// Solution printing
printf("Minimum cycle time: %i\n", sol->getValue(*cycleTime));
printf("Sequence of batches:\nBatch Duration Cleaning\n");
for (k=0;k<NJ;k++) {
printf("%i\t%i\t%i\n", sol->getValue(rank[k]), DUR[sol->getValue(rank[k])], sol->getValue(clean[k]));
}
### Data
# Number of paint batches (=jobs)
nb_jobs = 5
# Durations of jobs
jobs_durations = [40, 35, 45, 32, 50]
# Cleaning times between jobs
jobs_cleaning_times = [[0, 11, 7, 13, 11],
[5, 0, 13, 15, 15],
[13, 15, 0, 23, 11],
[9, 13, 5, 0, 3],
[3, 7, 7, 7, 0]]
max_cleaning_time = max(max(jobs_cleaning_times[j]) for j in range(nb_jobs))
# Setting data as a KIntMatrix
K_cleaning_times_matrix = KIntMatrix(5, 5, 0, "CLEAN")
for i in range(nb_jobs):
for j in range(nb_jobs):
K_cleaning_times_matrix.setMatrix(i, j, jobs_cleaning_times[i][j])
### Creation of the problem
# Creation of the Kalis session
session = KSession()
# Creation of the problem in this session
problem = KProblem(session, "B-5 Paint production")
### Variable creation
# Successor of a batch
batch_rank = KIntVarArray()
for j in range(nb_jobs):
batch_rank += KIntVar(problem, "rank(%d)" % j, 0, nb_jobs - 1)
# Cleaning time after batches
batch_cleaning_time = KIntVarArray()
for j in range(nb_jobs):
batch_cleaning_time += KIntVar(problem, "clean(%d)" % j, 0, max_cleaning_time)
### Constraints creation
# Set cleaning times after every batch
for k in range(nb_jobs):
if k < nb_jobs - 1:
kelt = KEltTerm2D(K_cleaning_times_matrix, batch_rank[k], batch_rank[k + 1])
problem.post(KElement2D(kelt, batch_cleaning_time[k], "element"))
else:
kelt = KEltTerm2D(K_cleaning_times_matrix, batch_rank[k], batch_rank[0])
problem.post(KElement2D(kelt, batch_cleaning_time[k], "element"))
# One position for every job
problem.post(KAllDifferent("alldiff", batch_rank))
# Set objective
cycle_time = KIntVar(problem, "cycle_time", 0, 1000)
batch_cleaning_times_sum = 0
for j in range(nb_jobs):
batch_cleaning_times_sum += batch_cleaning_time[j]
problem.post(cycle_time == (batch_cleaning_times_sum + sum(jobs_durations)))
# First propagation to check inconsistency
if problem.propagate():
print("Problem is infeasible")
sys.exit(1)
### Solve the problem
# Set the solver
solver = KSolver(problem)
# Setting objective and sense of optimization
problem.setSense(KProblem.Minimize)
problem.setObjective(cycle_time)
# Run optimization
result = solver.optimize()
# Solution printing
if result:
solution = problem.getSolution()
solution.printResume()
print("Minimum cycle time: %d" % solution.getValue(cycle_time))
print("Sequence of batches:")
print("Batch Duration Cleaning")
for k in range(nb_jobs):
job_id = solution.getValue(batch_rank[k])
print("%d\t%d\t%d" % (job_id, jobs_durations[job_id],
solution.getValue(batch_cleaning_time[k])))
// Cleaning times between jobs
KIntMatrix CLEAN = new KIntMatrix(5, 5, 0, "CLEAN");
CLEAN.setMatrix(0, 0, 0);
CLEAN.setMatrix(1,0,11);
CLEAN.setMatrix(2,0,7);
CLEAN.setMatrix(3,0,13);
CLEAN.setMatrix(4,0,11);
CLEAN.setMatrix(0,1,5);
CLEAN.setMatrix(1,1,0);
CLEAN.setMatrix(2,1,13);
CLEAN.setMatrix(3,1,15);
CLEAN.setMatrix(4,1,15);
CLEAN.setMatrix(0,2,13);
CLEAN.setMatrix(1,2,15);
CLEAN.setMatrix(2,2,0);
CLEAN.setMatrix(3,2,23);
CLEAN.setMatrix(4,2,11);
CLEAN.setMatrix(0,3,9);
CLEAN.setMatrix(1,3,13);
CLEAN.setMatrix(2,3,5);
CLEAN.setMatrix(3,3,0);
CLEAN.setMatrix(4,3,3);
CLEAN.setMatrix(0,4,3);
CLEAN.setMatrix(1,4,7);
CLEAN.setMatrix(2,4,7);
CLEAN.setMatrix(3,4,7);
CLEAN.setMatrix(4,4,0);
// Successor of a batch
KIntVarArray rank = new KIntVarArray();
// Cleaning time after batches
KIntVarArray clean = new KIntVarArray();
// Objective variable
KIntVar cycleTime = new KIntVar();
// Creation of the problem in this session
KProblem problem = new KProblem(session, "B-5 Paint production");
// variables creation
int k,j;
for (j=0; j<NJ; j++)
{
rank.add(new KIntVar(problem, "rank(" + j + ")", 0, NJ-1) );
clean.add(new KIntVar(problem, "clean(" + j + ")", 0, 1000) );
}
// Cleaning time after every batch
for (k=0; k<NJ; k++)
{
if (k < NJ-1)
{
KEltTerm2D kelt = new KEltTerm2D(CLEAN, rank.getElt(k), rank.getElt(k+1));
problem.post(new KElement2D(kelt, clean.getElt(k), "element"));
} else {
KEltTerm2D kelt = new KEltTerm2D(CLEAN, rank.getElt(k), rank.getElt(0));
problem.post(new KElement2D(kelt, clean.getElt(k), "element"));
}
}
// objective variable creation
cycleTime = new KIntVar(problem, "cycleTime", 0, 1000);
// Objective: minimize the duration of a production cycle
KLinTerm cleanTerm = new KLinTerm();
int sumOfDUR = 0;
for (j=0; j<NJ; j++)
{
cleanTerm.add(clean.getElt(j),1);
sumOfDUR += DUR[j];
}
KNumVarArray intVarArrayToSet = cleanTerm.getLvars();
KDoubleArray coeffsToSet = cleanTerm.getCoeffs();
intVarArrayToSet.add(cycleTime);
coeffsToSet.add(-1);
problem.post(new KNumLinComb("",coeffsToSet,intVarArrayToSet,sumOfDUR,KNumLinComb.LinCombOperator.Equal));
// One position for every job
problem.post(new KAllDifferent("alldiff",rank));
// propagating problem
if (problem.propagate())
{
System.out.println("Problem is infeasible");
exit(1);
}
// Solve the problem
// creation of the solver
KSolver solver = new KSolver(problem);
// setting objective and sense of optimization
problem.setSense(KProblem.Sense.Minimize);
problem.setObjective(cycleTime);
solver.optimize();
// solution printing
KSolution sol = problem.getSolution();
// print solution resume
sol.printResume();
// Solution printing
System.out.println("Minimum cycle time: " + sol.getValue(cycleTime));
System.out.print("Sequence of batches:\nBatch Duration Cleaning\n");
for (k=0; k<NJ; k++)
{
System.out.print(sol.getValue(rank.getElt(k)) + "\t" + DUR[sol.getValue(rank.getElt(k))] + "\t" + sol.getValue(clean.getElt(k)) + "\n");
}
Results¶
The minimum cycle time for this problem is 243 minutes which is achieved with the following sequence of batches: 1 \(\rightarrow\) 2 \(\rightarrow\) 5 \(\rightarrow\) 3 \(\rightarrow\) 4 \(\rightarrow\) 1. This time includes 202 minutes of (incompressible) processing time and 41 minutes of cleaning.
Equivalence constraint : Location of income tax offices¶
The example description in the following section is taken from Section 15.5 Location of income tax offices of the book Applications of optimization with Xpress-MP. The income tax administration is planning to restructure the network of income tax offices in a region. The number of inhabitants of every city and the distances between each pair of cities are known (see table below). The income tax administration has determined that offices should be established in three cities to provide sufficient coverage. Where should these offices be located to minimize the average distance per inhabitant to the closest income tax office ?
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
0 |
15 |
37 |
55 |
24 |
60 |
18 |
33 |
48 |
40 |
58 |
67 |
2 |
15 |
0 |
22 |
40 |
38 |
52 |
33 |
48 |
42 |
55 |
61 |
61 |
3 |
37 |
22 |
0 |
18 |
16 |
30 |
43 |
28 |
20 |
58 |
39 |
39 |
4 |
55 |
40 |
18 |
0 |
34 |
12 |
61 |
46 |
24 |
62 |
43 |
34 |
5 |
24 |
38 |
16 |
34 |
0 |
36 |
27 |
12 |
24 |
49 |
37 |
43 |
6 |
60 |
52 |
30 |
12 |
36 |
0 |
57 |
42 |
12 |
50 |
31 |
22 |
7 |
18 |
33 |
43 |
61 |
27 |
57 |
0 |
15 |
45 |
22 |
40 |
61 |
8 |
33 |
48 |
28 |
46 |
12 |
42 |
15 |
0 |
30 |
37 |
25 |
46 |
9 |
48 |
42 |
20 |
24 |
24 |
12 |
45 |
30 |
0 |
38 |
19 |
19 |
10 |
40 |
55 |
58 |
62 |
49 |
50 |
22 |
37 |
38 |
0 |
19 |
40 |
11 |
58 |
61 |
39 |
43 |
37 |
31 |
40 |
25 |
19 |
19 |
0 |
21 |
12 |
67 |
61 |
39 |
34 |
43 |
22 |
61 |
46 |
19 |
40 |
21 |
0 |
Pop. (in 1000) |
15 |
10 |
12 |
18 |
5 |
24 |
11 |
16 |
13 |
22 |
19 |
20 |
Model formulation¶
Let \(CITIES\) be the set of cities. For the formulation of the problem, two groups of decision variables are necessary: a variable \(build_c\) that is one if and only if a tax office is established in city \(c\), and a variable \(depend_c\) that takes the number of the office on which city \(c\) depends. For the formulation of the constraints, we further introduce two sets of auxiliary variables: \(depdist_c\), the distance from city \(c\) to the office indicated by \(depend_c\), and \(numdep_c\), the number of cities depending on an office location.
The following relations are required to link the \(build_c\) with the \(depend_c\) variables:
\(numdep_c\) counts the number of occurrences of office location \(c\) among the variables dependc;
\(numdep_c \geq 1\) if and only if the office in \(c\) is built (as a consequence, if the office in \(c\) is not built, then we must have \(numdep_c = 0\));
Since the number of offices built is limited by the given bound \(NUMLOC\), i.e. \(\sum_{c \in CITIES} buil_dc \leq NUMLOC\), it would actually be sufficient to formulate the second relation between the \(build_c\) and \(depend_c\) variables as the implication If \(numdep_c \geq 1\) then the office in \(c\) must be built, and inversely, if the office in \(c\) is not built, then we must have \(numdep_c = 0\).
The objective function to be minimized is the total distance weighted by the number of inhabitants of the cities. We need to divide the resulting value by the total population of the region to obtain the average distance per inhabitant to the closest income tax office. The distance \(depdist_c\) from city \(c\) to the closest tax office location is obtained by a discrete function, namely the row \(c\) of the distance matrix \(DIST_{c,d}\) indexed by the value of \(depend_c\):
Implementation¶
To solve this problem, we define a branching strategy with two parts, one for the \(build_c\) variables and a second strategy for the \(depdist_c\) variables. The latter are enumerated using the KSplitDomain branching scheme that divides the domain of the branching variable into several disjoint subsets (instead of assigning a value to the variable). We now pass an array of type KBranchingSchemeArray as the argument to the constructor of KSolver. The different strategies will be applied in their order in this array. Since our enumeration strategy does not explicitly include all decision variables of the problem, Artelys Kalis will enumerate these using the default strategy if any unassigned variables remain after the application of our search strategy.
// Number of cities
int NC = 12;
// Distance matrix
int DIST[12][12];
// Population of cities
int POP[12] = {15, 10, 12 ,18 ,5 ,24, 11, 16, 13, 22, 19 ,20};
// Desired number of tax offices
int NUMLOC = 3;
// 1 if office in city, 0 otherwise
KIntVarArray build;
// Office on which city depends
KIntVarArray depend;
// Distance to tax office
KIntVarArray depdist;
// Number of depending cities per off.
KIntVarArray numdep;
// Objective function variable
KIntVar * totDist;
// Creation of the problem in this session
KProblem problem(session,"J-5 Tax office location");
// index variables
int b,c,d;
// Calculate the distance matrix
// Initialize all distance labels with a sufficiently large value
for (c=0;c<NC;c++) {
for (d=0;d<NC;d++) {
DIST[c][d] = MAX_INT;
}
}
// Set values on the diagonal to 0
for (c=0;c<NC;c++) {
DIST[c][c] = 0;
}
// Length of existing road connections
DIST[0][1] = 15;DIST[0][4] = 24;DIST[0][6] = 18;DIST[1][2] = 22;
DIST[2][3] = 18;DIST[2][4] = 16;DIST[2][8] = 20;DIST[3][5] = 12;
DIST[4][7] = 12;DIST[4][8] = 24;DIST[5][8] = 12;DIST[5][11] = 22;
DIST[6][7] = 15;DIST[6][9] = 22;DIST[7][8] = 30;DIST[7][10] = 25;
DIST[8][10] = 19;DIST[8][11] = 19;DIST[9][10] = 19;DIST[10][11] = 21;
// distances are symetric
for (b=0;b<NC;b++) {
for (c=0;c<NC;c++) {
if (DIST[b][c] != MAX_INT) {
DIST[c][b] = DIST[b][c];
}
}
}
// Update shortest distance for every node triple
for (b=0;b<NC;b++) {
for (c=0;c<NC;c++) {
for (d=0;d<NC;d++) {
if (c<d) {
if (DIST[c][d] > DIST[c][b]+DIST[b][d]) {
DIST[c][d] = DIST[c][b]+DIST[b][d];
DIST[d][c] = DIST[c][b]+DIST[b][d];
}
}
}
}
}
// total popuplation
int sumPop=0;
char name[80];
// building variables
for (c=0;c<NC;c++) {
sprintf(name,"build(%i)",c);
build += (* new KIntVar(problem,name,0,1) );
sprintf(name,"depend(%i)",c);
depend += (* new KIntVar(problem,name,0,NC-1) );
int dmin=DIST[c][0];
int dmax=DIST[c][0];
int d;
for (d=1;d<NC;d++) {
if (DIST[d][c] < dmin) {
dmin = DIST[c][d];
}
if (DIST[c][d] > dmax) {
dmax = DIST[c][d];
}
}
sprintf(name,"depdist(%i)",c);
depdist += (* new KIntVar(problem,name,dmin,dmax) );
sprintf(name,"numdep(%i)",c);
numdep += (* new KIntVar(problem,name,0,NC) );
// compute total popuplation for solution printing routines
sumPop += POP[c];
}
// Distance from cities to tax offices
for (c=0;c<NC;c++) {
// Auxiliary array used in constr. def.
KIntArray D;
for (d=0;d<NC;d++) {
D += DIST[d][c];
}
KEltTerm kelt(D,depend[c]);
problem.post(kelt == depdist[c]);
}
// Number of cities depending on every office
for (c=0;c<NC;c++) {
KOccurTerm koc(c,depend);
problem.post(koc == numdep[c]);
}
// Relations between dependencies and offices built
for (c=0;c<NC;c++) {
problem.post(KEquiv(build[c] == 1, numdep[c] >= 1));
}
// Limit total number of offices
KLinTerm sbuild;
for (c=0;c<NC;c++) {
sbuild = sbuild + build[c];
}
problem.post(sbuild <= NUMLOC);
// Objective: weighted total distance
totDist = new KIntVar(problem,"totdDist",0,10000);
KLinTerm popDistTerm;
for (c=0;c<NC;c++) {
popDistTerm = popDistTerm + POP[c] * depdist[c];
}
problem.post(popDistTerm == *totDist);
// propagating problem
if (problem.propagate()) {
printf("Problem is infeasible\n");
exit(1);
}
problem.setObjective(*totDist);
problem.setSense(KProblem::Minimize);
// Search strategy
KBranchingSchemeArray myBa;
myBa += KAssignAndForbid(KMaxDegree(),KMaxToMin(),build);
myBa += KSplitDomain(KSmallestDomain(),KMinToMax(),depdist,true,5);
// creation of the solver
KSolver solver(problem,myBa);
// Solve the problem
if (solver.optimize()) {
KSolution * sol = &problem.getSolution();
// do something with optimal solution
}
int totalDist = problem.getSolution().getValue(*totDist);
// Solution printing
printf("Total weighted distance: %d (average per inhabitant: %f\n", totalDist,totalDist / (float)sumPop);
for (c=0;c<NC;c++) {
if (problem.getSolution().getValue(build[c]) > 0) {
printf("Office in %i: ",c);
for (d=0;d<NC;d++) {
if (problem.getSolution().getValue(depend[d]) == c) {
printf(" %i",d);
}
}
printf("\n");
}
}
from kalis import *
### Data
# Number of cities
nb_cities = 12
# Distance matrix
distances = [[float('inf') if c != b else 0 for c in range(nb_cities)] for b in range(nb_cities)]
# Existing roads:
distances[0][1] = 15;distances[0][4] = 24;distances[0][6] = 18;distances[1][2] = 22
distances[2][3] = 18;distances[2][4] = 16;distances[2][8] = 20;distances[3][5] = 12
distances[4][7] = 12;distances[4][8] = 24;distances[5][8] = 12;distances[5][11] = 22
distances[6][7] = 15;distances[6][9] = 22;distances[7][8] = 30;distances[7][10] = 25
distances[8][10] = 19;distances[8][11] = 19;distances[9][10] = 19;distances[10][11] = 21
# Distances are symmetric
for i in range(nb_cities):
for j in range(nb_cities):
if distances[i][j] != float('inf'):
distances[j][i] = distances[i][j]
# Update shortest distance for every node triple
for b in range(nb_cities):
for c in range(nb_cities):
for d in range(c + 1, nb_cities):
if distances[c][d] > distances[c][b] + distances[b][d]:
distances[c][d] = distances[c][b] + distances[b][d]
distances[d][c] = distances[c][b] + distances[b][d]
# Population of cities
populations = [15, 10, 12, 18, 5, 24, 11, 16, 13, 22, 19, 20]
total_population = sum(populations)
# Desired number of tax offices
nb_offices = 3
### Variables creation
# Creation of the Kalis session and of the optimization problem
session = KSession()
problem = KProblem(session, "J-5 Tax office location")
# Building variables: 1 if office in city, 0 otherwise
build = KIntVarArray()
for c in range(nb_cities):
build += KIntVar(problem, "build(%d)" % c, 0, 1)
# Office on which city depends
depend = KIntVarArray()
for c in range(nb_cities):
depend += KIntVar(problem, "depend(%d)" % c, 0, nb_cities - 1)
# Distance to tax office
dep_dist = KIntVarArray()
for c in range(nb_cities):
min_dist = min(distances[c])
max_dist = max(distances[c])
dep_dist += KIntVar(problem, "depdist(%d)" % c, min_dist, max_dist)
# Number of depending cities per off
num_dep = KIntVarArray()
for c in range(nb_cities):
num_dep += KIntVar(problem, "numdep(%d)" % c, 0, nb_cities)
### Constraints creation
# Set distances variables to their corresponding data
for c in range(nb_cities):
# auxiliary array used to set up the constraint
K_dist = KIntArray()
for d in range(nb_cities):
res = K_dist.add(distances[c][d])
# set KElement constraint: "dep_dist[c] == distances[depend[c]]"
kelt = KEltTerm(K_dist, depend[c])
problem.post(kelt == dep_dist[c])
# Set the number of cities depending for each office
for c in range(nb_cities):
koc = KOccurTerm(c, depend)
problem.post(koc == num_dep[c])
# Relations between dependencies and offices built
for c in range(nb_cities):
problem.post(KEquiv(build[c] == 1, num_dep[c] >= 1))
# Limit total number of offices
build_sum = 0
for c in range(nb_cities):
build_sum += build[c]
problem.post(build_sum <= nb_offices)
# Set objective
total_distance = KIntVar(problem, "totDist", 0, 10000)
populations_distance_product = 0
for c in range(nb_cities):
populations_distance_product += populations[c] * dep_dist[c]
problem.post(populations_distance_product == total_distance)
### Solve the problem
# First propagation to check inconsistency
if problem.propagate():
print("Problem is infeasible")
sys.exit(1)
# Setting objective and sense of optimization
problem.setSense(KProblem.Minimize)
problem.setObjective(total_distance)
# Set the branching strategy
myBranchingArray = KBranchingSchemeArray()
# KAssignAndForbid for the "build" variables
myBranchingArray += KAssignAndForbid(KMaxDegree(), KMaxToMin(), build)
# KSplit domain for the "dep_dist" variables ('True' stand for exploring the lower part first,
# '5' stand for the minimum domain size where the domain is not split anymore)
myBranchingArray += KSplitDomain(KSmallestDomain(), KMinToMax(), dep_dist, True, 5)
# Set the solver
solver = KSolver(problem, myBranchingArray)
# Run optimization
result = solver.optimize()
# Solution printing
if result:
solution = problem.getSolution()
solution.printResume()
total_distance_found = solution.getValue(total_distance)
print("Total weighted distance: %f (average per inhabitant: %f)" % (total_distance_found,
total_distance_found / float(total_population)))
for c in range(nb_cities):
if solution.getValue(build[c]) > 0:
print("Office in %d: " % c)
for d in range(nb_cities):
if solution.getValue(depend[d]) == c:
print(d, end=" ")
print("")
// *** Creation of the session
KSession session = new KSession();
// Number of cities
int NC = 12;
// Distance matrix
int DIST[][];
// Population of cities
int POP[] = {15, 10, 12 ,18 ,5 ,24, 11, 16, 13, 22, 19 ,20};
// Desired number of tax offices
int NUMLOC = 3;
// 1 if office in city, 0 otherwise
KIntVarArray build = new KIntVarArray();
// Office on which city depends
KIntVarArray depend = new KIntVarArray();
// Distance to tax office
KIntVarArray depdist = new KIntVarArray();
// Number of depending cities per off.
KIntVarArray numdep = new KIntVarArray();
// Objective function variable
KIntVar totDist = new KIntVar();
// Creation of the problem in this session
KProblem problem = new KProblem(session,"J-5 Tax office location");
// index variables
int b,c,d;
// Calculate the distance matrix
// Initialize all distance labels with a sufficiently large value
DIST = new int[NC][NC];
for (c=0;c<NC;c++)
{
for (d=0;d<NC;d++)
{
DIST[c][d] = 10000000;
}
}
// Set values on the diagonal to 0
for (c=0;c<NC;c++)
{
DIST[c][c] = 0;
}
// Length of existing road connections
DIST[0][1] = 15;
DIST[0][4] = 24;
DIST[0][6] = 18;
DIST[1][2] = 22;
DIST[2][3] = 18;
DIST[2][4] = 16;
DIST[2][8] = 20;
DIST[3][5] = 12;
DIST[4][7] = 12;
DIST[4][8] = 24;
DIST[5][8] = 12;
DIST[5][11] = 22;
DIST[6][7] = 15;
DIST[6][9] = 22;
DIST[7][8] = 30;
DIST[7][10] = 25;
DIST[8][10] = 19;
DIST[8][11] = 19;
DIST[9][10] = 19;
DIST[10][11] = 21;
// distances are symetric
for (b=0;b<NC;b++)
{
for (c=0;c<NC;c++)
{
if (DIST[b][c] != Integer.MAX_VALUE)
{
DIST[c][b] = DIST[b][c];
}
}
}
// Update shortest distance for every node triple
for (b=0;b<NC;b++)
{
for (c=0;c<NC;c++)
{
for (d=0;d<NC;d++)
{
if (c<d)
{
if (DIST[c][d] > DIST[c][b]+DIST[b][d])
{
DIST[c][d] = DIST[c][b]+DIST[b][d];
DIST[d][c] = DIST[c][b]+DIST[b][d];
}
}
}
}
}
// total popuplation
int sumPop=0;
// building variables
for (c=0;c<NC;c++)
{
build.add( new KIntVar(problem,"build("+c+")",0,1) );
depend.add( new KIntVar(problem,"depend("+c+")",0,NC-1) );
int dmin=DIST[c][0];
int dmax=DIST[c][0];
for (d=1;d<NC;d++)
{
if (DIST[d][c] < dmin)
{
dmin = DIST[c][d];
}
if (DIST[c][d] > dmax)
{
dmax = DIST[c][d];
}
//System.out.println("dmin="+dmin);
//System.out.println("dmax="+dmax);
}
depdist.add(new KIntVar(problem,"depdist("+c+")",dmin,dmax) );
numdep.add(new KIntVar(problem,"numdep("+c+")",0,NC) );
// compute total popuplation for solution printing routines
sumPop += POP[c];
}
// Distance from cities to tax offices
for (c=0;c<NC;c++)
{
// Auxiliary array used in constr. def.
KIntArray D = new KIntArray();
for (d=0;d<NC;d++)
{
D.add(DIST[d][c]);
}
KEltTerm kelt = new KEltTerm(D,depend.getElt(c));
//problem.post(kelt == depdist.getElt(c));
problem.post(new KElement(kelt,depdist.getElt(c)));
}
// Number of cities depending on every office
for (c=0;c<NC;c++)
{
KOccurTerm koc = new KOccurTerm(c,depend);
//problem.post(koc == numdep.getElt(c));
problem.post(new KOccurrence(koc,numdep.getElt(c),true,true));
}
// Relations between dependencies and offices built
for (c=0;c<NC;c++)
{
problem.post(new KEquiv(new KEqualXc(build.getElt(c),1), new KGreaterOrEqualXc(numdep.getElt(c),1)));
}
// Limit total number of offices
KLinTerm sbuild = new KLinTerm();
for (c=0;c<NC;c++)
{
sbuild.add(build.getElt(c),1);
}
problem.post(new KNumLinComb("",sbuild.getCoeffs(),sbuild.getLvars(),-NUMLOC,KNumLinComb.LinCombOperator.LessOrEqual));
// Objective: weighted total distance
totDist = new KIntVar(problem,"totdDist",0,10000);
KLinTerm popDistTerm = new KLinTerm();
for (c=0;c<NC;c++)
{
popDistTerm.add( depdist.getElt(c),POP[c]);
}
popDistTerm.add(totDist,-1);
problem.post(new KNumLinComb("",popDistTerm.getCoeffs(),popDistTerm.getLvars(),0,KLinComb.LinCombOperator.Equal));
problem.print();
// propagating problem
if (problem.propagate())
{
System.out.println("Problem is infeasible\n");
System.exit(1);
}
problem.setObjective(totDist);
problem.setSense(KProblem.Sense.Minimize);
// Search strategy
KBranchingSchemeArray myBa = new KBranchingSchemeArray();
myBa.add(new KAssignAndForbid(new KMaxDegree(),new KMaxToMin(),build));
myBa.add(new KSplitDomain(new KSmallestDomain(),new KMinToMax(),depdist,true,5));
// creation of the solver
KSolver solver = new KSolver(problem,myBa);
solver.setSolverEventListener(new MySolverEventListener());
// Solve the problem
if (solver.optimize() != 0) {
KSolution sol = problem.getSolution();
sol.print();
// do something with optimal solution
int totalDist = problem.getSolution().getValue(totDist);
// Solution printing
System.out.println("Total weighted distance: "+totalDist+" (average per inhabitant: "+(totalDist / (float)sumPop));
for (c=0;c<NC;c++) {
if (problem.getSolution().getValue(build.getElt(c)) > 0) {
System.out.print("Office in "+c+" :");
for (d=0;d<NC;d++) {
if (problem.getSolution().getValue(depend.getElt(d)) == c) {
System.out.print(" "+d);
}
}
System.out.println();
}
}
}
Results¶
The optimal solution to this problem has a total weighted distance of 2438. Since the region has a total of 185,000 inhabitants, the average distance per inhabitant is 2438/185 \(\approx\) 13.178 km. The three offices are established at nodes 1, 6, and 11. The first serves cities 1, 2, 5, 7, the office in node 6 cities 3, 4, 6, 9, and the office in node 11 cities 8, 10, 11, 12.
Cycle constraint : Paint production¶
In this section we work once more with the paint production problem. The objective of this problem is to determine a production cycle of minimal length for a given set of jobs with sequence-dependent cleaning times between every pair of jobs.
Model formulation¶
The problem formulation in section 11.5 uses KAllDifferent constraints to ensure that every job occurs once only, calculates the duration of cleaning times with KElement constraints, and introduces auxiliary variables and constraints to prevent subcycles in the production sequence. All these constraints can be expressed by a single constraint relation, the KCycle constraint. Let \(JOBS = \{1, ..., NJ\}\) be the set of batches to produce, \(DUR_j\) the processing time for batch \(j\), and \(CLEAN_{i,j}\) the cleaning time between the consecutive batches \(i\) and \(j\). As before we define decision variables \(succ_j\) taking their values in \(JOBS\), to indicate the successor of every job. The complete model formulation is the following,
where cycle stands for the relation sequence into a single cycle without subcycles or repetitions. The variable cleantime equals the total duration of the cycle.
Implementation¶
The model using the KCycle constraint looks as follows.
// Number of paint batches (=jobs)
int NJ = 5;
// Durations of jobs
int DUR[] = {40, 35, 45 ,32 ,50};
// Cleaning times between jobs
KIntMatrix CLEAN(5,5,0,"CLEAN");
CLEAN[0][0] = 0;CLEAN[1][0] = 11;CLEAN[2][0] = 7;CLEAN[3][0] = 13;CLEAN[4][0] = 11;
CLEAN[0][1] = 5;CLEAN[1][1] = 0;CLEAN[2][1] = 13;CLEAN[3][1] = 15;CLEAN[4][1] = 15;
CLEAN[0][2] = 13;CLEAN[1][2] = 15;CLEAN[2][2] = 0;CLEAN[3][2] = 23;CLEAN[4][2] = 11;
CLEAN[0][3] = 9;CLEAN[1][3] = 13;CLEAN[2][3] = 5;CLEAN[3][3] = 0;CLEAN[4][3] = 3;
CLEAN[0][4] = 3;CLEAN[1][4] = 7;CLEAN[2][4] = 7;CLEAN[3][4] = 7;CLEAN[4][4] = 0;
// Cleaning times after a batch
KIntArray CB;
// Successor of a batch
KIntVarArray succ;
// Objective variable
KIntVar * cycleTime;
// Objective variable
KIntVar * cleanTime;
// Creation of the problem in this session
KProblem problem(session,"B-5 Paint production");
// variables creation
char name[80];
int j,i;
for (j=0;j<NJ;j++) {
sprintf(name,"succ(%i)",j);
succ += (* new KIntVar( problem,name,0,NJ-1) );
succ[j].remVal(j);
}
cleanTime = new KIntVar(problem,"cleanTime",0,1000);
// Assign values to 'succ' variables as to obtain a single cycle
// 'cleanTime' is the sum of the cleaning times
problem.post(new KCycle(&succ, NULL,cleanTime, &CLEAN) );
// objective variable creation
cycleTime = new KIntVar(problem,"cycleTime",0,1000);
// Objective: minimize the duration of a production cycle
KLinTerm cycleTerm;
for (j=0;j<NJ;j++) {
cycleTerm = cycleTerm + DUR[j];
}
problem.post(cycleTerm + *cleanTime == *cycleTime);
// propagating problem
if (problem.propagate()) {
printf("Problem is infeasible\n");
exit(1);
}
// Solve the problem
// creation of the solver
KSolver solver(problem);
// setting objective and sense of optimization
problem.setSense(KProblem::Minimize);
problem.setObjective(*cycleTime);
int result = solver.optimize();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();
// Solution printing
printf("Minimum cycle time: %i\n", sol->getValue(*cycleTime));
printf("Sequence of batches:\nBatch Duration Cleaning\n");
int first=0;
do {
printf("%i\t%i\t%i\n", first, DUR[first],CLEAN[first][sol->getValue(succ[first])]);
first = sol->getValue(succ[first]);
} while (first!=0);
from kalis import *
### Data
# Number of paint batches (=jobs)
nb_jobs = 5
# Durations of jobs
jobs_durations = [40, 35, 45, 32, 50]
# Cleaning times between jobs
jobs_cleaning_times = [[0, 11, 7, 13, 11],
[5, 0, 13, 15, 15],
[13, 15, 0, 23, 11],
[9, 13, 5, 0, 3],
[3, 7, 7, 7, 0]]
### Creation of the problem
# Creation of the Kalis session
session = KSession()
# Creation of the problem in this session
problem = KProblem(session, "B-5 Paint production")
# Setting data as a KIntMatrix
K_cleaning_times_matrix = KIntMatrix(5, 5, 0, "CLEAN")
for i in range(nb_jobs):
for j in range(nb_jobs):
K_cleaning_times_matrix.setMatrix(i, j, jobs_cleaning_times[i][j])
### Variables creation
# Successor of a batch
batch_successor = KIntVarArray()
for j in range(nb_jobs):
batch_successor += KIntVar(problem, "succ(%d)" % j, 0, nb_jobs - 1)
batch_successor[j].remVal(j)
# Cycle time monitoring
clean_time = KIntVar(problem, "cleanTime", 0, 1000)
# Assign values to 'batch_successor' variables as to obtain a single cycle
# 'clean_time' is the sum of the cleaning times
problem.post(KCycle(batch_successor, None, clean_time, K_cleaning_times_matrix))
# Objective variable
cycle_time = KIntVar(problem, "cycleTime", 0, 1000)
problem.post(sum(jobs_durations) + clean_time == cycle_time)
### Solve the problem
# First propagation to check inconsistency
if problem.propagate():
print("Problem is infeasible")
sys.exit(1)
# Set the solver
solver = KSolver(problem)
# Setting objective and sense of optimization
problem.setSense(KProblem.Minimize)
problem.setObjective(cycle_time)
# Run optimization
result = solver.optimize()
# Solution printing
if result:
solution = problem.getSolution()
solution.printResume()
print("Minimum cycle time: %d" % solution.getValue(cycle_time))
print("Sequence of batches:")
print("Batch Duration Cleaning")
j = solution.getValue(batch_successor[0])
while j != 0:
next_job = solution.getValue(batch_successor[j])
print("%d\t%d\t%d" % (j, jobs_durations[j], jobs_cleaning_times[j][next_job]))
j = next_job
// Cleaning times between jobs
KIntMatrix CLEAN = new KIntMatrix(5,5,0,"CLEAN");
CLEAN.setMatrix(0,0,0);
CLEAN.setMatrix(1,0,11);
CLEAN.setMatrix(2,0,7);
CLEAN.setMatrix(3,0,13);
CLEAN.setMatrix(4,0,11);
CLEAN.setMatrix(0,1,5);
CLEAN.setMatrix(1,1,0);
CLEAN.setMatrix(2,1,13);
CLEAN.setMatrix(3,1,15);
CLEAN.setMatrix(4,1,15);
CLEAN.setMatrix(0,2,13);
CLEAN.setMatrix(1,2,15);
CLEAN.setMatrix(2,2,0);
CLEAN.setMatrix(3,2,23);
CLEAN.setMatrix(4,2,11);
CLEAN.setMatrix(0,3,9);
CLEAN.setMatrix(1,3,13);
CLEAN.setMatrix(2,3,5);
CLEAN.setMatrix(3,3,0);
CLEAN.setMatrix(4,3,3);
CLEAN.setMatrix(0,4,3);
CLEAN.setMatrix(1,4,7);
CLEAN.setMatrix(2,4,7);
CLEAN.setMatrix(3,4,7);
CLEAN.setMatrix(4,4,0);
// Successor of a batch
KIntVarArray succ = new KIntVarArray();
// Objective variable
KIntVar cycleTime = new KIntVar();
// Objective variable
KIntVar cleanTime = new KIntVar();
// Creation of the problem in this session
KProblem problem = new KProblem(session,"B-5 Paint production");
// variables creation
int j;
for (j=0; j<NJ; j++)
{
succ.add(new KIntVar(problem, "succ(" + j + ")",0, NJ-1) );
succ.getElt(j).remVal(j);
}
cleanTime = new KIntVar(problem, "cleanTime", 0, 1000);
// Assign values to 'succ' variables as to obtain a single cycle
// 'cleanTime' is the sum of the cleaning times
problem.post(new KCycle(succ, null,cleanTime, CLEAN) );
// objective variable creation
cycleTime = new KIntVar(problem, "cycleTime", 0, 1000);
// Objective: minimize the duration of a production cycle
int sumOfDUR = 0;
for (j=0; j<NJ; j++)
{
sumOfDUR += DUR[j];
}
problem.post(new KGreaterOrEqualXyc(cycleTime, cleanTime, sumOfDUR));
// propagating problem
if (problem.propagate())
{
System.out.println("Problem is infeasible");
exit(1);
}
// Solve the problem
// creation of the solver
KSolver solver = new KSolver(problem);
// setting objective and sense of optimization
problem.setSense(KProblem.Sense.Minimize);
problem.setObjective(cycleTime);
solver.optimize();
// solution printing
KSolution sol = problem.getSolution();
// print solution resume
sol.printResume();
// Solution printing
System.out.println("Minimum cycle time: " + sol.getValue(cycleTime));
System.out.print("Sequence of batches:\nBatch Duration Cleaning\n");
int first=0;
do {
System.out.print(first + "\t" + DUR[first] + "\t" + intp_value(CLEAN.getMatrix(first,sol.getValue(succ.getElt(first)))) + "\n");
first = sol.getValue(succ.getElt(first));
} while (first!=0);
Results¶
The optimal solution to this problem has a minimum cycle time of 243 minutes, resulting from 202 minutes of (incompressible) processing time and 41 minutes of cleaning. The problem statistics produced by Artelys Kalis for a model run reveal that the cycle version of this model is the most efficient way of representing and solving the problem: it takes fewer nodes and a shorter execution time than the two previous versions of the model.
Binary arc-consistency constraint : Euler knight tour¶
Our task is to find a tour on a chessboard for a knight figure such that the knight moves through every cell exactly once and at the end of the tour returns to its starting point. The path of the knight must follow the standard chess rules: a knight moves either one cell vertically and two cells horizontally, or two cells in the vertical and one cell in the horizontal direction, as shown in the following graphic (Fig. 13):
Fig. 13 Permissible moves for a knight¶
Model formulation¶
To represent the chessboard we number the cells from \(0\) to \(N-1\), where \(N\) is the number of cells of the board. The path of the knight is defined by \(N\) variables \(pos_i\) that indicate the ith position of the knight on its tour. The first variable is fixed to zero as the start of the tour. Another obvious constraint we need to state is that all variables \(pos_i\) take different values (every cell of the chessboard is visited exactly once):
We are now left with the necessity to establish a constraint relation that checks whether consecutive positions define a valid knight move. To this aim we define a new binary constraint valid_knight_move that checks whether a given pair of values defines a permissible move according to the chess rules for knight moves. Vertically and horizontally, the two values must be no more than two cells apart and the sum of the vertical and horizontal difference must be equal to three. The complete model then looks as follows.
Implementation¶
Testing whether moving from position a to position b is a valid move for a knight figure can be done with the following function KnightMoveOk() :
bool KnightMoveOk(int a,int b,int S) {
int xa,ya,xb,yb,delta_x,delta_y;
xa = a / S;
ya = a % S;
xb = b / S;
yb = b % S;
delta_x = abs(xa-xb);
delta_y = abs(ya-yb);
return (delta_x<=2) && (delta_y<=2) && (delta_x+delta_y==3);
}
def KnightMoveOk(a: int, b: int, nb_rows: int) -> bool:
xa = a // nb_rows
ya = a % nb_rows
xb = b // nb_rows
yb = b % nb_rows
delta_x = abs(xa - xb)
delta_y = abs(ya - yb)
return (delta_x <= 2) and (delta_y <= 2) and (delta_x + delta_y <= 3)
public boolean KnightMoveOk(int a,int b, int S) {
int xa = a / S;
int ya = a % S;
int xb = b / S;
int yb = b % S;
int delta_x = (xa>xb)? xa-xb : xb - xa;
int delta_y = (ya>yb)? ya-yb : yb - ya;
return delta_x<=2 && delta_y<=2 && delta_x+delta_y==3;
}
The following model defines the user constraint function valid KnightMoveOk as the implementation of the new binary constraints on pairs of \(move_p\) variables (the constraints are established with KACBinTableConstraint).
// Number of rows/columns
int S = 8;
// Total number of cells
int N = S * S;
// Cell at position p in the tour
KIntVarArray pos;
// Creation of the problem in this session
KProblem problem(session,"Euler Knight");
// variables creation
char name[80];
int j,i;
for (j=0;j<N;j++) {
sprintf(name,"pos(%i)",j);
pos += (* new KIntVar( problem,name,0,N-1) );
}
// Fix the start position
pos[0].instantiate(0);
// Each cell is visited once
problem.post(new KAllDifferent("alldiff",pos,KAllDifferent::GENERALIZED_ARC_CONSISTENCY));
// The path of the knight obeys the chess rules for valid knight moves
bool ** tab;
tab = new bool*[N];
int v1,v2;
for (v1=0;v1<N;v1++) {
tab[v1] = new bool[N];
}
for (v1=0;v1<N;v1++) {
for (v2=0;v2<N;v2++) {
tab[v1][v2] = KnightMoveOk(v1,v2,S);
}
}
for (i=0;i<N-1;i++) { problem.post(KACBinTableConstraint(pos[i],pos[i+1],tab,KACBinTableConstraint::ALGORITHM_AC2001,"KnightMove"));
}
// the Knight must return to its first position
problem.post(KACBinTableConstraint(pos[N-1],pos[0],tab,KACBinTableConstraint::ALGORITHM_AC2001,"KnightMove"));
// Setting enumeration parameters
KBranchingSchemeArray myBa;
myBa += KProbe(KSmallestMin(),KMaxToMin(),pos,14);
// Solve the problem
// creation of the solver
KSolver solver(problem,myBa);
// propagating problem
if (problem.propagate()) {
printf("Problem is infeasible\n");
exit(1);
}
int result = solver.solve();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();
for (j=0;j<N;j++) {
printf("%i -> ",sol->getValue(pos[j]));
}
printf("0\n");
from kalis import *
### Data
# Number of rows/columns
nb_rows = 8
# Total number of cells
N = nb_rows * nb_rows
### Variables creation
# Creation of the Kalis session and of the optimization problem
session = KSession()
problem = KProblem(session, "Euler Knight")
# Cell at position p in the tour
positions = KIntVarArray()
for p in range(N):
positions += KIntVar(problem, "pos(%d)" % p, 0, N-1)
### Constraints creation
# Fix the start position
positions[0].instantiate(0)
# Each cell is visited once
problem.post(KAllDifferent("alldiff", positions, KAllDifferent.GENERALIZED_ARC_CONSISTENCY))
# The path of the knight obeys the chess rules for valid knight moves
allowed_moves_table = [[KnightMoveOk(v1, v2, nb_rows) for v2 in range(N)] for v1 in range(N)]
for i in range(N - 1):
problem.post(KACBinTableConstraint(positions[i], positions[i + 1],
allowed_moves_table,
KACBinTableConstraint.ALGORITHM_AC2001,
"KnightMove"))
# The Knight must return to its first position
problem.post(KACBinTableConstraint(positions[N - 1], positions[0],
allowed_moves_table,
KACBinTableConstraint.ALGORITHM_AC2001,
"KnightMove"))
### Solve the problem
# First propagation to check inconsistency
if problem.propagate():
print("Problem is infeasible")
sys.exit(1)
# Setting enumeration parameters
my_branching_array = KBranchingSchemeArray()
my_branching_array += KProbe(KSmallestMin(), KMaxToMin(), positions, 14)
# Set the solver
solver = KSolver(problem, my_branching_array)
# Run optimization
result = solver.solve()
# Solution printing
if result:
solution = problem.getSolution()
solution.printResume()
for i in range(N):
print(solution.getValue(positions[i]), end=" ")
print("0")
//todo
The branching scheme used in this model is the KProbe heuristic, in combination with the variable selection KSmallestMin (choose variable with smallest lower bound) and the value selection criterion KMaxToMin (from largest to smallest domain value). Our model defines one parameter. It is thus possible to change the size of the chessboard (S) when executing the model without having to modify the model source.
Results¶
The first solution printed out by our model is the following tour:
Alternative implementation¶
Whereas the aim of the model above is to give an example of the definition of user constraints, it is possible to implement this problem in a more efficient way using the model developed for the previous cyclic scheduling problem. The set of successors (domains of variables \(succ_p\)) can be calculated using the same algorithm that we have used above in the implementation of the user-defined binary constraints. Without repeating the complete model definition at this place, we simply display the model formulation, including the calculation of the sets of possible successors (procedure calculate_successors, and the modified procedure print_sol for solution printout). We use a simpler version of the cycle constraints than the one we have seen in previous section, its only argument is the set of successor variables as there are no weights to the arcs in this problem.
// Total number of cells
int N = S * S;
// Cell at position p in the tour
KIntVarArray succ;
// Creation of the problem in this session
KProblem problem(session,"Euler Knight 2");
// variables creation
char name[80];
int j,i;
for (j=0;j<N;j++) {
sprintf(name,"succ(%i)",j);
succ += (* new KIntVar( problem,name,0,N-1) );
}
// Calculate set of possible successors
for (j=0;j<N;j++) {
for (i=0;i<N;i++) {
if (!KnightMoveOk(j,i,S)) {
// i is not a possible successor for j
succ[j].remVal(i);
}
}
}
// Each cell is visited once, no subtours
problem.post(new KCycle(&succ,NULL,NULL,NULL));
// Solve the problem
// creation of the solver
KSolver solver(problem);
// propagating problem
if (problem.propagate()) {
printf("Problem is infeasible\n");
exit(1);
}
int result = solver.solve();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();
int thispos=0;
int nextpos=sol->getValue(succ[0]);
while (nextpos!=0) {
printf("%i -> ",thispos);
thispos=nextpos;
nextpos=sol->getValue(succ[thispos]);
}
printf("0\n");
#todo
// Number of rows/columns
int S = 8;
// Total number of cells
int N = S * S;
// Cell at position p in the tour
KIntVarArray succ = new KIntVarArray();
// variables creation
int j, i;
for (j = 0; j < N; j++)
{
succ.add(new KIntVar(problem, "succ(" + j + ")", 0, N - 1));
}
// Calculate set of possible successors
for (j = 0; j < N; j++)
{
for (i = 0; i < N; i++)
{
if (!KnightMoveOk(j, i, S))
{
// i is not a possible successor for j
succ.getElt(j).remVal(i);
}
}
}
// Each cell is visited once, no subtours
problem.post(new KCycle(succ, null, null, null));
// Solve the problem
// creation of the solver
KSolver solver = new KSolver(problem);
// propagating problem
if (problem.propagate())
{
System.out.println("Problem is infeasible");
exit(1);
}
int result = solver.solve();
// solution printing
KSolution sol = problem.getSolution();
// print solution resume
sol.printResume();
int thispos = 0;
int nextpos = sol.getValue(succ.getElt(0));
while (nextpos != 0)
{
System.out.print(thispos + " -> ");
thispos = nextpos;
nextpos = sol.getValue(succ.getElt(thispos));
}
System.out.println("0\n");
The calculation of the domains for the \(succ_p\) variables reduces these to 2-8 elements (as compared to the \(N=64\) values for every \(pos_p\) variables), which clearly reduces the search space for this problem. This second model finds the first solution to the problem after 131 nodes taking just a fraction of a second to execute on a standard PC whereas the first model requires several thousand nodes and considerably longer running times. It is possible to reduce the number of branch-and-bound nodes even further by using yet another version of the cycle constraint that works with successor and predecessor variables. This version of cycle performs a larger amount of propagation, at the expense of (slightly) slower execution times for our problem when S < 8. For S > 8, the computation expense due to the stronger propagation pays. This compromise strength of propagation / nodes explored is typical of hard combinatorial problems where the need of stronger propagation arise for a certain size of the problem. Below this size, a simpler but faster propagation is the best choice. Above this size, the stronger propagation scheme gives the best results and is sometime necessary to find solution in a reasonnable time. As the limit of size for this behavior is problem dependent, the user is therefore encouraged to try both algorithms.

Fig. 14 Graphical representation of a knight’s tour with on a 24x24 chessboard¶
Generalized arc-consistency constraint : Task assignment problem¶
The problem consists in finding a sequence of starting times of various activities, namely \(A,B,C,D,E\), of a given plant. Each activity got 5 different time slots for its starting time, represented by the set \(\{1,2,3,4\}\). Due to some plant requirements, two-by-two constraints exists upon the starting time activities :
B can’t begin at 3 ;
C can’t begin at 2 ;
A and B can’t begin at the same starting time ;
B and C can’t begin at the same starting time ;
C must begin after D ;
E must begin after A ;
E must begin after B ;
E must begin after C ;
E must begin after D ;
B and D can’t begin at the same starting time ;
A and D must begin at the same time.
Model formulation¶
To represent the activities starting time we defined as many variables as activities \(tasks_A, tasks_B, tasks_C, tasks_D, tasks_E\), with a domain of integer from \(\{1,2,3,4\}\). Constraints can be expressed as implicit constraints but also through a global constraint : a generic arc-consistency (GAC) constraint. It mainly proceeds by examining the arcs between tuples of variables and removes those values from its domain which aren’t consistent with the constraint.
The implicit constraints can be written as :
And they can be expressed through a test function that validate or not a given starting time combination:
bool StartingTimeCombinationOk(int a, int b, int c, int d, int e) {
return (b!=3) && (c!=2) && (a!=b) && (b!=c) && (c<d) && (a=d) && (e<a) && (e<b) && (e<c) && (e<d) && (b!=d);
}
#todo
// todo
The GAC constraint can be implemented through both classes KGeneralizedArcConsistencyConstraint and KGeneralizedArcConsistencyTableConstraint. Difference relies on the way the test function is used in the implementation of the constraint, and therefore the propagation algorithm behind.
Implementation of the GAC constraint¶
In the standard version of the GAC constraint, end-user needs to create a derived class of KGeneralizedArcConsistencyConstraint which mainly overloads the testIfSatisfied() (constructor and copy-constructor are also needed). The former method is used by the propagation engine to test all valid combinations defined by the domain of variables. testIfSatisfied() is called each time one tuple needs to be validated.
class StartingTimeCombination : public KGeneralizedArcConsistencyConstraint {
public:
KIntVarArray _vars;
StartingTimeCombination(KIntVarArray& vars)
: KGeneralizedArcConsistencyConstraint(vars,GENERALIZED_ARC_CONSISTENCY, "StartingTimeCombinationGAC"),_vars(vars)
{}
~StartingTimeCombination() {
}
bool testIfSatisfied(int * vals)
{
int _a = vals[1];int _b = vals[2];int _c = vals[3];int _d = vals[4];int _e = vals[5];
return StartingTimeCombinationOk(_a, _b, _c, _d, _e);
}
StartingTimeCombination(const StartingTimeCombination& toCopy) : KGeneralizedArcConsistencyConstraint(toCopy)
{
_vars = KIntVarArray(toCopy._vars);
}
};
#todo
// todo
Finally the complete task assignment example implementation is :
class StartingTimeCombination : public KGeneralizedArcConsistencyConstraint {
public:
KIntVarArray _vars;
StartingTimeCombination(KIntVarArray& vars)
: KGeneralizedArcConsistencyConstraint(vars,GENERALIZED_ARC_CONSISTENCY, "StartingTimeCombinationGAC"),_vars(vars)
{}
~StartingTimeCombination() {
}
bool testIfSatisfied(int * vals)
{
int _a = vals[1];int _b = vals[2];int _c = vals[3];int _d = vals[4];int _e = vals[5];
return StartingTimeCombinationOk(_a, _b, _c, _d, _e);
}
StartingTimeCombination(const StartingTimeCombination& toCopy) : KGeneralizedArcConsistencyConstraint(toCopy)
{
_vars = KIntVarArray(toCopy._vars);
}
};
/////////////////////////////////////////////
// Task activities starting time
/////////////////////////////////////////////
enum TASKS {A,B,C,D,E};
const char * TaskName[] = {"A","B","C","D","E"};
int N=5;
KIntVarArray tasks;
/////////////////////////////////////////////
// Create the task activities variables
/////////////////////////////////////////////
char name[80];
int indexTask;
for (indexTask = A; indexTask <= E; indexTask++) {
sprintf(name,"task[%s]",TaskName[indexTask]);
tasks += KIntVar(problem,name,1,4);
}
///////////////////////////////////////////////
// the task activities should follow the combination rules
///////////////////////////////////////////////
StartingTimeCombination gacConstraint(tasks);
problem.post(gacConstraint);
/////////////////////////////////////////////
// Solve the problem
// creation of the solver
/////////////////////////////////////////////
KSolver solver(problem);
/////////////////////////////////////////////
// propagating problem
/////////////////////////////////////////////
if (problem.propagate()) {
printf("Problem is infeasible\n");
return 1;
}
solver.solve();
/////////////////////////////////////////////
// solution printing
/////////////////////////////////////////////
KSolution * sol = &problem.getSolution();
/////////////////////////////////////////////
// print solution resume
/////////////////////////////////////////////
sol->printResume();
cout << "### Computation time = " << solver.getDblAttrib(KSolver::ComputationTime) << endl;
cout << "### Number of nodes = " << solver.getIntAttrib(KSolver::NumberOfNodes) << endl;
cout << "### Depth = " << solver.getIntAttrib(KSolver::Depth) << endl;
return 0;
}
#todo
// todo
Implementation of the GAC Table constraint¶
In the following GAC constraint (KGeneralizedArcConsistencyTableConstraint version), end-user needs this time to enumerate the complete list of valid tuples that defined the valid support of the variables with respect to the constraint. This list of tuple will be used by the propagation engine to filter the domain variables, as it is done with testIfSatisfied() in KGeneralizedArcConsistencyConstraint. This implementation is identified as the one to be preferred when the list of valid tuples is greatly inferior to the overall combinatorial of the variables.
The implementation is:
/////////////////////////////////////////////
// Task activities starting time
/////////////////////////////////////////////
enum TASKS {A,B,C,D,E};
const char * TaskName[] = {"A","B","C","D","E"};
int N=5;
KIntVarArray tasks;
/////////////////////////////////////////////
// Create the task activities variables
/////////////////////////////////////////////
char name[80];
int indexTask;
for (indexTask = A; indexTask <= E; indexTask++) {
sprintf(name,"task[%s]",TaskName[indexTask]);
tasks += KIntVar(problem,name,1,4);
}
///////////////////////////////////////////////
// the task activities should follow the combination rules
///////////////////////////////////////////////
KTupleArray tuple;
int _a, _b, _c, _d, _e;
for (_a = 0; _a <= 4; _a++) for (_b = 0; _b <= 4; _b++) for (_c = 0; _c <= 4; _c++) for (_d = 0; _d <= 4; _d++) for (_e = 0; _e <= 4; _e++) {
if (StartingTimeCombinationOk(_a, _b, _c, _d, _e)) {
KIntArray tuple_elem(N);
tuple_elem[A] = _a; tuple_elem[B] = _b; tuple_elem[C] = _c; tuple_elem[D] = _d; tuple_elem[E] = _e;
tuple.add(tuple_elem);
}
}
KGeneralizedArcConsistencyTableConstraint gacTableConstraint(tasks, tuple,"StartingTimeCombinationGACTable");
problem.post(gacTableConstraint);
/////////////////////////////////////////////
// Solve the problem
// creation of the solver
/////////////////////////////////////////////
KSolver solver(problem);
/////////////////////////////////////////////
// propagating problem
/////////////////////////////////////////////
if (problem.propagate()) {
printf("Problem is infeasible\n");
return 1;
}
solver.solve();
/////////////////////////////////////////////
// solution printing
/////////////////////////////////////////////
KSolution * sol = &problem.getSolution();
/////////////////////////////////////////////
// print solution resume
/////////////////////////////////////////////
sol->printResume();
cout << "### Computation time = " << solver.getDblAttrib(KSolver::ComputationTime) << endl;
cout << "### Number of nodes = " << solver.getIntAttrib(KSolver::NumberOfNodes) << endl;
cout << "### Depth = " << solver.getIntAttrib(KSolver::Depth) << endl;
return 0;
#todo
// todo

