Complementarity constraints
A complementarity constraint enforces that two variables are complementary to each other; i.e., that the following conditions hold for scalar variables x and y:
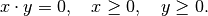
The condition above is sometimes expressed more compactly as

Intuitively, a complementarity constraint is a way to model a constraint that is combinatorial in nature since, for example, the complementary conditions imply that either x or y must be 0 (both may be 0 as well).
Without special care, these types of constraints may cause problems for nonlinear optimization solvers because problems that contain these types of constraints fail to satisfy constraint qualifications that are often assumed in the theory and design of algorithms for nonlinear optimization. For this reason, we provide a special interface in Knitro for specifying complementarity constraints. In this way, Knitro can recognize these constraints and handle them with special care internally.
Note
The complementarity features of Knitro may not be available through all interfaces. If a modeling language/interface does not allow you to specifically identify and express complementarity constraints, then these constraints must be formulated as regular constraints and Knitro will not perform any specializations.
Note
There are various ways to express complementarity conditions, but the complementarity features in the Knitro callable library API and MATLAB API require you to specify the complementarity condition as two non-negative variables complementary to each other as shown above. Any complementarity condition can be written in this form.
Example
This problem is taken from J.F. Bard, Convex two-level optimization, Mathematical Programming 40(1), 15-27, 1988.
Assume we want to solve the following MPEC with Knitro.
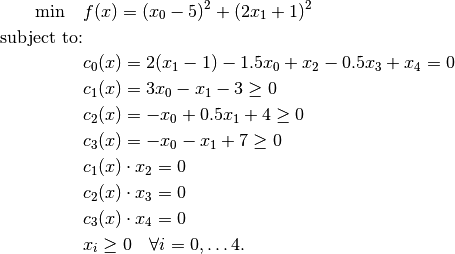
Observe that complementarity constraints appear. Expressing this in compact notation, we have:
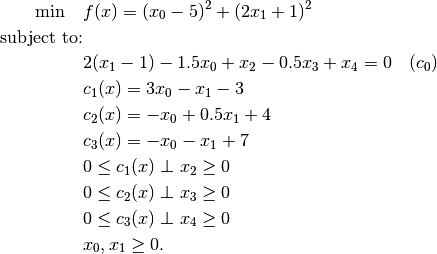
Since Knitro requires that complementarity constraints be
written as two variables complementary to each other, we must
introduce slack variables 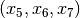 and re-write
the problem as follows:
and re-write
the problem as follows:
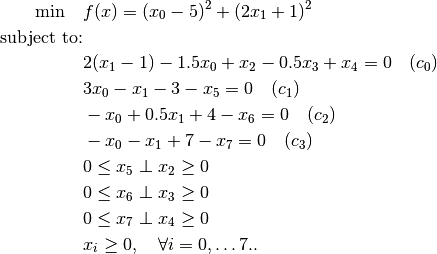
The problem is now in a form suitable for Knitro.
Complementarity constraints in AMPL
Complementarity constraints should be modeled using the AMPL complements command; e.g.,:
0 <= x complements y => 0;
The Knitro callable library API and MATLAB API require that complementarity constraints be formulated as one variable complementary to another variable (both non-negative). However, in AMPL, you can express the complementarity constraints in any form allowed by AMPL. AMPL will then translate the complementarity constraints automatically to the form required by Knitro.
Be aware that the AMPL presolver sometimes removes complementarity constraints. Check carefully that the problem definition reported by Knitro includes all complementarity constraints, or switch off the AMPL presolver by setting option presolve to 0, if you don’t want the AMPL presolver to modify the problem.
Complementarity constraints in MATLAB
Complementarity constraints can be specified through two fields of the extendedFeatures structure. The fields ccIndexList1 and ccIndexList2 contain the pairs of indices of variables that are complementary to each other.
Note
Variables which are specified as complementary should be specified to have a lower bound of 0 through the variable lower bound array lb.
Complementarity constraints with the callable library
Complementarity constraints can be specified in Knitro through a call to the
function KN_add_compcons() which has the following prototype:
int KNITRO_API KN_add_compcons ( KN_context_ptr kc,
const KNINT nCC,
const int * const ccTypes,
const KNINT * const indexComps1,
const KNINT * const indexComps2,
KNINT * const indexCompCons);
In addition to kc, which is a pointer to a structure that holds all the relevant information about a particular problem instance, the arguments are:
nCC, the number of complementarity constraints to be added to the problem (i.e., the number of pairs of variables that are complementary to each other).
ccTypes, array of length nCC specifying the type for each complementarity constraint. Currently this MUST be set to
KN_CCTYPE_VARVARsince Knitro currently only supports complementarity constraints between two (non-negative) variables. However, this parameter will be used in the future to support more general types of complementarities (such as complementarities between a variable and a constraint).indexComps1 and indexComps2, two arrays of length nCC specifying the variable indices for the first and second sets of variables in the pairs of complementary variables.
indexCompCons may be set to NULL. Otherwise, on return it holds the global indices associated with the complementarity constraints that were added (indices are typically allocated sequentially).
Note
Variables which are specified as complementary
through the special KN_add_compcons() functions should be
specified to have a lower bound of 0 through the Knitro lower
bound array xLoBnds.
Complementarity constraints with the object-oriented interface
Complementarity constraints can be specified in the object-oriented interface
by defining the constraints in a class inheriting
from KNProblem.
The KNProblem should call the functions:
setCompConstraintsParts(indexList1, indexList2);
Parameters
indexList1 and indexList2, which have the same length,
specify the variable indices for the first and second sets of variables
in the pairs of complementary variables, example:
// x2 x3 and x4 complements respectively x5, x6 and x7
setCompConstraintsParts({{2, 3, 4}, {5, 6, 7}});
Note
Variables which are specified as complementary should have a lower bound of 0.
This can be set using KNProblem::setVarLoBnds().
AMPL example
The AMPL model for our toy problem above is the following.
# Variables
var x{j in 0..7} >= 0;
# Objective function
minimize obj:
(x[0]-5)^2 + (2*x[1]+1)^2;
# Constraints
s.t. c0: 2*(x[1]-1) - 1.5*x[0] + x[2] - 0.5*x[3] + x[4] = 0;
s.t. c1: 3*x[0] - x[1] - 3 - x[5] = 0;
s.t. c2: -x[0] + 0.5*x[1] + 4 - x[6] = 0;
s.t. c3: -x[0] - x[1] + 7 - x[7] = 0;
s.t. c4: 0 <= x[5] complements x[2] >= 0;
s.t. c5: 0 <= x[6] complements x[3] >= 0;
s.t. c6: 0 <= x[7] complements x[4] >= 0;
Running it through AMPL, we get the following output.
=======================================
Commercial License
Artelys Knitro 15.0.0
=======================================
No start point provided -- Knitro computing one.
Knitro presolve eliminated 0 variables and 0 constraints.
concurrent_evals: 0
datacheck: 0
hessian_no_f: 1
The problem is identified as an MPEC.
Problem Characteristics ( Presolved)
-----------------------
Objective goal: Minimize
Objective type: quadratic
Number of variables: 11 ( 11)
bounded below only: 11 ( 11)
bounded above only: 0 ( 0)
bounded below and above: 0 ( 0)
fixed: 0 ( 0)
free: 0 ( 0)
Number of constraints: 7 ( 7)
linear equalities: 7 ( 7)
quadratic equalities: 0 ( 0)
gen. nonlinear equalities: 0 ( 0)
linear one-sided inequalities: 0 ( 0)
quadratic one-sided inequalities: 0 ( 0)
gen. nonlinear one-sided inequalities: 0 ( 0)
linear two-sided inequalities: 0 ( 0)
quadratic two-sided inequalities: 0 ( 0)
gen. nonlinear two-sided inequalities: 0 ( 0)
Number of complementarities: 3 ( 3)
Number of nonzeros in Jacobian: 20 ( 20)
Number of nonzeros in Hessian: 2 ( 2)
Knitro using the Interior-Point/Barrier Direct algorithm.
Iter Objective FeasError OptError ||Step|| CGits
-------- -------------- ---------- ---------- ---------- -------
0 2.811162e+01 1.548e+00
10 1.700000e+01 6.178e-10 4.001e-07 3.202e-05 0
EXIT: Locally optimal solution found.
Final Statistics
----------------
Final objective value = 1.70000000199027e+01
Final feasibility error (abs / rel) = 6.18e-10 / 3.99e-10
Final optimality error (abs / rel) = 4.00e-07 / 5.00e-08
# of iterations = 10
# of CG iterations = 1
# of function evaluations = 0
# of gradient evaluations = 0
# of Hessian evaluations = 0
Total program time (secs) = 0.00268 ( 0.002 CPU time)
Time spent in evaluations (secs) = 0.00000
===============================================================================
Knitro 15.0.0: Locally optimal or satisfactory solution.
objective 17.000000019902657; feasibility error 6.18e-10
10 iterations; 0 function evaluations
Knitro received our three complementarity constraints correctly (“Number of complementarities: 3”) and converged successfully (“Locally optimal solution found”).
MATLAB example
The following functions can be used in MATLAB to solve the same example as is shown for AMPL.
function exampleMPEC1
Jpattern = [];
Hpattern = sparse(zeros(8));
Hpattern(1,1) = 1;
Hpattern(2,2) = 1;
extendedFeatures.JacobPattern = Jpattern;
extendedFeatures.HessPattern = Hpattern;
extendedFeatures.HessFcn = @hessfun;
options = knitro_options('algorithm',1,'outlev',4, ...
'gradopt',1,'hessopt',1,'maxit',1000, ...
'feastol',1e-8,'opttol',1e-8);
A = []; b = [];
Aeq = [-1.5 2 1 -0.5 1 0 0 0;
3 -1 0 0 0 -1 0 0;
-1 0.5 0 0 0 0 -1 0;
-1 -1 0 0 0 0 0 -1];
beq = [2 3 -4 -7];
lb = zeros(8,1);
ub = Inf*ones(8,1);
x0 = zeros(8,1);
extendedFeatures.ccIndexList1 = [6 7 8];
extendedFeatures.ccIndexList2 = [3 4 5];
[x,fval,exitflag,output,lambda] = ...
knitro_nlp(@objfun,x0,A,b,Aeq,beq,lb,ub,@constfun,extendedFeatures,options);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [f,g] = objfun(x)
f = (x(1)-5)^2 + (2*x(2)+1)^2;
if nargout > 1
g = zeros(8,1);
g(1) = 2*(x(1)-5);
g(2) = 4*(2*x(2)+1);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [c,ceq,Gc,Gceq]= constfun(x)
c = [];
ceq=[];
Gc = [];
Gceq=[];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [H]= hessfun(x,lambda)
H=sparse(zeros(8));
H(1,1) = 2;
H(2,2) = 4;
Running this file will produce the following output from Knitro.
=======================================
Commercial License
Artelys Knitro 15.0.0
=======================================
Knitro presolve eliminated 0 variables and 0 constraints.
algorithm: 1
concurrent_evals: 0
feastol: 1e-08
honorbnds: 1
maxit: 1000
opttol: 1e-08
outlev: 4
The problem is identified as an MPEC.
Knitro changing bar_initpt from AUTO to 3.
Knitro changing bar_murule from AUTO to 4.
Knitro changing bar_penaltycons from AUTO to 1.
Knitro changing bar_penaltyrule from AUTO to 2.
Knitro changing bar_switchrule from AUTO to 1.
Knitro changing linsolver from AUTO to 2.
Knitro shifted start point to satisfy presolved bounds (8 variables).
Problem Characteristics ( Presolved)
-----------------------
Objective goal: Minimize
Objective type: general
Number of variables: 8 ( 8)
bounded below only: 8 ( 8)
bounded above only: 0 ( 0)
bounded below and above: 0 ( 0)
fixed: 0 ( 0)
free: 0 ( 0)
Number of constraints: 4 ( 4)
linear equalities: 4 ( 4)
quadratic equalities: 0 ( 0)
gen. nonlinear equalities: 0 ( 0)
linear one-sided inequalities: 0 ( 0)
quadratic one-sided inequalities: 0 ( 0)
gen. nonlinear one-sided inequalities: 0 ( 0)
linear two-sided inequalities: 0 ( 0)
quadratic two-sided inequalities: 0 ( 0)
gen. nonlinear two-sided inequalities: 0 ( 0)
Number of complementarities: 3 ( 3)
Number of nonzeros in Jacobian: 14 ( 14)
Number of nonzeros in Hessian: 2 ( 2)
Knitro using the Interior-Point/Barrier Direct algorithm.
Iter fCount Objective FeasError OptError ||Step|| CGits
-------- -------- -------------- ---------- ---------- ---------- -------
0 2 2.496050e+01 4.030e+00
1 3 2.847389e+01 1.748e+00 2.160e+00 1.990e+00 1
2 4 4.226663e+01 3.832e-01 4.643e+00 1.442e+00 0
3 5 4.667799e+01 1.126e-02 3.638e+00 5.993e-01 0
4 6 4.213217e+01 4.179e-03 1.258e+01 1.185e+00 0
5 7 4.074018e+01 3.072e-03 1.265e+01 1.580e-01 1
6 8 3.810894e+01 1.133e-04 1.259e+01 3.113e-01 0
7 9 1.701407e+01 1.682e-04 1.542e+00 4.771e+00 0
8 10 1.699966e+01 1.522e-04 6.416e-02 2.385e-02 0
9 11 1.700003e+01 1.799e-06 3.532e-05 2.154e-04 0
10 12 1.700000e+01 6.354e-11 1.530e-09 5.298e-05 0
EXIT: Locally optimal solution found.
Final Statistics
----------------
Final objective value = 1.70000000010379e+01
Final feasibility error (abs / rel) = 6.35e-11 / 1.58e-11
Final optimality error (abs / rel) = 1.53e-09 / 1.91e-10
# of iterations = 10
# of CG iterations = 2
# of function evaluations = 12
# of gradient evaluations = 12
# of Hessian evaluations = 10
Total program time (secs) = 0.00827 ( 0.019 CPU time)
Time spent in evaluations (secs) = 0.00464
===============================================================================
C example
The same example can be implemented using the callable library.
Arrays indexList1 and indexList2 are used to specify the list of
complementarities and the KN_add_compcons() function is called to
register the list.
#include <stdio.h>
#include <stdlib.h>
#include "knitro.h"
int main (int argc, char *argv[])
{
int i, nStatus, error;
/** Declare variables. */
KN_context *kc;
int n, m;
double xLoBnds[8] = {0, 0, 0, 0, 0, 0, 0};
double xInitVals[8] = {0, 0, 0, 0, 0, 0, 0};
double cEqBnds[4] = {2, 3, -4, -7};
/** Used to define linear constraints. */
int lconIndexCons[14];
int lconIndexVars[14];
double lconCoefs[14];
/** Used to specify linear objective terms. */
int lobjIndexVars[2];
double lobjCoefs[2];
/** Used to specify quadratic objective terms. */
int qobjIndexVars1[2];
int qobjIndexVars2[2];
double qobjCoefs[2];
/** Used to specify complementarity constraints. */
int ccTypes[3] = {KN_CCTYPE_VARVAR, KN_CCTYPE_VARVAR, KN_CCTYPE_VARVAR};
int indexComps1[3] = {2, 3, 4};
int indexComps2[3] = {5, 6, 7};
/** Solution information */
double x[8];
double objSol;
double feasError, optError;
/** Create a new Knitro solver instance. */
error = KN_new(&kc);
if (error) exit(-1);
if (kc == NULL)
{
printf ("Failed to find a valid license.\n");
return( -1 );
}
/** Initialize Knitro with the problem definition. */
/** Add the variables and set their bounds and initial values.
* Note: unset bounds assumed to be infinite. */
n = 8;
error = KN_add_vars(kc, n, NULL);
if (error) exit(-1);
error = KN_set_var_lobnds_all(kc, xLoBnds);
if (error) exit(-1);
error = KN_set_var_primal_init_values_all(kc, xInitVals);
if (error) exit(-1);
/** Add the constraints and set their bounds. */
m = 4;
error = KN_add_cons(kc, m, NULL);
if (error) exit(-1);
error = KN_set_con_eqbnds_all(kc, cEqBnds);
if (error) exit(-1);
/** Add coefficients for all linear constraints at once. */
/** c0 */
lconIndexCons[0]=0; lconIndexVars[0]=0; lconCoefs[0]=-1.5;
lconIndexCons[1]=0; lconIndexVars[1]=1; lconCoefs[1]=2.0;
lconIndexCons[2]=0; lconIndexVars[2]=2; lconCoefs[2]=1.0;
lconIndexCons[3]=0; lconIndexVars[3]=3; lconCoefs[3]=-0.5;
lconIndexCons[4]=0; lconIndexVars[4]=4; lconCoefs[4]=1.0;
/** c1 */
lconIndexCons[5]=1; lconIndexVars[5]=0; lconCoefs[5]=3.0;
lconIndexCons[6]=1; lconIndexVars[6]=1; lconCoefs[6]=-1.0;
lconIndexCons[7]=1; lconIndexVars[7]=5; lconCoefs[7]=-1.0;
/** c2 */
lconIndexCons[8]=2; lconIndexVars[8]=0; lconCoefs[8]=-1.0;
lconIndexCons[9]=2; lconIndexVars[9]=1; lconCoefs[9]=0.5;
lconIndexCons[10]=2; lconIndexVars[10]=6; lconCoefs[10]=-1.0;
/** c3 */
lconIndexCons[11]=3; lconIndexVars[11]=0; lconCoefs[11]=-1.0;
lconIndexCons[12]=3; lconIndexVars[12]=1; lconCoefs[12]=-1.0;
lconIndexCons[13]=3; lconIndexVars[13]=7; lconCoefs[13]=-1.0;
error = KN_add_con_linear_struct (kc, 14, lconIndexCons, lconIndexVars,
lconCoefs);
if (error) exit(-1);
/** Note that the objective (x0 - 5)^2 + (2 x1 + 1)^2 when
* expanded becomes:
* x0^2 + 4 x1^2 - 10 x0 + 4 x1 + 26 */
/** Add quadratic coefficients for the objective */
qobjIndexVars1[0]=0; qobjIndexVars2[0]=0; qobjCoefs[0]=1.0;
qobjIndexVars1[1]=1; qobjIndexVars2[1]=1; qobjCoefs[1]=4.0;
error = KN_add_obj_quadratic_struct (kc, 2, qobjIndexVars1,
qobjIndexVars2, qobjCoefs);
if (error) exit(-1);
/** Add linear coefficients for the objective */
lobjIndexVars[0]=0; lobjCoefs[0]=-10.0;
lobjIndexVars[1]=1; lobjCoefs[1]=4.0;
error = KN_add_obj_linear_struct (kc, 2,
lobjIndexVars, lobjCoefs);
if (error) exit(-1);
/** Add constant to the objective */
error = KN_add_obj_constant (kc, 26.0);
if (error) exit(-1);
/** Set minimize or maximize (if not set, assumed minimize) */
error = KN_set_obj_goal(kc, KN_OBJGOAL_MINIMIZE);
if (error) exit(-1);
/** Now add the complementarity constraints */
error = KN_add_compcons (kc, 3, ccTypes, indexComps1, indexComps2, NULL);
if (error) exit(-1);
/** Solve the problem.
*
* Return status codes are defined in "knitro.h" and described
* in the Knitro manual. */
nStatus = KN_solve (kc);
/** Delete the Knitro solver instance. */
KN_free (&kc);
return( 0 );
}
Running this code produces an output similar to what we obtained with AMPL.
C++ example
Here we look at the C++ equivalent of exampleMPEC1.c.
/*++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
* This example demonstrates how to use Knitro to solve the following
* simple mathematical program with equilibrium/complementarity
* constraints (MPEC/MPCC).
*
* min (x0 - 5)^2 + (2 x1 + 1)^2
* s.t. -1.5 x0 + 2 x1 + x2 - 0.5 x3 + x4 = 2
* x2 complements (3 x0 - x1 - 3)
* x3 complements (-x0 + 0.5 x1 + 4)
* x4 complements (-x0 - x1 + 7)
* x0, x1, x2, x3, x4 >= 0
*
* The complementarity constraints must be converted so that one
* nonnegative variable complements another nonnegative variable.
*
* min (x0 - 5)^2 + (2 x1 + 1)^2
* s.t. -1.5 x0 + 2 x1 + x2 - 0.5 x3 + x4 = 2 (c0)
* 3 x0 - x1 - 3 - x5 = 0 (c1)
* -x0 + 0.5 x1 + 4 - x6 = 0 (c2)
* -x0 - x1 + 7 - x7 = 0 (c3)
* x2 complements x5
* x3 complements x6
* x4 complements x7
* x0, x1, x2, x3, x4, x5, x6, x7 >= 0
*
* The solution is (1, 0, 3.5, 0, 0, 0, 3, 6), with objective value 17.
*++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*/
#include "KNSolver.h"
#include "KNProblem.h"
using namespace knitro;
class ProblemMPEC1 : public knitro::KNProblem {
public:
ProblemMPEC1() : KNProblem(8,4) {
// Variables
this->setVarLoBnds({{0, 0, 0, 0, 0, 0, 0, 0}});
this->setXInitial({{0, 0, 0, 0, 0, 0, 0, 0}});
// Constraints
this->setConEqBnds({{2, 3, -4, -7}});
this->setCompConTypes({{KN_CCTYPE_VARVAR, KN_CCTYPE_VARVAR, KN_CCTYPE_VARVAR}});
// x2 x3 and x4 complements respectively x5, x6 and x7
this->setCompConstraintsParts({{2, 3, 4}, {5, 6, 7}});
// Objective structure
/** Note that the objective (x0 - 5)^2 + (2 x1 + 1)^2 when
* expanded becomes:
* x0^2 + 4 x1^2 - 10 x0 + 4 x1 + 26 */
/** Add quadratic coefficients for the objective */
this->setObjectiveQuadraticPart({ {0,1}, {0,1}, {1.0,4.0} });
/** Add linear coefficients for the objective */
this->setObjectiveLinearPart({ {0,1}, {-10.0,4.0} });
/** Add constant to the objective */
this->setObjConstPart(26.0);
// Constraints Strucutres
/** c0 */
this->getConstraintsLinearParts().add(0 ,{ {0,1,2,3,4}, {-1.5,2.0,1.0,-0.5,1.0} });
/** c1 */
this->getConstraintsLinearParts().add(1 ,{ {0,1,5}, {3.0,-1.0,-1.0} });
/** c2 */
this->getConstraintsLinearParts().add(2 ,{ {0,1,6}, {-1.0,0.5,-1.0} });
/** c3 */
this->getConstraintsLinearParts().add(3 ,{ {0,1,7}, {-1.0,-1.0,-1.0} });
}
};
int main() {
// Create a problem instance.
ProblemMPEC1 instance = ProblemMPEC1();
// Create a solver
knitro::KNSolver solver(&instance);
solver.initProblem();
int solveStatus = solver.solve();
std::vector<double> x;
std::vector<double> lambda;
int nStatus = solver.getSolution(x, lambda);
printf ("\n\n");
printf ("Knitro converged with final status = %d\n", nStatus);
printf (" optimal objective value = %e\n", solver.getObjValue());
printf (" optimal primal values x0=%e\n", x[0]);
printf (" x1=%e\n", x[1]);
printf (" x2=%e complements x5=%e\n", x[2],x[5]);
printf (" x3=%e complements x6=%e\n", x[3],x[6]);
printf (" x4=%e complements x7=%e\n", x[4],x[7]);
printf (" feasibility violation = %e\n", solver.getAbsFeasError());
printf (" KKT optimality violation = %e\n", solver.getAbsOptError());
return 0;
}
Running this file will produce the following output from Knitro.
=======================================
Commercial License
Artelys Knitro 15.0.0
=======================================
Knitro presolve eliminated 0 variables and 0 constraints.
The problem is identified as an MPEC.
Knitro shifted start point further inside presolved bounds (8 variables).
Problem Characteristics ( Presolved)
-----------------------
Objective goal: Minimize
Objective type: quadratic
Number of variables: 8 ( 8)
bounded below only: 8 ( 8)
bounded above only: 0 ( 0)
bounded below and above: 0 ( 0)
fixed: 0 ( 0)
free: 0 ( 0)
Number of constraints: 4 ( 4)
linear equalities: 4 ( 4)
quadratic equalities: 0 ( 0)
gen. nonlinear equalities: 0 ( 0)
linear one-sided inequalities: 0 ( 0)
quadratic one-sided inequalities: 0 ( 0)
gen. nonlinear one-sided inequalities: 0 ( 0)
linear two-sided inequalities: 0 ( 0)
quadratic two-sided inequalities: 0 ( 0)
gen. nonlinear two-sided inequalities: 0 ( 0)
Number of complementarities: 3 ( 3)
Number of nonzeros in Jacobian: 14 ( 14)
Number of nonzeros in Hessian: 2 ( 2)
Knitro using the Interior-Point/Barrier Direct algorithm.
Iter Objective FeasError OptError ||Step|| CGits
-------- -------------- ---------- ---------- ---------- -------
0 2.496050e+01 4.030e+00
10 1.700000e+01 9.391e-13 1.230e-10 2.484e-05 0
EXIT: Locally optimal solution found.
Final Statistics
----------------
Final objective value = 1.70000000001614e+01
Final feasibility error (abs / rel) = 9.39e-13 / 2.33e-13
Final optimality error (abs / rel) = 1.23e-10 / 1.54e-11
# of iterations = 10
# of CG iterations = 2
# of function evaluations = 0
# of gradient evaluations = 0
# of Hessian evaluations = 0
Total program time (secs) = 0.00906 ( 0.004 CPU time)
Time spent in evaluations (secs) = 0.00000
===============================================================================
Knitro converged with final status = 0
optimal objective value = 1.700000e+01
optimal primal values x0=1.000000e+00
x1=1.227320e-10
x2=3.500000e+00 complements x5=8.362969e-13
x3=7.241657e-13 complements x6=3.000000e+00
x4=9.390582e-13 complements x7=6.000000e+00
feasibility violation = 9.390582e-13
KKT optimality violation = 1.230191e-10