File Formats¶
Knitro can import and export optimization problems from several standard file formats. This section provides a detailed guide on each supported format and how Knitro parses them.
LP Format¶
Knitro can import linear and quadratic optimization problems for the standard LP (Linear Programming) file format. LP files should be ASCII-encoded text files.
Basic Structure¶
An LP file is structured into several sections, each identified by a case-insensitive keyword.
MINIMIZE or MAXIMIZE: Defines the objective function.
SUBJECT TO (or ST): Lists the constraints.
BOUNDS: Sets variable bounds (optional).
BINARY: Declares binary variables (optional).
INTEGER: Declares integer variables (optional).
RANGES: Specifies range constraints (optional).
END: Marks the end of the file.
Example¶
Here is a simple example illustrating the structure of an LP file:
MINIMIZE
cost: x + 4 y + 9 z
SUBJECT TO
constraint1: x + y <= 5
constraint2: x + z >= 10
constraint3: y - z = 7
BOUNDS
0 <= x <= 4
-1 <= y <= 1
z free
END
Objective Function Section¶
To include an objective function, the LP file must contain this section, which starts with a keyword such as MINIMIZE, MAXIMIZE, MIN, or MAX. This is followed by an optional label and the objective expression itself.
MINIMIZE
[label:] expression
The objective expression can be a combination of constant terms and linear terms (e.g., coeff * var). If a variable appears without a coefficient, the coefficient is assumed to be 1.
MINIMIZE
cost: 2 x + 3.5 y - z + 10
MAXIMIZE
profit: revenue - expenses
Constraints Section¶
The constraints section follows the objective and begins with a keyword like SUBJECT TO, ST, SUCH THAT, or S.T.. Each constraint is defined on a new line with the following format:
[label:] expression relation rhs
Where:
label: An optional name for the constraint.
expression: A linear combination of variables.
relation: One of<=,>=, or=.
rhs: The numerical right-hand side value.
SUBJECT TO
capacity: 2 x + 3 y <= 100
demand: x + y >= 50
balance: x - y = 0
c4: 0.5 a + 1.2 b + 0.8 c <= 75.5
Variable Bounds Section¶
The optional BOUNDS (or BOUND) section allows you to define lower and upper limits for variables. If a variable’s bounds are not specified, it is treated as unbounded (free), ranging from negative to positive infinity.
Bounds can be specified in several ways:
lower <= variable <= upper
variable >= lower
variable <= upper
variable = value
variable free
The keyword free explicitly declares a variable as unbounded.
BOUNDS
0 <= x <= 100
y >= -50
z <= 25
w = 10
v free
Declaring Variable Types¶
Binary Variables¶
To declare binary variables, list them in the BINARY section (also BIN or BINARIES).
BINARY
x1 x2 x3
Integer Variables¶
To declare general integer variables, list them under the INTEGER section. Synonyms like INT, INTEGERS, GENERAL, GENERALS, or GEN are also accepted.
INTEGER
y1 y2 y3
Complete Example¶
This example combines multiple sections, including variable type declarations:
MINIMIZE
objective: 3 x + 2 y + z
SUBJECT TO
resource1: 2 x + y <= 100
resource2: x + 3 y + z <= 150
demand: x + y >= 25
BOUNDS
x >= 0
0 <= y <= 50
z free
BINARY
x
INTEGER
y
END
Range Constraints Section¶
The optional RANGES (or RANGE) section modifies existing constraints to create double-sided inequalities, effectively placing the constraint’s expression within an interval.
Each line in the RANGES section references a constraint by its label and provides a new lower and upper bound for its expression.
lhs <= constraint_label <= rhs
For example, consider these initial constraints:
SUBJECT TO
con1: x + y <= 10
con2: 2 x + 3 y >= 15
You can apply ranges to them as follows:
RANGES
5 <= con1 <= 10
15 <= con2 <= 25
This effectively transforms the original constraints into:
For
con1:5 <= x + y <= 10For
con2:15 <= 2 x + 3 y <= 25
Note that the bounds specified in the RANGES section can override the original bounds of the referenced constraints. The lower bound will replace the original lower bound if it is more restrictive, and similarly for the upper bound.
Quadratic Extensions¶
Knitro’s LP parser extends the standard format to support quadratic terms in both
the objective function and constraints. Quadratic expressions must be enclosed in
square brackets [ ]. A quadratic term is represented by either a squared
variable (e.g., x^2) or a product of two different variables (e.g., x*y)
with an associated coefficient (if the coefficient is 1, it can be omitted).
Optionally, a division operator can be added at the end of the square bracket
expression to indicate a potential division of the coefficients by a non-zero
constant, which can be useful if the quadratic matrix is given within a
particular convention.
Quadratic Objective¶
MINIMIZE
obj: x + 2 y + [ x^2 + 2 x*y + 3 y^2 ] / 2
Quadratic Constraints¶
SUBJECT TO
qc1: x + y + [ x^2 + 2 y^2 - x*y ] <= 10
Unsupported Features¶
The LP format can describe features that Knitro’s parser does not support. Including any of the following will result in a parsing error:
Special Ordered Sets (SOS)
Semi-continuous variables
Piecewise linear functions
Indicator or logical constraints
Non-linear functions beyond quadratic terms.
Parser Rules¶
Variable, Constraint, and Objective Names: Names are case-sensitive and must start with a letter. They can contain letters, digits, underscores, and the symbols
!#$%&()|~. Spaces and operators (-,+,*,/,^,=,>,<,;) are not allowed as they may interfere with parsing. When exporting, only the linear and quadratic components of the problem are written to the file; any general non-linear structures are omitted. Furthermore, if any variable, constraint, or objective names contain special characters (+-*/^=><;) or whitespace, these characters will be replaced with (@). If a variable does not have any name or its name is empty, Knitro will assign it a default name likex1,x2, etc. Similarly, unnamed constraints will be labeled asc1,c2, etc. The indexing of these default names is the same as the indexing used internally by Knitro.Numerical Values: Standard integer and floating-point numbers are supported, including scientific notation (e.g.,
1.5e-3). Infinity can be represented as+inf,-inf,+infinity, or-infinity.Comments: Use
\for single-line comments. For block comments, enclose the text between/*and*/.
\ This is a single-line comment
MINIMIZE
obj: x + y \ Minimize total cost
/* This is a block comment
spanning multiple lines */
Using LP Files in Knitro¶
Loading an LP File (C API)¶
Use the KN_read_problem function to load an LP file into a Knitro context.
/*---- LOAD LP FILE ----*/
if (KN_read_problem (kc, "problem.lp", NULL) != 0) {
printf("Error loading LP file\n");
exit(-1);
}
Writing an LP File (C API)¶
Use the KN_write_problem function to export the current problem in a Knitro context to the LP format.
/*---- WRITE LP FILE ----*/
if (KN_write_problem (kc, "output.lp", NULL) != 0) {
printf("Error writing LP file\n");
exit(-1);
}
MPS Format¶
Knitro implements a MPS (Mathematical Programming System) file reader to import optimization problems specified in MPS and extended MPS formats. Knitro’s parser uses by default the free format MPS-style, but supports as well the fixed MPS format.
Note that MPS files should be encoded as ASCII files.
To ensure that Knitro parses correctly the MPS file, the names of rows and columns should not have any blank spaces.
CORRECT:
name_variable
UNCORRECT:
name variable
The maximal length of a variable’s
name is set by default at 512 (the user can set the KN_MPS_LENGTH_NAME
option to change this setting).
Free MPS Format¶
Example¶
An example of a MPS file is given below:
NAME TESTPROB
ROWS
N COST
L LIM1
G LIM2
E MYEQN
COLUMNS
XONE COST 1 LIM1 1
XONE LIM2 1
YTWO COST 4 LIM1 1
YTWO MYEQN -1
ZTHREE COST 9 LIM2 1
ZTHREE MYEQN 1
RHS
RHS1 LIM1 5 LIM2 10
RHS1 MYEQN 7
BOUNDS
UP BND1 XONE 4
LO BND1 YTWO -1
UP BND1 YTWO 1
ENDATA
We discuss hereafter the different flags used in the (extended) free MPS format.
In the sequel, _ indicates a blank space.
NAME¶
Name of the problem. This section contains at most one line.
OBJSENSE (optional)¶
Sense of the objective function. This section contains at most one line with shape
SENSE
SENSE specifies the objective’s sense, with value being either
MAX
MIN
By default, the sense is set at MIN.
OBJNAME (optional)¶
Name of the objective. This section contains at most one line. By default, no name is set.
ROWS¶
In this section, each line specifies a row of the problem with shape
_S rowname
The S character specifies the sense of the current row,
with possible values being
E equality constraint
G greater than equal
L less than equal
N non specified
The objective line is specified by a N flag. If more than one line has
a N flag, the objective is assumed to be the first N flag encountered.
COLUMNS¶
Each line in this section specifies a column of the problem with shape
_cname1 rname1 value1 [rname2] [value2]
With
cname1 name of the variable corresponding to current row
rname1 name of a constraint where the row appears
value1 numerical values corresponding to row's coefficient in constraint
[rname2] name of a second constraint where the row appears
[value2] numerical values corresponding to row's coefficient in second constraint
Elements inside brackets [] are optional.
Note that rname1 and rname2 should be present in the ROWS section.
Columns’ names should be consecutive. Otherwise, the MPS file could not be parsed correctly.
CORRECT:
_cname1
_cname1
_cname2
UNCORRECT:
_cname1
_cname2
_cname1
RHS (optional)¶
This section specifies the right-hand side of the different constraints. Each line is shaped
_name cname1 value1 [cname2] [value2]
with
name name of the RHS vector
cname1 name of a constraint
value1 right-hand side of this constraint
[cname1] name of a second constraint
[value1] right-hand side of this second constraint
Elements inside brackets [] are optional.
cname1 and cname2 should be present in the ROWS section.
If a constraint cname presents in the ROWS section does not
appear in RHS, its right-hand side is set at 0 by default.
BOUNDS (optional)¶
This section specifies the upper and lower bounds for the variables
defined in the COLUMNS section. By default, if no bound is specified,
the lower bound LB is set equal to 0 and the upper bound UB is
set equal to KN_INFINITY.
Each line has the form
_BO vname value
with vname the name of the variable, BO the nature of the bounds,
defined as
FR Free variable
FX Fixed variable
LO Lower bound
UP Upper bound
MI Minus infinity
PL Plus infinity
If the same variable appears several times, additional values would be discarded.
Additional values exist to specify integer/binary variables:
BV Binary variable
UI Upper-bounded integer variable
LI Lower-bounded integer variable
RANGES (optional)¶
This section specifies constraints that lie inside an interval between two values.
A line inside the RANGES section has shape:
_T row1 value1 [row2] [value2]
with [row2] and [value2] optional values.
T is the right-hand side specifier.
We have the following possibilities used in the RHS section.
Row type |
Sign |
RHS lower limit |
RHS upper limit |
|---|---|---|---|
G |
+/- |
rhs |
rhs + range |
L |
+/- |
rhs - range |
rhs |
E |
+ |
rhs |
rhs + range |
E |
- |
rhs + range |
rhs |
For instance, the constraint
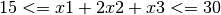
is encoded as
ROWS
L cons1
COLUMNS
x1 cons1 1
x2 cons1 2
x3 cons1 1
RHS
rhs cons1 30
RANGES
rhs cons1 15
QUADOBJ / QMATRIX (optional)¶
For quadratic structures in MPS there is not a single industry-wide standard. Knitro follows the most common implementation in this regard, shared with most other commercial solvers.
A quadratic objective function is specified either by a QUADOBJ flag
or a QMATRIX flag.
For each quadratic term, the format is
col1 col2 values
with col1 the name of the first variable and col2 the name
of the second variable, values being the coefficient of the term
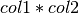 in the objective.
in the objective.
In QUADOBJ, diagonal terms (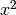 ) are doubled and off-diagonal
terms (
) are doubled and off-diagonal
terms (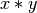 ) are written only once, in lower-triangular fashion.
In
) are written only once, in lower-triangular fashion.
In QMATRIX, diagonal terms are doubled and off-diagonal
terms are written twice, i.e. as a full symmetrical matrix.
For instance, the objective function
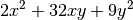
is encoded with QUADOBJ as
QUADOBJ
x x 4
y y 18
x y 32
and with QMATRIX as
QMATRIX
x x 4
y y 18
x y 32
y x 32
The term y * x is assumed implicit in QUADOBJ, thus explaining
why the term is not doubled.
The names x and y should be defined in the COLUMNS section.
QCMATRIX (optional)¶
Quadratic constraints are specified in QCMATRIX sections. Each quadratic
constraint qc_index is encoded by a dedicated QCMATRIX flag:
QCMATRIX qc_index
some text...
Inside a QCMATRIX flag, the format is similar as in
the QMATRIX section, that is, the format of each line is
col1 col2 values
with col1 the name of the first variable, col2 the name
of the second variable, values being the coefficient of the term
 in the constraint.
in the constraint.
The quadratic matrix  defined must be symmetric.
defined must be symmetric.
The constraint
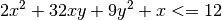
is encoded as
ROWS
L qc1
COLUMNS
x qc1 1
y qc1 0
QCMATRIX qc1
x x 2
y y 9
x y 16
y x 16
RHS
rhs1 qc1 12
ENDATA
For y to be defined correctly, it must appear in the COLUMNS section
even if it does not appear linearly in the qc1 constraint.
On the contrary of the QMATRIX and QUADOBJ section, no scaling
factor is applied to the definition of the constraint in the solver.
ENDATA (optional)¶
Specifies the end of the MPS file.
Loading MPS Files in Knitro¶
C API Example¶
In the callable library interface, a MPS file can be loaded through the KN_read_problem API function.
/*---- LOAD MPS FILE ----*/
if (KN_read_problem (kc, "file.mps", NULL) != 0)
exit( -1 );