Feasibility and infeasibility¶
This section deals with the issue of infeasibility or inability to converge to a feasible solution, and with options offered by Knitro to ensure that the iterates taken from the initial points to the solution remain feasible. This can be useful when, for instance, certain functions are not defined outside a given domain and the user wants to prevent the algorithm from evaluating these functions at certains points.
Infeasibility¶
Knitro is a solver for finding local solutions to general nonlinear, possibly non-convex problems. Just as Knitro may converge to a local solution that is not the global solution, it is also possible for a nonlinear optimization solver to converge to a locally infeasible point or infeasible stationary point on non-convex problems. That is, even if the user’s model is feasible, a nonlinear solver can converge to a point where the model is locally infeasible. At this point, a move in any direction will increase some measure of infeasibility and thus a local solver cannot make any further progress from such a point. Just as only a global optimization solver can guarantee that it will locate the globally optimal solution, only a global solver can also avoid the possibility of converging to these locally infeasible points.
If your problem is non-convex and the Knitro termination message indicates that it has converged to an infeasible point, then you should try running Knitro again from a different starting point (preferably one close to the feasible region). Alternatively, you can use the Knitro multi-start feature which will automatically try to run Knitro several times from different starting points, to try to avoid getting stuck at locally infeasible points.
If you are using one of the interior-point algorithms in Knitro, and Knitro
is struggling to find a feasible point, you can try different settings for the
bar_feasible user option to place special emphasis on obtaining
feasibility, as follows.
Feasibility options¶
Knitro offers an option bar_feasible that can force iterates
to stay feasible with respect to inequality constraints or can
place special emphasis on trying to get feasible.
If bar_feasible = 1 or bar_feasible = 3
Knitro will seek to generate iterates that satisfy the inequalities by
switching to a feasible mode
of operation, which alters the manner in which iterates are computed.
The option does not enforce feasibility with respect to equality constraints,
as this would impact performance too much.
In order to enter feasible mode, the initial point must satisfy all the inequalities to a sufficient degree; if not, Knitro may generate infeasible iterates and does not switch to the feasible mode until a sufficiently feasible point is found (with respect to the inequalities). We say sufficient satisfaction occurs at a point x if it is true for all inequalities that:
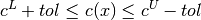
The constant tol>0 is determined by the option bar_feasmodetol;
its default value is 1.0e-4.
Feasible mode becomes active once an iterate x satisfies this condition
for all inequality constraints. If the initial point satisfies
this condition, then every iterate will be feasible with respect to the
inequalities.
Knitro can also place special emphasis on getting feasible
(with respect to all constraints) through the
option bar_feasible. If bar_feasible = 2
or bar_feasible = 3,
Knitro will first place special emphasis on getting feasible before working
on optimality. This option is not always guaranteed to accelerate the finding
of a feasible point. However, it may do a better job of obtaining feasibility
on difficult problems where the default version struggles.
The API function KN_set_con_honorbnds() can be used
to set the bar_feasible = 1 option individually for each
inequality constraint (as opposed to the global
bar_feasible option which applies to all inequality constraints). The settings
through this API function will override the setting through the global
bar_feasible user option.
Note
This option can only be used with the Interior/Direct and Interior/CG algorithms.
Honor bounds mode¶
In some applications, the user may want to enforce that the initial point and all subsequent iterates satisfy the simple bounds:
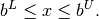
For instance, if the objective function or a nonlinear constraint function is undefined at points outside the bounds, then the bounds should be enforced at all times.
By default, Knitro makes an automatic choice about enforcing bounds on the variables.
Usually, by default, Knitro will choose to enforce bounds on the variables only for
the initial start point and the final solution (honorbnds = 2).
To enforce satisfaction at all iterates, set honorbnds = 1 (always).
To allow execution from an initial point that violates the bounds,
set honorbnds = 0 (no).
In addition, the API function KN_set_var_honorbnds() can be used
to set this option individually for each variable (as opposed to the global
honorbnds option which applies to all variables). The settings
through this API function will override the setting through the global
honorbnds user option.
Note
Note that setting honorbnds = 1 (always) or 2 (initpt) or using the default auto
option may cause Knitro to shift the value of a user-provided initial point so that it lies
sufficiently inside the (possibly presolved) bounds. Setting honorbnds = 0 (no)
will prevent Knitro from shifting a user-provided initial point.