Knitro / R reference

What is `KnitroR`?

KnitroR is the interface used to call Knitro from the R environment (requires R 3.0 or later).

KnitroR offers two routines to call Knitro from R:

knitro, which is an interface for the standard Knitro nonlinear and mixed-integer nonlinear optimizer
knitrolsq, which solves bound constrained nonlinear least-squares problems in vectorial format, that is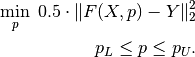

$\min_p \; 0.5\cdot\|F(X, p) - Y\|_2^2 \\ p_L \leq p \leq p_U.$

This type of fitting problems is ubiquitous in statistics and data analytics. This function is based on the internal Knitro implementation of nonlinear least-squares.

An important point when passing sparse matrices (parameters containing *Index*) to Knitro is that indices of the sparse matrix vectors must start from 0.

Syntax

The most elaborate form for general nonlinear programs is

res <- knitro(nvar=..., ncon=..., x0=...,
              objective=..., objGoal=..., gradient=..., gradientIndexVars=...,
              constraints=..., constraintsIndexCons,
              jacobian=..., jacIndexCons=..., jacIndexVars=...,
              hessianLag=..., hessIndexVars1=..., hessIndexVars2=...,
              callbackEvalFCGA=...,
              objLinearStruct=..., objLinearStructIndexVars=...,
              conLinearStruct=..., conLinearStructIndexCons=..., conLinearStructIndexVars=...,
              objQuadraticStruct=..., objQuadraticStructIndexVars1=..., objQuadraticStructIndexVars2=...,
              conQuadraticStruct=..., conQuadraticStructIndexCons=...,
              conQuadraticStructIndexVars1=..., conQuadraticStructIndexVars2=...,
              xL=..., xU=..., cL=..., cU=...,
              xTypes=..., xTypesIndexVars=...,
              xStrategies=..., xStrategiesIndexVars=...,
              xPriorities=..., xPrioritiesIndexVars=...,
              xHonorBnds=..., xHonorBndsIndexVars=...,
              ccTypes=..., ccIdxList1=..., ccIdxList2=...,
              objScaleFactor=..., xScaleFactors=..., xScaleCenters=...,
              cScaleFactors=..., ccScaleFactors=...,
              newptCallback=...,
              options=..., optionsFile=...,)

but the simplest function calls reduce to:

res <- knitro(objective=..., x0=...)
res <- knitro(objective=..., xL=...)
res <- knitro(objective=..., xU=...)
res <- knitro(nvar=..., objective=...)

You must provide the number of variables or one of the vector which KnitroR can use to infer it.
You must provide the number of constraints or one of the vector which KnitroR can use to infer it. Otherwise, KnitroR considers that the problem has no constraint.
You must provide an objective function for all terms which have not been added through objLinearStruct or objQuadraticStruct. If the objective is fully linear and quadratic and defined through these parameters, then it is not required to provide an objective function.
Similarly, if all constraints are linear and quadratic and have been defined through parameters conLinearStruct and conQuadraticStruct, then it is not required to provide a constraint function.
All other parameters are optional.
When a parameter among constraints, gradient, jacobian, hessianLag, xTypes, xStrategies, xPriorities is provided but the corresponding sparsity vectors (gradientIndexVars, jacIndexCons, jacIndexVars, hessIndexVars1, hessIndexVars2, …) are not, KnitroR consider them dense.
When a parameter among objLinearStruct, conLinearStruct, objQuadraticStruct, conQuadraticStruct is provided, it is required to provide the corresponding sparsity vectors.
KnitroR automatically switches to a mixed-integer nonlinear optimizer if the parameter xTypes is provided and defines at least one integer (1) or binary (2) variable.
An API for MPECs is also available via parameters ccTypes, ccIdxList1 and ccIdxList2.
Parameter callbackEvalFCGA can be used to evaluate the objective, the constraints, the gradient and the jacobian in the same callback. In this case, parameters objective, constraints, gradient and jacobian are ignored. See example fcga.R.

The API for bound constrained nonlinear least-squares problems has the following form :

res <- knitrolsq(dimp=..., par0=...,
                 dataFrameX=..., dataFrameY=...,
                 residual=...,
                 jacobian=..., jacIndexRsds=..., jacIndexVars=...,
                 rsdLinearStruct=..., rsdLinearStructIndexRsds=..., rsdLinearStructIndexVars=...,
                 parL=..., parU=...,
                 xScaleFactors=..., xScaleCenters=...,
                 objScaleFactor=....,
                 options=..., optionsFile=...)

Examples

rosenbrock.R: an NLP with no constraints. One example where it is only defined with the objective function. One example where it is defined with objective and gradient functions.
HS71.R: an NLP defined with objective, constraints, sparse jacobian and sparse hessianLag functions.
HS40.R: an NLP containing linear, quadratic and other nonlinear structures defined with objective, constraints, gradient, sparse jacobian and sparse hessianLag functions, and parameters objLinearStruct, conLinearStruct, objQuadraticStruct and conQuadraticStruct.
fcga.R: same problem as HS40.R, but the evaluation of the objective, the constraints and the first derivatives are computed in the same callback using callbackEvalFCGA.
lp1.R: an LP defined with parameters objLinearStruct and conLinearStruct. No objective or constraints function are provided.
QCQP1.R: an QCQP defined with the objective function and parameters objLinearStruct, conLinearStruct. objQuadraticStruct and conQuadraticStruct. The objective function is provided but not the constraints function.
multipleKnapsack.R: an ILP defined with parameters objLinearStruct and conLinearStruct. Variables are set integer with parameter xTypes. No objective or constraints function are provided.
minlp_case.R: a MINLP defined with objective, constraints, gradient, sparse jacobian and sparse hessianLag functions,
minlp_case_misqp.R: a MINLP solved with the MISQP algorithm,
minlp1.R: a MINLP using parameter constraintsIndexCons.
mpec1.R: an MPEC problem using parameter ccTypes.
lsq.R and lsfit.R: examples of knitrolsq usage.
mle.R: an example of maximum likelihood estimation with R and Knitro routines using different approaches.

Input Arguments of `knitro`

Below is a description of the input arguments of the knitro function of KnitroR.

Input Argument	Description
`nvar`	Number of variables.
`ncon`	Number of constraints.
`objective`	Objective function to be minimized or maximized. Prototype: `objective(x)` with `x` the current evaluation point. Output: the objective value at point `x`.
`objGoal`	Objective goal. `0` (default): minimize; `1`: maximize.
`gradient`	Gradient of the objective function. Prototype: `gradient(x)` with `x` the current evaluation point. Output: a vector containing the objective gradient values at point `x`.
`gradientIndexVars`	Vector containing the indices of the nonzero elements of the `gradient` function.
`constraints`	Nonlinear constraints function. Prototype: `constraints(x)` with `x` the current evaluation point. Output: a vector containing the constraints values at point `x`.
`constraintsIndexCons`	Vector containing the indices of the nonzero elements of the `constraints` function.
`jacobian`	Jacobian of nonlinear constraints function. Prototype: `jacobian(x)` with `x` the current evaluation point. Output: a vector containing the jacobian values at point `x`.
`jacIndexCons`	Vector containing the constraint indices of the nonzero elements of the `jacobian` function.
`jacIndexVars`	Vector containing the variable indices of the nonzero elements of the `jacobian` function.
`hessianLag`	Hessian function of Lagrangian. Prototype: `hessianLag(x, lambda, sigma)` with: `x` the current evaluation point. `lambda`: the current point dual variables/Lagrange multiplier `sigma`: scalar multiplier for the objective component Output: a vector containing the hessian values at point `x`.
`hessIndexVars1`	Vector containing the first variable indices of the nonzero elements of the `hessianLag` function.
`hessIndexVars2`	Vector containing the second variable indices of the nonzero elements of the `hessianLag` function.
`callbackEvalFCGA`	Function evaluating the objective, the constraints, the gradient and the jacobian. If set, then parameters `objective`, `constraints`, `gradient` and `jacobian` are ignored. Prototype: `callbackEvalFCGA(x)` with `x` the current evaluation point. Output: a list `(list(obj = obj, c = c, objGrad = objGrad, jac = jac))`.
`objLinearStruct`	Vector containing the coefficients of the linear terms of the objective.
`objLinearStructIndexVars`	Vector containing the variable indices of the linear terms of the objective.
`conLinearStruct`	Vector containing the coefficients of the linear terms of the constraints.
`conLinearStructIndexCons`	Vector containing the constraint indices of the linear terms of the constraints.
`conLinearStructIndexVars`	Vector containing the variable indices of the linear terms of the constraints.
`objQuadraticStruct`	Vector containing the coefficients of the quadratic terms of the objective.
`objQuadraticStructIndexVars1`	Vector containing the first variable indices of the quadratic terms of the objective.
`objQuadraticStructIndexVars2`	Vector containing the second variable indices of the quadratic terms of the objective.
`conQuadraticStruct`	Vector containing the coefficients of the quadratic terms of the constraints.
`conQuadraticStructIndexCons`	Vector containing the constraint indices of the quadratic terms of the constraints.
`conQuadraticStructIndexVars1`	Vector containing the first variable indices of the quadratic terms of the constraints.
`conQuadraticStructIndexVars2`	Vector containing the second variable indices of the quadratic terms of the constraints.
`x0`	Vector containing the initial guess.
`xL`	Vector containing the lower bounds of the variables.
`xU`	Vector containing the upper bounds of the variables.
`cL`	Vector containing the lower bounds of the constraints.
`cU`	Vector containing the upper bounds of the constraints.
`xTypes`	Vector containing the types of the variables. `0`: continuous; `1`: integer; `2`: binary.
`xTypesIndexVars`	Vector containing the indices of the nonzero elements of parameters `xTypes`.
`xStrategies`	Vector containing the strategies for dealing with individual integer variables. `0`: default; `1`: relax; `2`: mpec (binary variables only).
`xStrategiesIndexVars`	Vector containing the indices of the nonzero elements of parameter `xStrategies`.
`xPriorities`	Vector containing the branching priorities for integer variables. Values for continuous variables are ignored.
`xPrioritiesIndexVars`	Vector containing the indices of the nonzero elements of parameter `xPriorities`.
`xHonorBnds`	Vector containing the `KN_PARAM_HONOBNDS` values for individual variables.
`xHonorBndsIndexVars`	Vector containing the indices of the nonzero elements of parameter `xHonorBnds`.
`ccTypes`	Vector containing the types of the complementarity constraints. `0`: two (non-negative) variables; `1`: a variable and a constraint (not supported yet); `2`: two constraints (not supported yet);
`ccIdxList1`	Vector containing the first indices of the complementarity constraints.
`ccIdxList2`	Vector containing the second indices of the complementarity constraints.
`xScaleFactors`	Vector containing the scaling factors of the variables.
`xScaleCenters`	Vector containing the scaling centers of the variables.
`cScaleFactors`	Vector containing scaling factors of the nonlinear constraints.
`ccScaleFactors`	Vector containing scaling factors of the complementarity constraints.
`objScaleFactor`	Scaling factor of the objective function.
`options`	Options stored as an R list. Example: `options <- list("outlev" = 0, "derivcheck" = 2))`. See Knitro user options for the list of available options.
`optionsFile`	Options stored in a file.

Input Arguments for `knitrolsq`

Below is a descriptions of the API of the R function knitrolsq in KnitroR. The function knitrolsq is based on Knitro’s internal implementation of bound-constrained nonlinear least-squares.

Input Argument	Description
`dimp`	Dimension of fitting parameter.
`par0`	Initial guess on fitting parameter.
`dataFrameX`	Data frame containing samples x_i.
`dataFrameY`	Data frame containing samples y_i.
`residual`	Nonlinear least-squares residual function. Prototype: `residual(p, dfX, dfY)` with: `p`: current evaluation point. `dfX`, `dfY`: data frames passed through `dataFrameX` and `dataFrameY`. Ouput: vector containing the residual values at point `p`.
`jacobian`	Jacobian of nonlinear least-squares residuals. Prototype: `jacobian(x)` with `x` the current evaluation point. Output: a vector containing the jacobian values at point `x`.
`jacIndexRsds`	Vector containing the residual indices of the nonzero elements of the residual `jacobian` function.
`jacIndexVars`	Vector containing the variable indices of the nonzero elements of the residual `jacobian` function.
`rsdLinearStruct`	Vector containing the coefficients of the linear terms of the residuals.
`rsdLinearStructIndexRsds`	Vector containing the residual indices of the linear terms of the residuals.
`rsdLinearStructIndexVars`	Vector containing the variable indices of the linear terms of the residuals.
`parL`	Vector of lower bounds on fitting parameter (R vector).
`parU`	Vector of upper bounds on fitting parameter (R vector).
`xScaleCenters`	Vector of scaling centers on fitting parameter. (R vector).
`xScaleFactors`	Vector of scaling factors on fitting parameter. (R vector).
`objScaleFactor`	Scaling factor on nonlienar least-squares objective function.
`options`	Options stored as an R list. Example: `options <- list("outlev" = 0, "derivcheck" = 2))`. See Knitro user options for the list of available options.
`optionsFile`	Options stored in a file.

Output Arguments of `knitro` and `knitrolsq`

Output Argument	Description
`status`	Knitro’s status.
`obj`	Objective value.
`x`	Vector containing the variable primal values.
`lambda`	Vector containing the variable dual values.
`objGrad`	Vector containing the objective gradient values.
`objGradIndexVars`	Vector containing the indices of the nonzero elements of `objGrad`.
`c`	Vector containing the constraint values.
`r`	Vector containing the residual function values (LSQ only).
`jac`	Vector containing the Jacobian values.
`jacIndexCons`	Vector containing the constraint indices of the nonzero elements of `jac`.
`jacIndexVars`	Vector containing the variable indices of the nonzero elements of `jac`.
`rsdJac`	Vector containing the residual Jacobian values (LSQ only).
`rsdJacIndexCons`	Vector containing the constraint indices of the nonzero elements of `rsdJac`.
`rsdJjacIndexVars`	Vector containing the variable indices of the nonzero elements of `rsdJac`.
`numFCevals`	Number of objective evaluations.
`numGAevals`	Number of gradient evaluations.
`numHevals`	Number of Hessian evaluations.
`numHVevals`	Number of Hessian-vector product evaluations.
`numIters`	Number of iterations (continuous models only).
`numCGiters`	Number of conjugate gradient iterations (continuous models only).

Knitro / R reference

What is KnitroR?

Syntax

Examples

Input Arguments of knitro

Input Arguments for knitrolsq

Output Arguments of knitro and knitrolsq

What is `KnitroR`?

Input Arguments of `knitro`

Input Arguments for `knitrolsq`

Output Arguments of `knitro` and `knitrolsq`