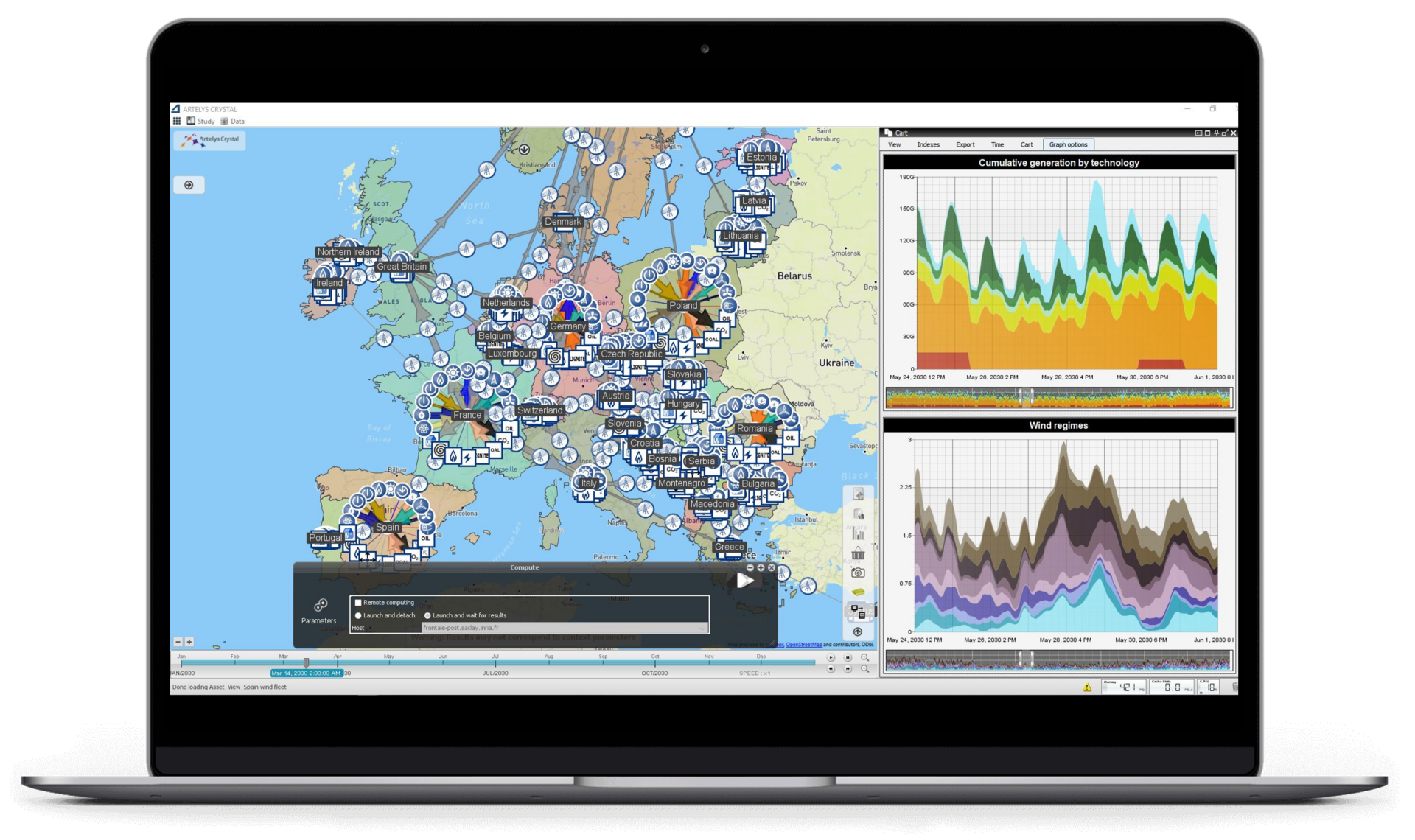
— Artelys Crystal Super Grid fournit les éléments quantitatifs qui permettent d’évaluer les coûts et bénéfices d’une stratégie énergétique et de l’optimiser.
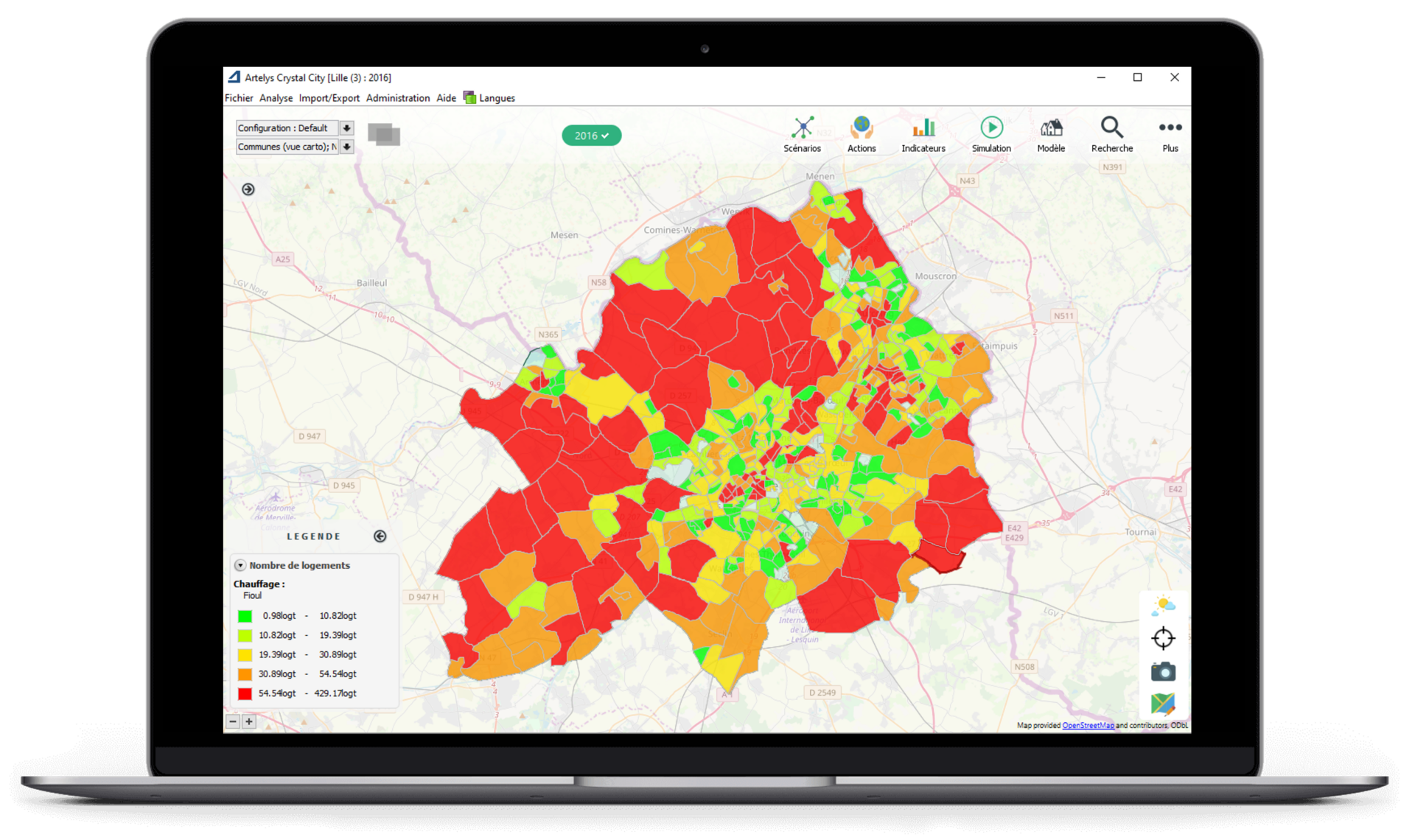
— Artelys Crystal City est l’outil de référence pour la planification énergétique territoriale. Son interface intuitive et ses fonctions avancées en font le chef d’orchestre idéal pour mener à bien la transition énergétique dans les territoires.
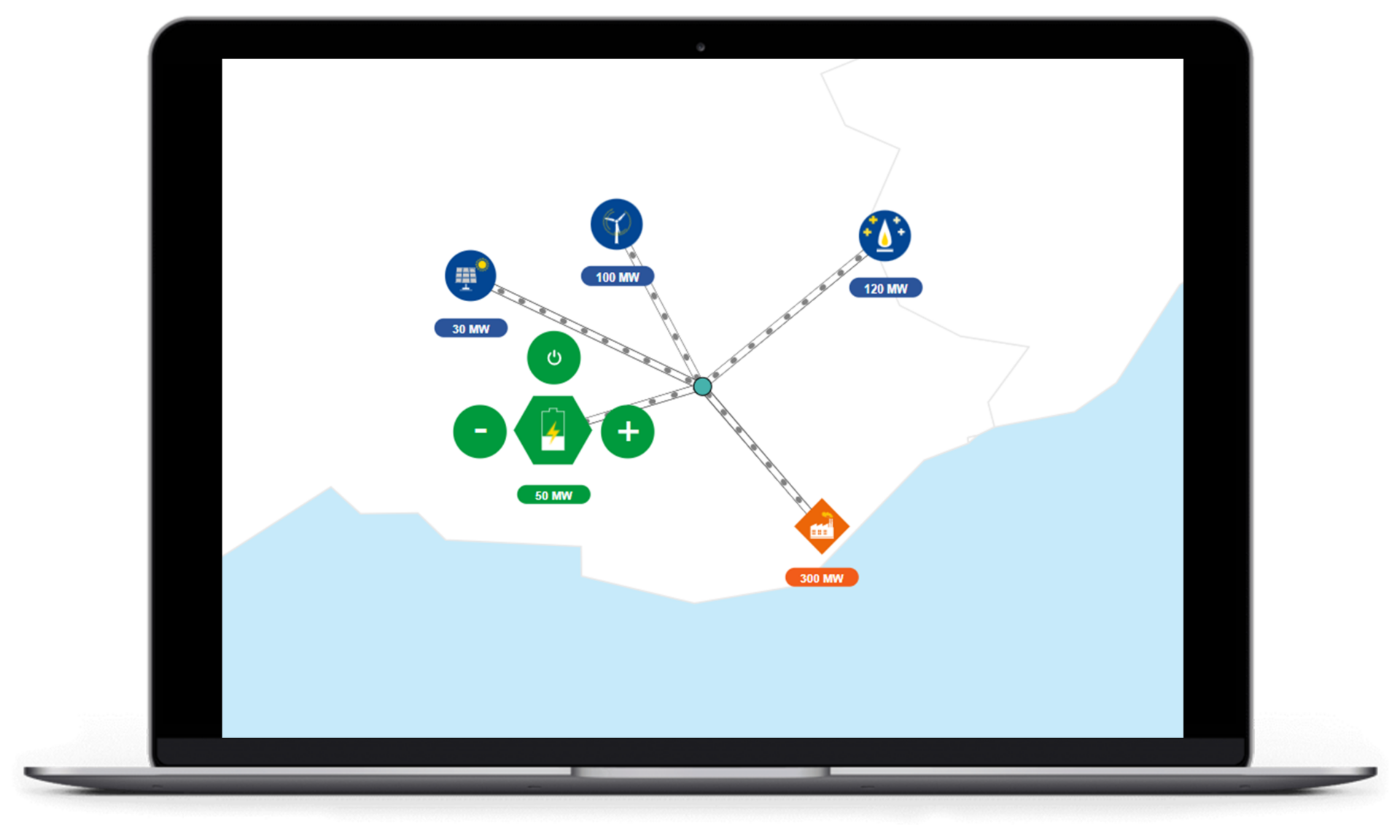

— Artelys Crystal Energy Explorer est l’outil idéal pour vous permettre d’appréhender et de communiquer en interne et en externe sur les défis relatifs à la gestion des infrastructures électriques, gazières et hydrogènes.
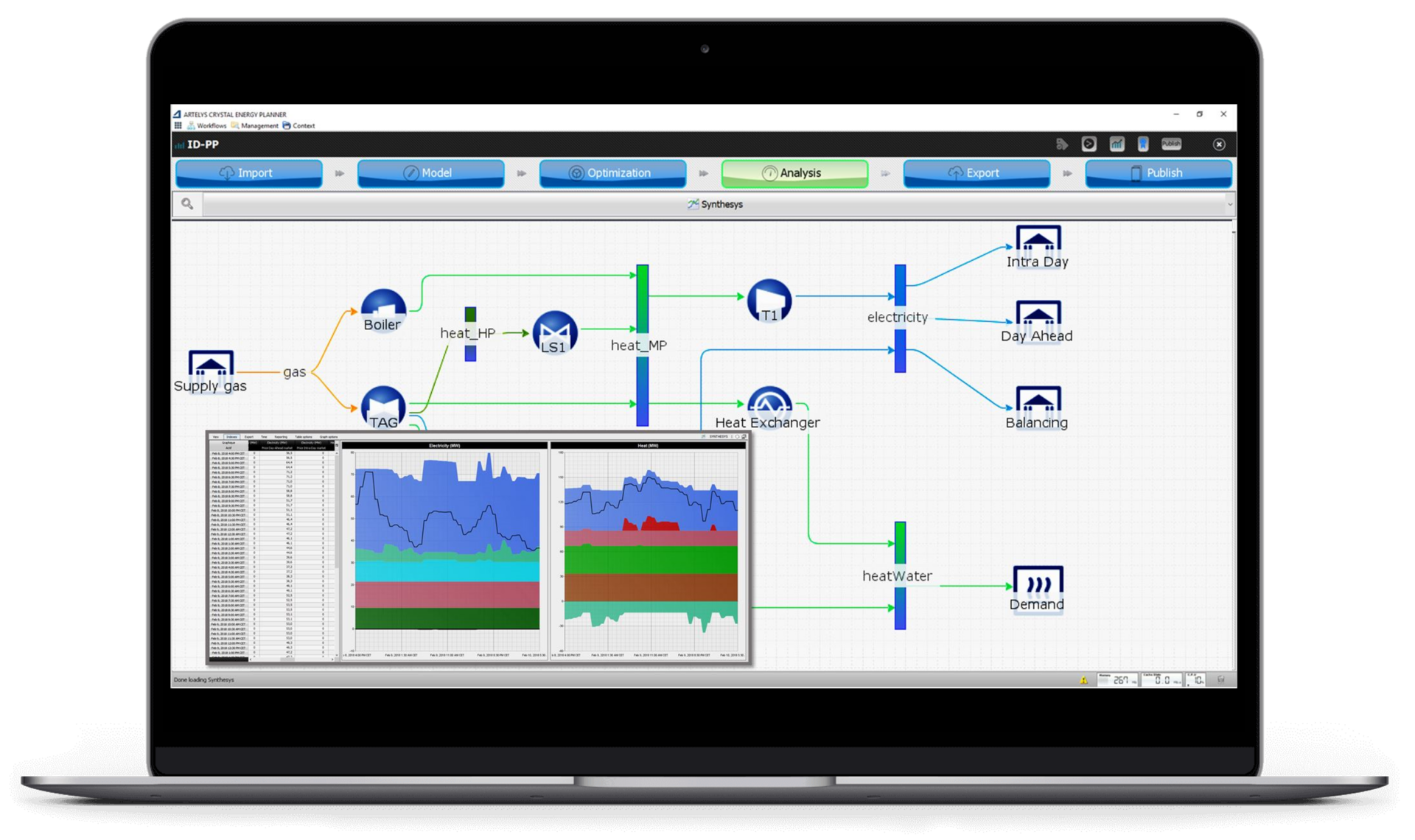
— Artelys Crystal Energy Planner optimise la gestion opérationnelle à court et moyen terme des actifs de production énergétique. La planification opérationnelle, ainsi simplifiée et fiabilisée, devient plus compétitive.
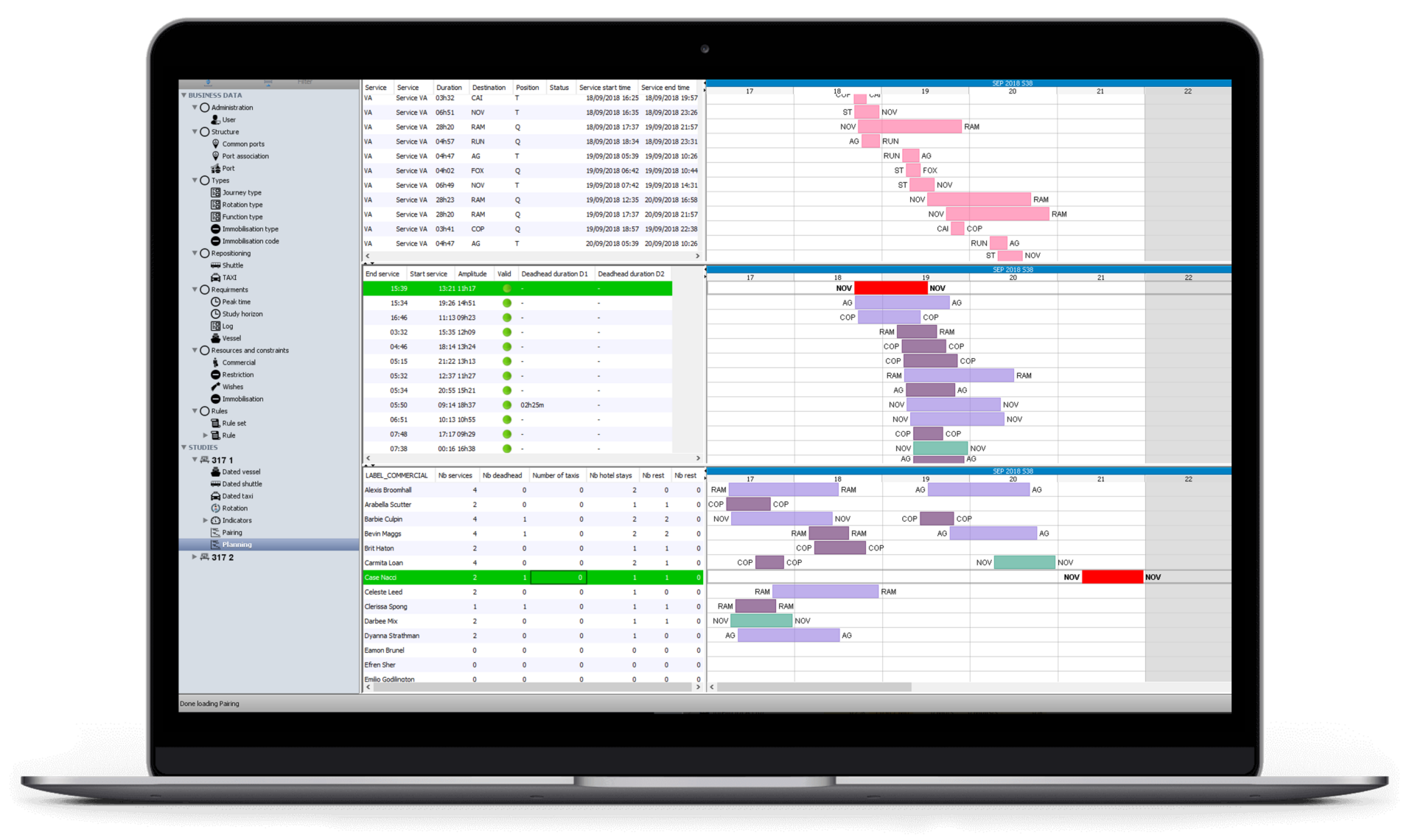
— La planification des ressources est une question centrale pour les entreprises afin d’améliorer la gestion des coûts, la productivité et la qualité de service pour le client final.
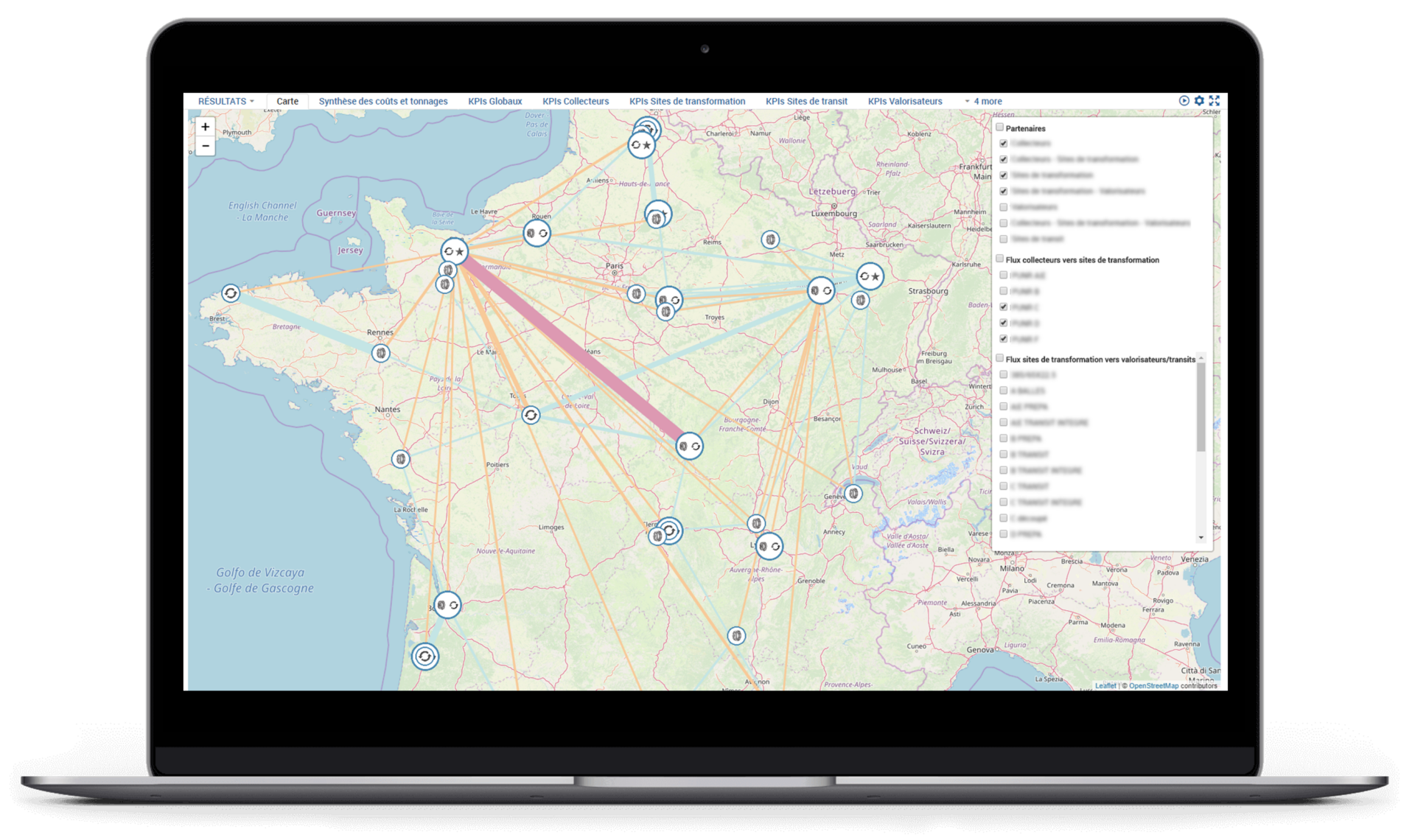
— Artelys Crystal Network Designer est une solution logicielle dédiée à l’optimisation, au dimensionnement et à l’analyse de réseaux logistiques. Elle vous permet de réduire vos coûts logistiques dans leur ensemble, d’anticiper et de piloter vos flux à différents horizons ainsi que de simuler des scénarios sur votre réseau : du redimensionnement à l’aléa opérationnel.

— A l’heure de la transition énergétique, les décideurs locaux se trouvent confrontés à de nouveaux enjeux de planification territoriale, la dimension énergétique devenant un facteur clé dans la prise de décision.

— Artelys Crystal Super Grid fournit les éléments quantitatifs qui permettent d’évaluer les coûts et bénéfices d’une stratégie énergétique et de l’optimiser.

— Artelys Crystal Energy Planner optimise la gestion opérationnelle à court et moyen terme des actifs de production énergétique. La planification opérationnelle, ainsi simplifiée et fiabilisée, devient plus compétitive.

—La planification des ressources est une question centrale pour les entreprises afin d’améliorer la gestion des coûts, la productivité et la qualité de service pour le client final.

— Artelys Crystal Network Designer est une solution logicielle dédiée à l’optimisation, au dimensionnement et à l’analyse de réseaux logistiques. Elle vous permet de réduire vos coûts logistiques dans leur ensemble, d’anticiper et de piloter vos flux à différents horizons ainsi que de simuler des scénarios sur votre réseau : du redimensionnement à l’aléa opérationnel.

— A l’heure de la transition énergétique, les décideurs locaux se trouvent confrontés à de nouveaux enjeux de planification territoriale, la dimension énergétique devenant un facteur clé dans la prise de décision.

— Artelys Crystal Super Grid fournit les éléments quantitatifs qui permettent d’évaluer les coûts et bénéfices d’une stratégie énergétique et de l’optimiser.

— Artelys Crystal Energy Planner optimise la gestion opérationnelle à court et moyen terme des actifs de production énergétique. La planification opérationnelle, ainsi simplifiée et fiabilisée, devient plus compétitive.

— La planification des ressources est une question centrale pour les entreprises afin d’améliorer la gestion des coûts, la productivité et la qualité de service pour le client final.

— Artelys Crystal Network Designer est une solution logicielle dédiée à l’optimisation, au dimensionnement et à l’analyse de réseaux logistiques. Elle vous permet de réduire vos coûts logistiques dans leur ensemble, d’anticiper et de piloter vos flux à différents horizons ainsi que de simuler des scénarios sur votre réseau : du redimensionnement à l’aléa opérationnel.
| Cookie | Description |
|---|---|
| cookielawinfo-checkbox-analytics | Ce cookie enregistre le consentement de l'utilisateur pour les cookies de la catégorie "Analytics". |
| CookieLawInfoConsent | Ce cookie est défini pour enregistrer l'état du bouton par défaut de la catégorie correspondante et le statut du CCPA. Il ne fonctionne qu'en coordination avec le cookie principal. |
| PHPSESSID | Ce cookie est natif des applications PHP. Il stocke et identifie l'identifiant de session unique d'un utilisateur afin de gérer les sessions des utilisateurs sur le site web. Il s'agit d'un cookie de session qui sera supprimé lorsque toutes les fenêtres du navigateur seront fermées. |
| viewed_cookie_policy | Le cookie est utilisé pour indiquer si l'utilisateur a consenti ou non à l'utilisation de cookies. Il ne stocke aucune donnée personnelle. |
| Cookie | Description |
|---|---|
| _ga | Utilisé pour distinguer les utilisateurs. |
| _gat | Utilisé pour limiter le taux de requête de Google Analytics. |
| _gid | Utilisé pour distinguer les utilisateurs. |
| Cookie | Description |
|---|---|
| pll_language | Polylang utilise ce cookie pour se souvenir de la langue choisie par l'utilisateur lorsqu'il revient sur le site web et pour obtenir des informations sur la langue lorsqu'elles ne sont pas disponibles d'une autre manière. |