Product overview¶
Artelys Knitro is an optimization software library for finding solutions of both continuous (smooth) optimization models (with or without constraints), as well as discrete optimization models with integer or binary variables (i.e. mixed integer programs). Knitro is primarily designed for finding local optimal solutions of large-scale, continuous nonlinear problems.
The problems solved by Knitro have the form
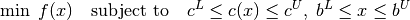
where 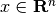 are the unknown variables (which can be specified as
continuous, binary or integer),
are the unknown variables (which can be specified as
continuous, binary or integer), 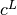 and
and 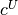 are lower and upper bounds
(possibly infinite) on the general constraints, and
are lower and upper bounds
(possibly infinite) on the general constraints, and 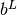 and
and 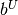 are lower and upper simple bounds (possibly infinite) on the variables.
This formulation allows many types of constraints, including equalities
(if
are lower and upper simple bounds (possibly infinite) on the variables.
This formulation allows many types of constraints, including equalities
(if 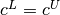 ), fixed variables (if
), fixed variables (if 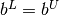 ), and both
single and double-sided inequality constraints or bounded variables.
Complementarity constraints may also be included.
Knitro assumes that the functions
), and both
single and double-sided inequality constraints or bounded variables.
Complementarity constraints may also be included.
Knitro assumes that the functions 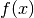 , and
, and 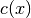 are smooth,
although problems with derivative discontinuities can often be solved
successfully.
are smooth,
although problems with derivative discontinuities can often be solved
successfully.
Although primarily designed for general, nonlinear optimization, Knitro is efficient at solving all of the following classes of optimization problems (described in more detail in Section Special problem classes):
unconstrained;
bound constrained;
systems of nonlinear equations;
least squares problems, both linear and nonlinear;
linear programming problems (LPs);
quadratic programming problems (QPs), both convex and non-convex;
quadratically constrained quadratic programs (QCQPs);
second order cone programs (SOCPs)
mathematical programs with complementarity constraints (MPCCs);
general nonlinear (smooth) constrained problems (NLP), both convex and non-convex;
mixed integer linear programs (MILP) of moderate size;
mixed integer (convex) nonlinear programs (MINLP) of moderate size;
derivative free (DFO) or black-box optimization.
The Knitro package provides the following features:
efficient and robust solution of small or large problems;
solvers for both continuous and discrete problems;
derivative-free, 1st derivative, and 2nd derivative options;
option to remain feasible throughout the optimization or not;
multi-start heuristics for trying to locate the global solution;
both interior-point (barrier) and active-set methods;
both iterative and direct approaches for computing steps;
support for Windows (64-bit), Linux (64-bit) and Mac OS X (64-bit);
programmatic interfaces: C, C++, C#, Fortran, Java, Julia, Python, R;
modeling language interfaces: AMPL ©, AIMMS ©, GAMS ©, MATLAB ©, MPL ©, Microsoft Excel Premium Solver ©;
thread-safe libraries for easy embedding into application software;
a specialized API for bound-constrained nonlinear least-squares problems.